Принятие или отвержение нуль-гипотезы

Вычисление F-отношения

Теперь у нас есть четыре оценки популяционной дисперсии σ̅² _X. Это (1) внутригрупповое среднее квадратичное; (2) среднее квадратичное по строкам; (3) среднее квадратичное но столбцам и (4) среднее квадратичное – строки×столбцы. Мы можем использовать внутригрупповое среднее квадратичное как -знаменатель при вычислении F-отношения относительно каждого из остальных средних квадратичных. Введение знаменателя часто называют показателем ошибки, имея в виду несистематическое изменение, которое невозможно контролировать в экспериментальных условиях:

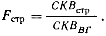(8.13)

В нашем случае

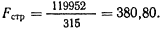
Таким же образом,

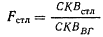(8.14)

или:

И еще раз соответственно:

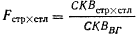(8.15)

или:

Аналогично тому, как это делалось в статистическом приложении к главе 7, мы воспользуемся Статистической таблицей 3 для нахождения критического Значения F. Для F_стр имеется 1 df в числителе и 64 df в знаменателе. Табличное значение для отвержения нуль-гипотезы для 1 и 65 df равно 7,04 на уровне 0,01, Очевидно, что полученная нами величина 380,80 позволяет на этом уровне отклонить нуль-гипотезу. Для F_стр комбинация в числителе и знаменателе та же самая. И здесь полученная величина 19,48 позволяет отклонить нуль-гипотезу на альфа-уровне, равном 0,01.

Для Fстр×стл мы также ищем табличное значение для 1 и 65 df. Полученная нами величина 0,86 не позволяет отклонить нуль-гипотезу даже для альфа-уров-ня = 0,05. Критическое значение здесь равно 3,99. F, меньшее единицы, может быть получено лишь для выборочного распределения. В этом случае оно просто не может быть статистически значимым.

Таблица дисперсионного анализа

Дисперсионный анализ можно подытожить в виде следующей таблицы. Обратите внимание, что степени свободы являются аддитивными так же, как и суммы квадратов.

Дисперсионный анализ.

Эксперимент на время реакции

с разными типами стимулов и видами реакций

Источник дисперсии	СК	df	СКВ	F	p
Реакции (строки)				380,80	<0,01
Стимулы (столбцы)				19,48	<0,01
Взаимодействие строки × столбцы				0,86
Внутрнгрупповая
Общая

Задача. Используйте данные из задачи в статистическом приложении к главе 7 и проведите дисперсионный анализ с составлением таблицы дисперсионного анализа. Снова данные получены для шести раздельных групп испытуемых. Одной переменной является величина награды, второй переменной – трудность задачи. Данные из главы 7 должны быть использованы следующим образом.

Трудность	Величина награды от низкой к высокой ·
А	Б	в
Легкая Трудная	Ур. 4 Ур. 3	Ур. 5 Ур. 2	Ур. 6 Ур. 1
Ответ:

Источник дисперсии	СК	df	СКВ	F	p
Трудность (строки)	433,2		433,2	46,33	<0,01
Награда (столбцы)	15,8		7,9	0,84
Взаимодействие (трудность ×награда)	141,8		70,9	7,58	<0,01
Внутригрупповая	224,4		9,35
Общая	815,2

Глава 9. КОРРЕЛЯЦИОННЫЕ ИССЛЕДОВАНИЯ

Дата добавления: 2015-05-26