Метод ітерацій

Лекція 4. МЕТОДИ РОЗВ‘ЯЗУВАННЯ СИСТЕМ НЕЛІНІЙНИХ РІВНЯНЬ

На відміну від систем лінійних рівнянь не існує прямих методів розв‘язання систем нелінійних рівнянь (СНР) загального виду. Для наближеного їх розв‘язання використовують ітераційні методи. Найбільш поширеними з них є метод ітерацій і метод Ньютона.

Метод ітерацій для СНР по суті є узагальненням методу ітерацій для одного рівняння.

Нехай для обчислення невідомих х₁, х₂, …, х_n необхідно розв‘язати систему

n нелінійних рівнянь

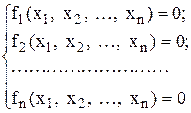(4.1)

Зобразимо систему (4.1) у вигляді

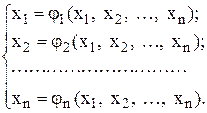(4.2)

Функції 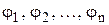в (4.2) поблизу шуканого розв‘язку мають задовольняти умові збіжності методу ітерацій, яка записується наступнім чином

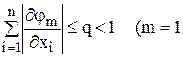, або 2, …, або n) (4.3)

(фактично узагальнена умова для одного рівняння).

Задаються початковим наближенням 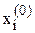, і = 1, 2, …, n.

Взагалі, необхідно, щоб початкове наближення було достатньо близько до шуканого розв‘язку. Вибір наближення провадиться в залежності від конкретних умов, наприклад, з фізичних міркувань. Якщо розв‘язується система із двох рівнянь, то за 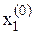, 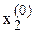можна прийняти координати точки перетину кривих 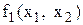і 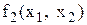на площині .

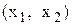Наступні наближення визначають за ітераційними формулами

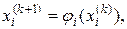k = 0, 1, 2, … (4.4)

Ітераційний процес завершується при виконанні умови

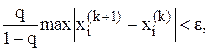(4.5)

де ε – задана абсолютна похибка розв‘язку.

Одним із суттєвих недоліків методу ітерацій є складність вибору функцій 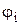такими, що задовольняють достатній умові збіжності ітераційного процесу. Для системи із двох рівнянь можна рекомендувати наступний засіб (А).

Записують 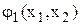і 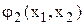у вигляді

;

,

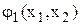
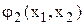
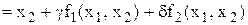де .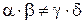

Коефіцієнти 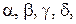визначають із умов:

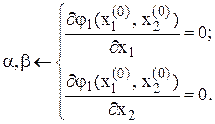
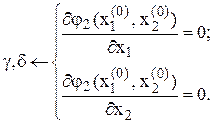(4.6)

Умова збіжності при цьому виконується, якщо 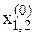прийняті достатньо близько до шуканого розв‘язку.

Для СНР, як і для СЛАР, можливе застосування удосконалення Зейделя, тобто використання раніше визначених невідомих при обчисленні наступних. Власне, для СНР методом ітерацій і називають метод Зейделя.

Дата добавления: 2015-05-26