Лекция 9. Гамма-излучение ядер

Гамма-излучением называется электромагнитное излучение, возникающее при переходе атомных ядер из возбужденных состояний в состояния с меньшей энергией. В таких процессах числа протонов и нейтронов в ядре не изменяются, а испускаются γ-кванты: фотоны с энергией от 10 кэВ до 5 МэВ. Изолированный свободный нуклон (как и свободный электрон) не может испускать γ-кванты без нарушения законов сохранения энергии и импульса. Однако такой процесс становится возможным в ядре, поскольку испускаемый γ-квант способен обмениваться импульсом со всеми остальными нуклонами. Спектр γ-излучения всегда дискретный, т.к. дискретны энергетические уровни самого ядра.

С точностью до незначительной энергии ядра отдачи энергия γ-кванта равна разности энергий соответствующих ядерных уровней Δ Е. Ядерные уровни характеризуются определенными значениями спина J и четности P. Поэтому, изучая γ-спектры, можно получить информацию о ядерных уровнях.

9.1. Классификация фотонов. К фотону неприменимо определение спина как момента покоящейся частицы, поскольку для фотона, всегда движущегося со скоростью света, вообще не существует системы координат, в которой его можно было бы рассматривать как покоящийся (постулат релятивистской механики). Отсюда следует, что для фотона не существует и понятия орбитального момента, т.к. возможность разделить спин и орбитальный момент требует независимости координатной и спиновой части волновой функции:

.

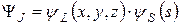(для частицы с ненулевой массой покоя разделение всегда возможно). В случае фотона можно говорить лишь о его полном угловом моменте J. Тем не менее, хотя разделение момента фотона на орбитальный момент и спин лишено физического смысла, удобно ввести «спин» S и «орбитальный момент» L формальным образом: как вспомогательные понятия, выражающие свойства преобразования волновой функции по отношению к вращениям. При этом свойства электромагнитного поля показывают, что для фотона S = 1, а внутренняя четность равна –1. Поэтому четность фотона с орбитальным числом l будет

.

Поскольку спиновое число фотона S может принимать значения +1, 0 или –1, полный момент j будет равен соответственно l + 1, l и l – 1. Таким образом, для фотонов с определенным l имеем разные j и, следовательно, разные четности, а именно, возможны состояния фотона с четностью

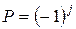и .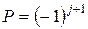

Первые называют фотонами электрического, а вторые – магнитного типа.

Вместо понятия орбитального момента для фотона используется аналог, называемый мультиполем. Мультиполь – это состояние фотона с определенными значениями полного углового момента j и четности P. Состояние с угловым моментом j и четностью (–1) ^j называется электрическим 2 ^j -полем, а с моментом j и четностью (–1) ^{j +1} – магнитным 2 ^j -полем. Состояния j = 1 называются диполями, j = 2 квадруполями, j = 3 октуполями, и т.д. Для обозначения кванта электрического мультиполя используется буква Е, магнитного – М, т.е. пишут, например, Е1 – электрический диполь, М1 – магнитный диполь, Е2 – электрический квадруполь и т.д. (табл. 9.1). Мультипольная терминология основана на классическом понятии мультиполя как системы зарядов, обладающей определенной симметрией (см. п. 4.4). Так, при колебаниях электрического диполя возникает излучение, которое с квантовой точки зрения состоит из Е1 фотонов.

Таблица 9.1.

Мультиполи и их четность

	Электрические (Е), l = j – 1	Магнитные (М), l = j
j=	P= (–1) ^j	P= (–1) ^j+1
1 (диполь)	–1	+1
2 (квадруполь)	+1	–1
3 (октуполь)	–1	+1
4 (гексадекуполь)	+1	–1

Можно показать, что вероятность испускания (а также поглощения) γ-кванта ядром определяется его мультипольностью. Будем, для примера, рассматривать падение γ-кванта на ядро. γ-квант, летящий не точно на центр ядра, т.е. имеющий орбитальный момент l ≠ 0, испытывает влияние центробежного потенциала (7.17). При достижении расстояния r до центра ядра, определяемого равенством U_ц = E _γ, под действием центробежной силы фотон должен был бы рассеяться в обратном направлении. Вероятность оказаться на поверхности ядра (т.е. на расстоянии R от центра) определяется, таким образом, вероятностью туннельного эффекта. Для расчета последней используем формулу (7.12), полученную при рассмотрении прохождения частиц через потенциальный барьер произвольной формы. Тогда

.

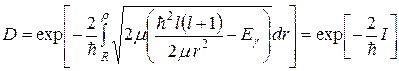Воспользуемся далее тем, что для фотона 2 μс ²= E _γ.[81] Избавившись, таким образом, от приведенной массы и выполнив замены

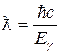и ,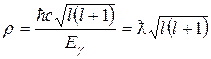

приведем I к виду, удобному для интегрирования:

Так как длина волны фотона в нашем случае ~ 10^-13–10^{-10 м, а радиус ядра R ~ 10-15}–10^{-14 м, для γ-квантов выполняется условие длинноволнового приближения, и} r >> R. Это дает

.

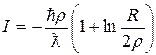Таким образом, вероятность преодолеть центробежный потенциал и достичь ядра определяется для фотона выражением[82]

.

Переходя от коэффициента прозрачности к постоянным распада γ-активных ядер (ср. п. 7.3), найдем, что для испускания 2 ^j -полей электрического типа

. (9.1)

Вероятность распада с испусканием 2 ^j -полей магнитного типа

. (9.2)

Для γ-излучения ядер стоящее в скобках отношение заметно меньше единицы (длинные волны). Это приводит к тому, что ядра испускают преимущественно фотоны низшей мультипольности, разрешенной законами сохранения момента и четности. Наиболее вероятным является электрический дипольный переход, или Е1. За ним в порядке убывания вероятности следуют М1 ≈ Е2 > М2 ≈ Е3, и т.д. Увеличение степени мультипольности уменьшает вероятность излучения в отношении . В силу (9.1) и (9.2) λ пропорциональна (E_γ)^{2 j –1} или (E_γ)^{2 j}.

Мультипольность каждого конкретного перехода определяется моментами и четностями начального и конечного состояния ядра. Законы сохранения требуют, чтобы выполнялись равенства

,

.

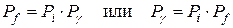Абсолютно запрещены т.н. 0-0 переходы, когда момент начального и конечного состояния ядра равен нулю. Действительно, в этом случае γ-квант должен уносить момент равный 0, однако состояний фотона с j = 0 не существует из-за поперечности электромагнитных волн.

9.2. Каскадное испускание γ-квантов. Переход ядра из возбужденного состояние в основное при γ-излучении может быть однократным, но может быть и каскадным, если он осуществляется в результате последовательного испускания нескольких γ-квантов. Типичный пример – ²⁴Na (рис. 9.1). Основное его состояние имеет характеристику 4+. В результате β-распада образуется ядро ²⁴Mg. Однако это ядро не получается сразу в основном состоянии, так как последнее имеет характеристику 0+. Однако имеются два доступных возбужденных уровня (Е_возб = 1,37 и 4,12 МэВ) с характеристиками 2+ и 4+. Переход на первый из них путем β-распада также запрещен по спину, хотя и не так сильно, как на основной уровень. β-распад (с периодом полураспада 15 часов) идет, главным образом, на уровень 4,12 МэВ: 4+ → 4+.[83] С этого уровня происходит испускание γ-кванта (4+ → 2+) и переход на уровень 1,37 МэВ. Разрешенные при этом значения момента γ-кванта j – от 2 до 6, а его четность положительна. Поэтому наиболее вероятно испускание квадруполей электрического типа Е2 с энергией 2,75 МэВ. Намного менее вероятны Е4 и М3 (и практически невероятны Е6 и М5). Переход на основной уровень (2+ → 0+) требует j = 2 и положительной четности, т.е. также происходит испускание фотона Е2 с энергией 1,37 МэВ. Заметим, что переход (4+ → 0+) требует Е4 и поэтому гораздо менее вероятен.[84]

9.3. Ядерная изомерия. Среднее время жизни возбужденных состояний ядер чаще всего невелико (порядка 10^–11–10^–7 с). Однако в некоторых случаях, при сочетании высокой степени запрета с малой разницей в энергии соответствующих уровней ядра, могут образоваться долгоживущие γ-активные ядра с периодом полураспада макроскопического масштаба: до нескольких часов и больше (так, период полураспада ^{186 m} Re равен 2∙10⁵ лет). Такие долгоживущие метастабильные состояния ядра называются изомерами. [85] Явление ядерной изомерии было открыто в 1921 г. О. Ганом. Он обнаружил, что при β-распаде ²³⁴Th получаются два радиоактивных нуклида (ториевая «вилка»), которые состоят из одинаковых ядер ²³⁴Pa, но имеют различные периоды полураспада: 6,7 ч и 1,22 мин.

Пример ²³⁴Pa долгое время оставался единственным. Однако в 1935 г. другой случай ядерной изомерии (у искусственно полученного изотопа ⁸⁰Br) был открыт И.В. Курчатовым и др. Позже было найдено большое количество других пар, а также троек изомерных ядер[86] (всего более трехсот). Из-за сравнительно большого времени жизни изомер фактически проявляет свойства нового ядра: с другим значением массы (энергии), спина, четности, периода полураспада, со своей схемой распада, но с теми же самыми А и Z. Достаточно долгоживущий изомер может быть химическим путем отделен от материнского радионуклида и далее использоваться независимо.[87] Объяснение природы изомерии существованием у ядер метастабильных состояний впервые было дано в 1936 г. Вайцзеккером.

Статистический анализ распределения изомеров приводит к следующим закономерностям. Наибольшее число изомеров имеют ядра с нечетным массовым числом A. Изомеры достаточно часто встречаются у нечетно-нечетных ядер и очень редко у четно-четных. Это объясняется оболочечной моделью ядра, которая предсказывает существование в нечётных ядрах энергетически близких ядерных уровней с большим различием спинов (Δ J ≥4).[88] Последнему условию отвечают значения Z и N, лежащие непосредственно перед магическими числами 50, 82 и 126 (эти области Z и N часто называют островами изомерии).

^{180 m} Ta – возможно, единственный стабильный (в пределах чувствительности современных методик) изомер. Он существует в земной коре с момента её формирования и встречается в естественном тантале в соотношении 1: 8300. Хотя ^{180 m} Ta теоретически может распадаться, как минимум, тремя путями (изомерный переход, β^–-распад, электронный захват), ни один из них экспериментально не был обнаружен. Нижнее ограничение на период полураспада ^{180 m} Ta 1,2·10¹⁵ лет. В то же время основное состояние ¹⁸⁰Ta β-радиоактивно с Т _1/2 ≈ 8 ч. Спин и чётность основного состояния – 1⁺, изомера – 9⁻, причем изомерный уровень лежит выше основного всего на 75,3 кэВ. Таким образом, ввиду близости энергий и высокой разности спинов

состояний изомерный переход чрезвычайно сильно подавлен (как и превращения в соседние четно-четные изобары со спином и четностью 0⁺).

9.4. Внутренняя конверсия γ-квантов. Запаздывающие частицы. Другой способ снятия возбуждения ядра заключается в передаче им энергии одному из электронов атомных оболочек (К, L, M и т.д.). Диаграмма такого процесса изображена на рис. 9.2. Этот процесс, конкурирующий с изомерным переходом, называется простой внутренней конверсией γ-квантов, а испускаемые при этом электроны – конверсионными. В ряде случаев внутренняя конверсия является единственным процессом снятия возбуждения (например, в случае 0-0 переходов, когда испускание γ-квантов невозможно вообще).

Спектры конверсионных электронов дискретны, а их энергии T_i определяются соотношением

, (9.3)

где Δ Е – энергия данного изомерного перехода, ε_i – энергия связи электрона на i -ой оболочке атома. С наибольшей вероятностью внутренняя конверсия проходит на К -электронах. Однако, если энергия перехода меньше энергии связи К -электрона, конверсия на К -электронах становится энергетически невозможной и наблюдается конверсия на L -электронах, и т.д.

Отношение α среднего числа конверсионных электронов к среднему числу γ-квантов для конкретного перехода,

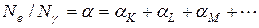, (9.4)

называется коэффициентом внутренней конверсии перехода. Для определения парциальных коэффициентов внутренней конверсии α_K, α_L, α_M и т.д. используют среднее число конверсионных электронов данной электронной оболочки.

Коэффициенты внутренней конверсии изменяются в широких пределах (10^–4–10³) и зависят от: а) энергии перехода (уменьшаются с ростом Δ Е); б) атомного номера ядра (растут с ростом Z и в первом приближении ~ Z ³); в) оболочки, которая принимает участие в конверсии (уменьшаются с ростом радиуса оболочки, т.е. α_K > α_L > α_M и т.д.); г) характера (электрического или магнитного) и мультипольности конкурирующего γ-излучения (растут с увеличением j). В результате тяжелые ядра с большей вероятностью испускают конверсионные электроны, чем легкие. Качественно все эти закономерности непосредственно вытекают из специфики изменения вероятности испускания γ-квантов, обсуждавшегося выше, а также строения электронных оболочек атома.

Расчёты коэффициентов внутренней конверсии проводятся методами квантовой теории поля с учётом экранирования заряда ядра электронами других оболочек атома и размеров ядра. Сравнение экспериментально измеренных коэффициентов внутренней конверсии с теоретическими значениями является одним из основных методов определения квантовых характеристик (спинов и чётностей) ядерных состояний.

Как и электронный захват, внутренняя конверсия γ-квантов, сопровождается характеристическим рентгеновским излучением, которое возникает в результате переходов электрона в состояние, освобожденное электроном конверсии. В результате конверсии могут появиться и электроны Оже. Различие между внутренней конверсией и испусканием электронов Оже состоит в том, что в первом случае энергия, уносимая электроном, передаётся ему от возбуждённого ядра, а во втором – от возбуждённой электронной оболочки атома.

Если энергия возбуждения ядра превышает удвоенную энергию покоя электрона 2 m_ec ² = 1,022 МэВ, может происходить процесс парной конверсии, при котором ядро теряет энергию возбуждения путем одновременного испускания электрона и позитрона (рис. 9.3). В этом случае спектры образующихся электронов и позитронов являются непрерывными, а суммарная кинетическая энергия электрон-позитронной пары равна разности энергии перехода и энергии, затраченной на ее рождение:

. (9.5)

Электронная оболочка атома не оказывает никакого влияния на парную конверсию и поэтому может происходить на ядре, лишенном всех атомных электронов. Однако вероятность парной конверсии обычно не превышает одной тысячной доли вероятности испускания γ -кванта.

Если энергия возбуждения превышает энергию отделения нуклона или группы нуклонов (чаще всего α-частицы), снятие возбуждения может произойти путем испускания их ядром. В этом случае частицы p, n, α и т.д. называют запаздывающими. Испускание запаздывающих протонов обычно наблюдается в цепочках β⁺-, а запаздывающих нейтронов – в цепочках β^–-распада.

9.5. Эффект Мёссбауэра. В 1958 г. было обнаружено явление резонансного поглощения γ -квантов, получившее название по имени автора открытия (немецкого физика Р. Мёссбауэра). Суть явления состоит в том, что если возбужденное ядро испускает γ -квант, то другое такое же невозбужденное ядро способно с большой долей вероятности его поглотить.

Для выяснения условий, при которых возможно резонансное поглощение, надо принять во внимание, что в процессе изомерного перехода энергия возбуждения Δ Е передается не только γ -кванту, но и самому ядру – в виде кинетической энергии ядра отдачи Т_я.о. Аналогично, при поглощении γ -кванта его энергия идет не только на возбуждение ядра, но и на сообщение ему дополнительного поступательного движения.

Воспользовавшись законом сохранения импульса и тем обстоятельством, что Т_я.о << Δ Е, нетрудно показать, что как при испускании, так и при поглощении γ -кванта

,

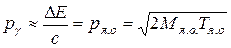откуда

. (9.6)

Таким образом, линии испускания и поглощения γ -квантов будут сдвинуты друг относительно друга на величину 2 Т_я.о. Иными словами, для резонансного поглощения ядрами требуются γ -кванты несколько большей энергии, чем та, что имеют испускаемые γ -кванты.

В силу квантовомеханического принципа неопределенности 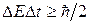источник излучения испускает (а поглотитель поглощает) не бесконечно тонкие спектральные линии, а линии конечной ширины , где τ – среднее время жизни возбужденного состояния. Величину Г называют естественной шириной спектральной линии, или просто шириной уровня. Для возможности резонансного поглощения γ -квантов необходимо, чтобы линии испускания и поглощения перекрывались (рис. 9.4), т.е. должно выполняться условие

. (9.7)

Рассмотрим на примере, выполняется ли данное условие для ядерного излучения. В качестве примера возьмем ядро ⁵⁷Fe. Энергия Δ Е возбуждения первого уровня этого ядра равна 14 кэВ, т.е. для γ -квантов это весьма малая величина. Среднее время жизни этого возбужденного состояния τ ≈ 10^–7 с, откуда естественная ширина линии Г ≈ 10^–8 эВ. Энергия отдачи при испускании γ -кванта с этого уровня, согласно (9.6), Т_я.о ≈ 10^–3 эВ, т.е превышает естественную ширину спектральной линии в 10⁵ раз. О выполнении условия (9.7) не может быть и речи![89] Поэтому резонансное поглощение γ -квантов изолированными ядрами невозможно.

Обратимся к испусканию и поглощению γ -квантов макроскопическими телами – кристаллами. Казалось бы, в и этом случае ситуация не изменится. Действительно, по законам классической механики при переходе от свободных ядер к связанным эффект отдачи несколько смягчится, но не настолько, чтобы сделать возможным резонанс. Однако в кристалле наряду с возбуждением колебаний индивидуальных ядер за счет энергии отдачи возможно возбуждение коллективных колебательных процессов, допускаемое квантовой механикой. Какой процесс произойдет – индивидуальный или коллективный – зависит от случая. Соотношение между числом тех и других процессов управляется законами квантовой статистики.

В коллективных процессах возбужденное ядро возвращается в основное состояние таким образом, что импульс отдачи воспринимается всем кристаллом в целом или, во всяком случае, большой группой атомов. Аналогично, энергия испущенного фотона поглощается отдельным ядром, а его импульс передается кристаллу как целому. Тогда на кинетическую энергию всего кристалла ввиду его большой массы приходится ничтожная доля. При таких переходах без отдачи, впервые обнаруженных и объясненных Мёссбауэром, и происходит резонансное поглощение γ -квантов. Условия для переходов без отдачи тем благоприятнее, чем ниже энергия изомерного перехода Δ Е и чем ниже (вопреки первоначальным ожиданиям самого Мессбауэра) температура кристалла.

Принципиальная схема наблюдения эффекта Мёссбауэра приведена на рис. 9.5-а. Источник γ -квантов Е медленно движется по окружности с помощью часового механизма относительно поглотителя А. За поглотителем расположен детектор γ -квантов D. Измеряется зависимость числа γ -квантов, попадающих на детектор в единицу времени, от скорости движения источника в моменты приближения и удаления его от поглотителя. Если линейная скорость v источника достаточно велика, то линия испускания сдвигается благодаря эффекту Доплера:

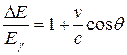. (9.8)

В этом случае резонансного поглощения нет. При уменьшении скорости доплеровский сдвиг уменьшается и линия испускания приближается к линии поглощения E_γ. Когда линии перекроются, начинается интенсивное резонансное поглощение. В результате интенсивность γ -излучения I, прошедшего через поглотитель, резко падает (рис. 9.5-б).

Основное применение эффекта Мёссбауэра связано с тем, что он дает уникальный метод измерения таких малых изменений энергии, которые не могут быть измерены никаким другим методом. Напрмиер, с его помощью удалось измерить гравитационное смещение спектральных линий, предсказанное общей теорией относительности Эйнштейна. Согласно этой теории, световой квант (фотон), распространяющийся вертикально в гравитационном поле Земли, при прохождении расстояния h меняет свою энергию Е_γ на такую величину Δ E, что

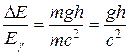, (9.9)

что проявляется в изменении его частоты. При падении фотона вниз частота увеличивается (фиолетовое смещение), а при поднятии вверх уменьшается (красное смещение). В 1959 г. Р. Паунд и Г. Ребка поставили соответствующий опыт в башне Гарвардского университета (h = 22,6 м), использовав в качестве излучателя и поглотителя образцы, содержащие ⁵⁷Fe, охлажденные до температуры жидкого гелия. Относительное изменение энергии фотона в этом случае, согласно (9.9), составляло около 2,5·10^–15, а абсолютное – около 3,4·10^–11 эВ, что примерно в 300 раз меньше естественной ширины линии. Следовательно, для надежного обнаружения эффекта необходимо измерять энергию с абсолютной погрешностью ~10^–12 эВ. Такая точность потребовала специальных условий проведения опыта и остроумных технических решений. Тем не менее, эффект был с уверенностью обнаружен, и полученный результат оказался в блестящем согласии с предсказанием Эйнштейна. В опыте Паунда и Ребки впервые в земных условиях было исследовано влияние гравитации на электромагнитные явления.

Высокое энергетическое разрешение при резонансном поглощении γ-квантов позволяет также наблюдать сверхтонкую структуру ядерных уровней, вызванную электронно-ядерными взаимодействиями. К последним относятся, в частности, взаимодействие магнитного момента ядра и электронов в магнитных материалах и взаимодействие квадрупольного момента ядра с градиентом электрического поля.[90] Для ряда возбужденных ядер, получивших название мёссбауэровских, таким путем стало возможно определить магнитный и электрический квадрупольный моменты. С другой стороны, эффект Мёссбауэра находит применение в физике твердого тела и материаловедении.

Дата добавления: 2015-05-26