Пример 2. Дан входной алфавит Q={0,1}, цепочка P из Q

Пример 1.

Дан входной алфавит Q={0,1}, цепочка P из Q.

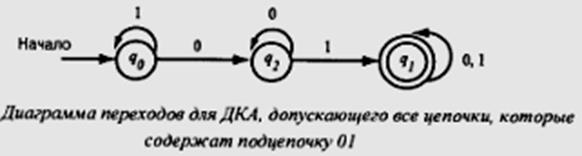
Построить автомат, допускающий все цепочки, содержащие подцепочку «01»

			F
q0	q2	q0
q1	q1	q1
q2	q2	q1

Построить автомат, который допускает язык L = {w|w}, содержащий четное число 0 и 1.

Решение.

Выделим 4 состояния, запоминающих четное и нечетное число 0 и 1:

Состояние q₀ одновременно допускающее и начальное, т. к. 0 – четное число.

Определение. Регулярный язык для некоторого автомата – это множество цепочек, приводящих автомат из начального состояния в одно из допускающих.

Например, для первого автомата язык - множество цепочек из 0 и 1, содержащих подцепочку 01, для второго автомата язык - множество цепочек из 0 и 1, содержащих четное число 0 и четное число 1.

Таким образом, язык: множество цепочек из 0 и 1, содержащих подцепочку «01» - можно задать распознающим автоматом А₀₁ = (Q,S,d,q₀,F), где Q={q₀,q₁,q₂}; S={0,1}; d - таблица или диаграмма переходов (см. выше); q₀ – начальное состояние; F={q₁} – множество заключительных состояний.

Язык L = {w|w}, содержащий четное число 0 и 1 можно задать распознающим автоматом А_L = (Q,S,d,q₀,F), где Q={q₀,q₁,q₂,q₃}; S={0,1}; d - диаграмма переходов (см. выше); q₀ – начальное состояние; F={q₀} – множество заключительных состояний.

Задать язык, содержащий подцепочку «000» распознающим конечным автоматом.

Автомат с магазинной памятью (АМП)

Как известно, распознавателем КС-языков является автомат с магазинной памятью.

Операции автомата:

1. «Вытолкнуть» – выталкивает из стека верхний символ (↑).

2. «Втолкнуть А» - вталкивает в стек магазинный символ А (↓ А).

3. «Заменить XYZ». Эквивалентна: ↑↓ X ↓ Y ↓ Z (↕ XYZ).

4. «Состояние t» - переход АМП в другое состояние ([t]).

5. «Сдвиг» («→») - сдвиг головки на один символ вправо относит. входной ленты.

Переход или шаг автомата – это выполнение операций над стеком и входной головкой, а также изменение состояния.

Автомат определяется:

1. Конечным множеством входных символов, включающим концевой маркер (┤).

2. Конечным множеством магазинных символов, включающим маркер дна (Ñ).

3. Конечным множеством состояний, включающим начальное состояние.

4. Программой устройства управления (УУ), которая каждой комбинации входного символа, магазинного символа и состояния ставит в соответствие выход или переход.

5. Начальным содержимым магазина, содержащим маркер дна и, возможно пустую, цепочку магазинных символов.

Автомат-распознаватель имеет 2 выходных сигнала: «Допустить» и «Отвергнуть».

При помощи МП-автоматов можно распознать б о льшую часть конструкций языков программирования. Рассмотрим некоторые из них.

Задача 1. Распознаватель скобочных выражений

Рассмотрим задачу проверки корректности вложенности круглых скобок.

Определим данный АМП:

1) Множество входных символов: { (, ), ┤ }.

2) Множество магазинных символов: { A, Ñ }

3) Множество состояний: t, является также и начальным состоянием автомата.

4) Алгоритм работы автомата.

- Если входная головка читает «(», то в магазин заталкивается символ А.

- Если входная головка читает «)», то из магазина выталкивается содержащийся там символ.

- Цепочка принимается, если при ее окончании всем левым скобкам нашлись правые, то есть при достижении символа ┤ магазин пуст Ñ.

- Цепочка отвергается, если:

1. Количество правых скобок превысило количество левых, т.е. на входе остаются правые скобки «)», а магазин пуст Ñ.

2. Входная цепочка прочитана до конца, а левым скобкам не нашлось пары, т.е. при достижении символа ┤ в магазине остаются символы А.

Магазинные символы	Входные символы
(	)	┤
А	↓A, →	↑, →	Отвергнуть
Ñ	↓A, →	Отвергнуть	Допустить

5) В начальном состоянии магазин содержит только маркер дна (Ñ).

Пример 1: (() ())

Номер шага	Содержимое стека	Остаток вх. цепочки
	Ñ	(() ()) ┤
	ÑA	() ()) ┤
	ÑAA	) ()) ┤
	ÑA	()) ┤
	ÑAA	)) ┤
	ÑA	) ┤
	Ñ	┤

Пример 2: ()))

Номер шага	Содержимое стека	Остаток вх. цепочки
	Ñ	())) ┤
	ÑA	))) ┤
	Ñ	)) ┤

Задача 2. Распознаватель арифметических выражений

Определим данный АМП:

1) Множество входных символов: { x, +, *, (, ), ┤ }.

2) Множество магазинных символов: { A, B, Ñ }

3) Множество состояний: t, является также и начальным состоянием автомата.

4) Алгоритм работы автомата.

- Цепочка принимается, если при ее окончании всем левым скобкам нашлись правые, для всех арифметическим знаков нашлись соответствующие «x».

- Цепочка отвергается, если:

1. Количество правых скобок превысило количество левых.

2. Количество «x» превысило количество арифметических знаков более чем на единицу.

3. Входная цепочка прочитана до конца, а левым скобкам не нашлось пары.

4. Входная цепочка прочитана до конца, а некоторым арифметическим знакам не нашлось соответствующих «x».

Алгоритм работы:

- Если входная головка читает «(», то в магазин заталкивается А.

- Если входная головка читает «)», то из магазина выталкивается А.

- Если входная головка читает «+» или «*», то в магазин заталкивается В.

- Если входная головка читает «х», то из магазина выталкивается В.

- Цепочка принимается, если при достижении символа ┤ магазин пуст Ñ.

- Цепочка отвергается, если:

1. На входе остаются правые скобки «)» или «х», а магазин пуст Ñ.

2. При достижении символа ┤ в магазине остаются символы А или В.

Магазинные символы	Входные символы
+, *	х	(	)	┤
А	↓В, →	Отвергнуть	↓A, →	↑, →	Отвергнуть
В	↓В, →	↑, →	↑↓A↓В, →	Отвергнуть	Отвергнуть
Ñ	↓В, →	Отвергнуть	↓A, →	Отвергнуть	Допустить

5) В начальном состоянии магазин содержит (ВÑ).

Пример 1: х+х*(х+х)

Номер шага	Содержимое стека	Остаток вх. цепочки
	ÑВ	х+х*(х+х) ┤
	Ñ	+х*(х+х) ┤
	ÑВ	х*(х+х) ┤
	Ñ	*(х+х) ┤
	ÑВ	(х+х) ┤
	ÑAB	х+х) ┤
	ÑA	+х) ┤
	ÑAB	х) ┤
	ÑA	) ┤
	Ñ	┤

Пример 2: x+x*(+x)

Номер шага	Содержимое стека	Остаток вх. цепочки
	ÑВ	х+х*(+х) ┤
	Ñ	+х*(+х) ┤
	ÑВ	х*(+х) ┤
	Ñ	*(+х) ┤
	ÑВ	(+х) ┤
	ÑAB	+х) ┤
	ÑABB	х) ┤
	ÑAB	) ┤

Теорема: класс языков, допускаемых МП-автоматами как по заключительному состоянию так и по пустому магазину совпадает с классом контекстно-свободных (КС) языков.

Задать язык списков типа а;[a;a;a;] распознающим АМП.

Определим данный АМП:

1) Множество входных символов: { a,;, [, ], ┤ }.

2) Множество магазинных символов: { A, B, Ñ }

3) Множество состояний: t, является также и начальным состоянием автомата.

4) Алгоритм работы автомата.

- Цепочка принимается, если при ее окончании всем левым скобкам нашлись правые, для всех «a» нашлись соответствующие «;».

- Цепочка отвергается, если:

1. Количество правых скобок превысило количество левых.

2. Количество «;» превысило количество «a».

3. Входная цепочка прочитана до конца, а левым скобкам не нашлось пары.

4. Входная цепочка прочитана до конца, а для некоторых элементов «a» не нашлось символа конца «;».

Алгоритм работы:

- Если входная головка читает «(», то в магазин заталкивается А.

- Если входная головка читает «)», то из магазина выталкивается А.

- Если входная головка читает «а», то в магазин заталкивается В.

- Если входная головка читает «;», то из магазина выталкивается В.

- Цепочка принимается, если при достижении символа ┤ магазин пуст Ñ.

- Цепочка отвергается, если:

1. На входе остаются правые скобки «)» или «;», а магазин пуст Ñ.

2. При достижении символа ┤ в магазине остаются символы А или В.

5) В начальном состоянии магазин пуст (Ñ).

Магазинные символы	Входные символы
a	;	(	)	┤
А	↓В, →	Отвергнуть	↓A, →	↑, →	Отвергнуть
В	↓В, →	↑, →	Отвергнуть	Отвергнуть	Отвергнуть
Ñ	↓В, →	Отвергнуть	↓A, →	Отвергнуть	Допустить

Пример 1: a;a;(a;a;)

Номер шага	Содержимое стека	Остаток вх. цепочки
	Ñ	a;a;(a;a;) ┤
	ÑВ	;a;(a;a;) ┤
	Ñ	a;(a;a;) ┤
	ÑВ	;(a;a;) ┤
	Ñ	(a;a;) ┤
	ÑA	a;a;) ┤
	ÑAB	;a;) ┤
	ÑA	a;) ┤
	ÑAB	;) ┤
	ÑA	) ┤
	Ñ	┤

Пример 2: a;a;(;a;)

Номер шага	Содержимое стека	Остаток вх. цепочки
	Ñ	a;a;(;a;) ┤
	ÑВ	;a;(;a;) ┤
	Ñ	a;(;a;) ┤
	ÑВ	;(;a;) ┤
	Ñ	(;a;) ┤
	ÑA	;a;) ┤

Дата добавления: 2015-05-26