Объединение 3-х и более алгоритмов

Задача. Автомат должен выполнять три алгоритма U ₁, U ₂ и U ₃ в зависимости от значений набора логических условий r₁, r₂.

Получить минимизированный объединенный алгоритм U _об, в котором отсутствуют повторяющиеся операторы.

Алгоритм решения.

1. Составить граф-схему и логическую схему каждого алгоритма.

2. Оценить эффективность минимизации объединенного алгоритма по количеству общих (одинаковых) операторов и логических переменных исходных алгоритмов. Если это количество меньше 2, то минимизация неэффективна, U _об = r₁­¹r₂­² U ₁w­³ ¯¹ U ₂w­³¯² U ₃¯³, иначе перейти к п. 3.

3. Составить матричную схему каждого алгоритма.

4. Построить объединенную МСА, каждый элемент которой

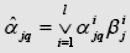
где

Определяющие функции вычисляются по формуле:

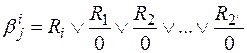
Здесь R_i - определяющие конъюнкции для всех объединяемых МСА.

Оператор А_i входит только в ЛСА U _i, поэтому есть выбор R/0, который позволяет минимизировать систему формул перехода и объединенную ЛСА.

Практика объединения алгоритмов показывает, что МСА с наибольшим числом совпадающих элементов желательно приписывать определяющие конъюнкции с соседним кодированием.

Совпадающие элементы:

- элементы, состоящие из одинаковых логических функций;

- элементы строки оператора А_i, если он отсутствует в другой МСА.

4.1. Построить неориентированный граф, вершины которого помечены обозначениями алгоритмов, а ребра - числом совпадающих элементов.

4.2. Закодировать определяющие конъюнкции алгоритмов набором логических переменных r₁r₂, используя соседнее кодирование для пар МСА с наибольшим числом совпадающих элементов.

4.3. Построить набор определяющих функций для каждого оператора каждого алгоритма.

4.4. Построить объединенную МСА.

5. Составить систему формул перехода, провести ее минимизацию и упрощение.

6. По системе схемных формул перехода составить объединенную ЛСА.

7. Проверить выполнение каждого алгоритма в объединенной ЛСА, подставляя соответствующие значения r₁, r₂. Если алгоритм имеет большое количество элементарных выражений и безусловных переходов, то проверку рекомендуется проводить по объединенной ГСА.

Пример. U ₁ – вывести максимум массива из 10 элементов.

U ₂ – вывести минимум массива из 10 элементов.

U ₃ – вывести номер первого элемента массива, равного 4.

1)

U ₁ =A₀A₁₁¯²p₁₁­¹¹A₂₁¯¹¹A₃p₂­²A₄₁A_к

U ₂ =A₀A₁₂¯²p₁₂­¹²A₂₂¯¹²A₃p₂­²A₄₂A_к

U ₃ =A₀A₁₃¯²p₁₃­¹³A₂₃ω­³¯¹³A₃p₂­²¯³A_к

2) Общие операторы и логические переменные – A₀ , A₃ , p₂ , A_к . Минимизация должна быть эффективна.

3)

U ₁

	A11	A21	A3	A41	Aк
A0
A11		p11	!p11
A21
A3		!p2p11	!p2!p11	p2
A41					1

U ₂

	A12	A22	A3	A42	Aк
A0
A12		p12	!p12
A22
A3		!p2p12	!p2!p12	p2
A42					1

U ₃

	A13	A23	A3	Aк
A0
A13		p13	!p13
A23
A3		!p2p13	!p2!p13	p2

4) Определяющие конъюнкции и функции

4.1) Граф с числами совпадающих элементов

U ₁- U ₂: строки А₁₁+А₂₁+А₁₂+А₂₂+А₄₁+А₄₂ = 2+1+2+1+1+1 = 8.

U ₁- U ₃: строки А₁₁+А₂₁+А₄₁+А₁₃+А₂₃ = 2+1+1+2+1 = 7.

U ₂- U ₃: строки А₁₂+А₂₂+А₄₂+А₁₃+А₂₃ = 2+1+1+2+1 = 7.

Для большей минимизации введена пустая МСА U _ø , число совпадающих с ней элементов равно числу элементов всей матрицы.

4.2) Определяющие конъюнкции

Наибольшее число совпадающих элементов у пар матриц U ₁- U ₂ , U ₁- U _ø , U ₂- U _ø .

Закодируем определяющие конъюнкции для U ₁ , U ₂ , U _ø соседними кодами:

R₁ = r₁r₂, R₂ = r₁!r₂, R _ø =!r₁r₂, R₃ =!r₁!r₂.

4.3) Определяющие функции

Определяющие функции операторов А₀ и А₃ первого алгоритма (присутствуют во всех алгоритмах кроме пустого):

.

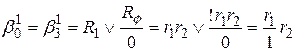Определяющие функции остальных операторов первого алгоритма (присутствуют только в нем):

.

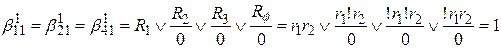Аналогично для остальных алгоритмов:

;

;

.

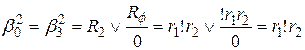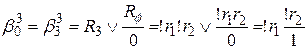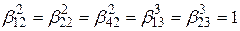4.4) Объединенная недоопределенная МСА

	A11	A12	A13	A21	A22	A23	A3	A41	A42	Aк
A0	(r1/1)r2	r1!r2	!r1(!r2/1)
A11				p11			!p11
A12					p12		!p12
A13						p13	!p13
A21
A22
A23
A3				!p2p11 (r1/1)r2	!p2p12r1!r2	!p2p13!r1(!r2/1)	!p2!p11(r1/1)r2v !p2!p12r1!r2 v !p2!p13!r1(!r2/1)	p2(r1/1)r2	p2r1!r2	p2!r1 (!r2/1)
A41
A42

Доопределяем МСА, сокращая число и сохраняя полноту логических условий.

	A11	A12	A13	A21	A22	A23	A3	A41	A42	Aк
A0	r1r2	r1!r2	!r1
A11				p11			!p11
A12					p12		!p12
A13						p13	!p13
A21
A22
A23
A3				!p2p11 r1r2	!p2p12r1!r2	!p2p13!r1	!p2!p11r1r2v !p2!p12r1!r2 v !p2!p13!r1	p2r1r2	p2r1!r2	p2!r1
A41
A42

5) Скобочная система формул перехода S₂

A₀ → r₁r₂A₁₁ V r₁!r₂A₁₂ V!r₁A₁₃ → r₁(r₂A₁₁ V!r₂A₁₂) V!r₁A₁₃

A₁₁ → p₁₁A₂₁ V!p₁₁A₃

A₁₂ → p₁₂A₂₂ V!p₁₂A₃

A₁₃ → p₁₃A₂₃ V!p₁₃A₃

A₂₁ → A₃

A₂₂ → A₃

A₂₃ → A_к

A₃ →!p₂r₁r₂(p₁₁A₂₁ V!p₁₁A₃) V!p₂r₁!r₂(p₁₂A₂₂ V!p₁₂A₃) V!p₂!r₁(p₁₃A₂₃ V!p₁₃A₃) V p₂(r₁(r₂A₄₁ V!r₂A₄₂) V!r₁A_к) → p₂(r₁(r₂A₄₁ V!r₂A₄₂) V!r₁A_к) V!p₂(r₁(r₂(p₁₁A₂₁ V!p₁₁A₃) V!r₂(p₁₂A₂₂ V!p₁₂A₃)) V!r₁(p₁₃A₂₃ V!p₁₃A₃))

A₄₁ → A_к

A₄₂ → A_к

Схемная система формул перехода S₃

A₀ → r₁­¹r₂­²A₁₁ * ¯²A₁₂ * ¯¹A₁₃

A₁₁ → p₁₁­¹¹A₂₁ * ¯¹¹A₃

A₁₂ → p₁₂­¹²A₂₂ * ¯¹²A₃

A₁₃ → p₁₃­¹³A₂₃ * ¯¹³A₃

A₂₁ → A₃

A₂₂ → A₃

A₂₃ → A_к

A₃ → p₂­³ r₁­⁴ r₂­⁵A₄₁ * ¯⁵A₄₂ * ¯⁴A_к * ¯³ r₁­⁶ r₂­⁷ p₁₁­¹¹A₂₁ * ¯¹¹A₃ * ¯⁷ p₁₂­¹²A₂₂ * ¯¹²A₃ * ¯⁶ p₁₃­¹³A₂₃ * ¯¹³A₃

A₄₁ → A_к

A₄₂ → A_к

Преобразованная схемная система формул перехода S₃'

A₀ → r₁­¹ r₂­² A₁₁ * ¯²A₁₂ * ¯¹A₁₃

A₁₁ → ¯³ r₁­⁶ r₂­⁷ p₁₁­⁸A₂₁

A₁₂ → ¯⁷ p₁₂­⁸A₂₂

A₁₃ → ¯⁶ p₁₃­⁸A₂₃

A₂₁ → ω­⁸

A₂₂ → ¯⁸A₃

A₂₃ → ω­⁹

A₃ → p₂­³ r₁­⁹ r₂­⁵A₄₁ * ¯⁵A₄₂

A₄₁ → ω­⁹

A₄₂ → ¯⁹A_к

6) Объединенная ЛСА

U _об = A₀ r₁­¹ r₂­²A₁₁¯³ r₁­⁶ r₂­⁷ p₁₁­⁸A₂₁ω­⁸¯²A₁₂¯⁷ p₁₂­⁸A₂₂¯⁸A₃ω­¹⁰¯¹A₁₃¯⁶ p₁₃ ­⁸A₂₃ω­⁹ ¯¹⁰ p₂­³ r₁­⁹ r₂­⁵A₄₁ω­⁹¯⁵A₄₂¯⁹A_к

7) Проверка:

r₁=1, r₂=1 U₁ = A₀A₁₁¯³p₁₁­⁸A₂₁¯⁸A₃p₂­³A₄₁A_к

r₁=1, r₂=0 U₂ = A₀A₁₂¯³p₁₂­⁸A₂₂¯⁸A₃p₂­³A₄₂A_к

r₁=0, r₂=0 U₃ = A₀A₁₃¯³p₁₃­⁸A₂₃ω­⁹¯⁸A₃p₂­³¯⁹A_к

При подстановке соответствующих значений r все 3 алгоритма выполняются правильно, следовательно объединенная ЛСА составлена верно.

В объединенной ЛСА 21 элементарное выражение, а в необъединенной – 25. Минимизация эффективна.

Задача для подготовки.

Объединить 3 алгоритма:

U ₁ – вывести максимум массива из 10 элементов.

U ₂ – вывести номер первого элемента массива, большего 5.

U ₃ – упорядочить массив в порядке возрастания и вывести последний элемент.

Первый оператор А₀ – инициализация массива и переменных.

Последний оператор А_к – вывод искомого значения на экран.

Дата добавления: 2015-05-26