Лекция 10. Электронные состояния и электронно-колебательно-вращательные спектры молекул (УФ)

Электронные состояния и электронно-колебательно-вращательные спектры молекул (УФ). Спектры двухатомных молекул. Классификация электронных состояний и разрешенные переходы. Колебательная структура. Таблица и серии Деландра. Принцип Франка-Кондона. Определение энергии диссоциации. Вращательная структура.

Классификация электронных состояний двухатомных молекул по проекции орбитального момента количества движения.

Эта классификация основана на следующем.

Орбитальный момент. Квадрат суммарного вектора L момента количества движения всех электронов молекулы определяется выражением:

L² =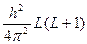

где L – соответствующее квантовое число.

Каждое электронное состояние двухатомной молекулы характеризуется определенным значением проекции орбитального момента количества движения на линию, соединяющую ядра молекулы. Эта проекция выражается в виде:

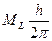
где 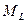- квантовое число проекции орбитального момента – может быть равно одному из чисел:

Состояния, отличающиеся только знаком 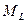, не различаются по энергии. Различия в энергии определяются числом 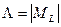. Ряд других свойств состояний также определяются числом 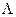, поэтому электронные состояния классифицируют по значению этого числа:

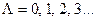
соответствуют символам

Магнитное поле, связанное с орбитальным моментов электронов, определяется проекцией орбитального момента на межъядерную ось, т.е. определяется квантовым числом 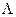и направлено вдоль межъядерной оси.

Для 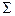-состояний напряженность магнитного поля равна 0, для других – пропорциональна числу .

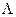Спин, компонеты мультиплета. Квадрат вектора суммарного спина всех электронов 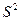определяется квантовым числом суммарного спина.

S² =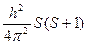

Квантовое число может быть целым (при четном количестве электронов) и полуцелым (при нечетном количестве электронов). Проекция суммарного вектора на межъядерную ось будет

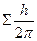
где 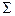- квантовое число проекции суммарного спина – может быть равно одному из чисел: 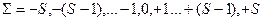(не путать с 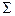, определяющим квантовое состояние ).

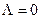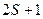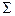Совокупность состояний, имеющих одно и тоже значение и разные значения , называется мультиплетом, а отдельные состояния – компонентами мультиплета. Энергия компонента мультиплета определяется напряженностью внутреннего магнитного поля молекулы, пропорциональной 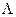, и проекцией 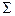суммарного вектора спина на межъядерную ось. Если обозначить среднюю энергию мультиплета через 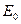, то энергии отдельных его компонент может быть выражена:

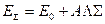
Например, для состояния ():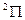

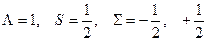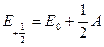
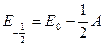
Каждый компонент мультиплета может быть охарактеризован суммарной проекцией орбитального и спинового моментов на межъядерную ось. Квантовое число этой проекции равно . Отдельные компоненты мультиплета обозначаются символом состояния и значением 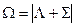, которое ставится как нижний индекс справа. В примере

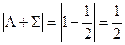
И компоненты дублета будут обозначаться как и .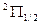

Дата добавления: 2015-05-26