Алгоритм навчання Хебба

У 1949г. канадський психолог Д.Хебб опублікував книгу “Організація поведінки” (D.Hebb “Organizational Behaviour”), в якій він постулював правдоподібний механізм навчання на клітинному рівні в мозку.Основна ідея Хебба полягала у тому, що коли вхідний сигнал нейрона, що поступає через синаптитчні зв'язки, викликає спрацьовування нейрона, то ефективність такого входу в термінах його здатності сприяти спрацьовуванню нейрона в майбутньому повинна збільшуватися. Хебб припустив, що зміна ефективності повинна відбуватися саме в синапсі, який подає цей сигнал на вхід нейрона призначення. Пізніші дослідження підтвердили цю здогадку Хебба. Хоча останнім часом були відкриті інші механізми біологічного навчання на клітинному рівні, у визнання заслуг Хебба піонерського характеру цей закон навчання був названий в його честь.Закон навчання Хебба належить до класу законів навчання по змаганню [19].

Метод навчання Хебба полягає у зміні ваг за наступним правилом:

	(2.4.)

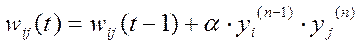
Де y_i(n-1) - вихідне значення нейрона i шару (n-1), y_j(n) - вихідне значення нейрона j шару n; w_ij(t) і w_ij(t-1) - ваговий коефіцієнт синапсу, що з'єднує ці нейрони, на ітераціях t і t-1 - коефіцієнт швидкості навчання a відповідно; Тут і далі, для спільності, під n мається на увазі довільний шар мережі. При навчанні за цим методом посилюються зв'язки між збудженими нейронами.

Існує також і диференційний метод навчання Хебба.

	(2.5.)

Тут y_i^(n-1)(t) і y_i^(n-1)(t-1) - вихідне значення нейрона i шару n-1 відповідно на итерация t і t-1; y_j⁽ⁿ⁾(t) і y_j⁽ⁿ⁾(t-1) - те ж саме для нейрона j шару n. Як видно з формули (2), найсильніше навчаються синапси, що з'єднують нейрони ті, виходи яких найбільш динамічно змінилися у бік збільшення.

На мал. 2.4. представлена архітектура нейронної мережі, що складається з нейронів, які називаються “лінійними асоціаторами”.

Рис. 2.4. Нейронна мережа з m елементів [19].

Повний алгоритм навчання із застосуванням вищенаведених формул буде виглядати так:

1. На стадії ініціалізації всім ваговим коефіцієнтам присвоюються невеликі випадкові значення.

2. На входи мережі подається вхідний образ, і сигнали збудження поширюються по всіх верствах згідно з принципами класичних прямопоточних (feedforward) мереж, тобто для кожного нейрона розраховується зважена сума його входів, до якої потім застосовується активаційна функція нейрона, в результаті чого виходить його вихідне значення yi(n), i = 0... Mi-1, де Mi - кількість нейронів у шарі i; n = 0... N-1, а N - число шарів у мережі.

3. На підставі отриманих вихідних значень нейронів за формулою (2.4.) або (2.5.) проводиться зміна вагових коефіцієнтів.

4. Цикл із кроку 2, поки вихідні значення мережі не стануть стабільними із заданою точністю. Застосування цього нового способу визначення завершення навчання, відмінного від використався для мережі зворотного поширення, обумовлено тим, що підлаштовувалася значення синапсів фактично не обмежені (додаток А).

Хід виконання

Завдання 1. Задання початкових значень вагових коефіцієнтів для вхідного і вихідного прошарків.

Візуальний інтерфейс програми

В даній програмі ми будемо працювати з такими компонентами:

TButton (закладка Standard) використовується для створення кнопок;

TLabel (закладка Standard) використовується для створення напису (мітки)

TSpinEdit (закладка Samples) використовується для створення текстового поля з стрілками;

TSpeedButton (закладка Additional) використовується для формування пенелей управління;

TStringGrid (закладка Additional) використовується для створення таблиць.

1. Для початку в розділі type прописуємо такі змінні:

v= array of real;

m = array of v;

і в розділі змінних задаємо такі значення

w:m;

2. Використовуємо компоненту StringGrid.

3. Використовуємо 3 кнопочки SpinEdit і біля кожної з цих кнопочок створюємо компонент Label з такими назвами:

«Вхідний шар» біля компоненти SpinEdit1;

«Вихідний шар» біля компоненти SpinEdit2;

«Кількість вхідних масивів» біля компоненти SpinEdit3.

4. Використовуємо компоненту SpeedButton. Прописуємо текст програми для цієї кнопочки:

var i,j:integer;

begin

StringGrid1.ColCount:=StrToInt(Edit1.Text)+1;

StringGrid1.RowCount:= StrToInt(Edit2.Text)+1;

for i:=1 to StringGrid1.ColCount do

StringGrid1.cells[i,0]:='In'+IntToStr(i);

for j:=1 to StringGrid1.ColCount do

StringGrid1.Cells[0,j]:='Out'+ IntToStr(j);

SetLength(w, StrToInt(Edit3.text));

for i:=0 to StrToInt(Edit3.Text)-1 do

SetLength(w[i], StrToInt(Edit1.Text));

end;

Використовуємо компоненту Button, називаємо її «початкові значення». Прописуємо текст для цієї кнопочки:

var i,j:integer;

begin Randomize;

Button2.Enabled:=False;

for i:=0 to StrToInt(Edit1.Text)-1 do

for j:=0 to StrToInt(Edit2.Text)-1 do

StringGrid1.Cells[i+1,j+1]:=IntToStr(i);

Використовуємо ще одну компоненту Button, в якій прописуємо вихід з програми.

Завдання 2. Задати початковий розподіл з використанням синаптичних ваг з розподілом псевдо автоматичної функції.

Завдання 3. Навчання та тестування нейронної мережі.

Дата добавления: 2015-05-26