Многоуровневый эксперимент как контрольный

Сначала мы рассмотрим, что дает многоуровневый эксперимент, когда экспериментальная гипотеза может быть проверена и с использованием только двух условий. Примером может служить эксперимент по рабочей этике, обсуждавшийся в главе 5, где было показано, что девочки-индианки предпочитают активные усилия безделью. Сравнивались два условия: (1) получение шарика без нажатия на рычаг и (2) получение шарика после 10-кратного нажатия на рычаг. Можно было бы использовать различное число нажатий, например 2, 5, 10, 50 за каждый шарик. Улучшился ли бы эксперимент при введении большого числа уровней настолько, чтобы его стоило проводить? (Хотя, учитывая гипотезу авторов, ответ заранее ясен: многоуровневый эксперимент должен бы предпочитаться исследователями, поскольку он требует больше активных усилий с их стороны.)

Меньше шансов пропустить эффект

Чтобы увидеть преимущество пятиуровневого эксперимента, следует ответить на вопрос, каким образом экспериментаторы узнали, что для одного из двух экспериментальных условий необходимо использовать именно десять нажатий на рычаг. Возможно, — это слишком небольшая работа, чтобы влиять на поведение, а может быть, наоборот, слишком большая. Очевидно, исследователи Сингх и Квери (1971) просто решили, что одного нажатия на шарик будет слишком мало. Точно так же нельзя предлагать очень много нажатий за одни шарик, ибо в этой случае девочки будут, безусловно, стремиться получать шарики просто так, и лишь где-то между этими крайними значениями будет находиться число нажатий (уровень), при котором активное и пассивное условия окажутся одинаково предпочитаемыми. Если бы Сингх и Квери остановили свой выбор на уровне равного предпочтения, они оказались бы в том же положении, что и воображаемый экспериментатор В, чьи результаты показывают, что независимая переменная не оказывает никакого действия. Проделанный сейчас анализ показывает, что гипотеза, проверявшаяся в исследовании Сингха и Квери, в действительности была количественной гипотезой, соотносящей количество нажатий на рычаг с величиной предпочтения активных усилий пассивной награде. Хорошо проверить такую гипотезу можно только при условии, если независимая переменная будет непрерывна. Это, конечно, невозможно, поскольку тогда потребуется бесконечное число уровней с бесконечно малыми различиями. И все же при использовании даже пяти уровней можно приблизиться к выявлению полного отношения между независимой и зависимой переменными. По мере уменьшения числа уровней увеличивается опасность ошибочного представления этого отношения. Поэтому можно сказать, что внутренняя валидность больше, когда такая гипотеза проверяется при пяти уровнях по сравнению с двумя уровнями независимой переменной. Эта угроза внутренней валидности вытекает из неполноты независимой переменной. Угрозы, описанные выше, проистекали либо из ненадежности 9данных, либо из процедурного или сопутствующего смешения с другими переменными (см. гл. 5, с. 193). Воображаемые эксперименты А, Б и В служат драматическим примером того, как ложно может быть представлено отношение между независимой и зависимой переменными из-за использования небольшого числа уровней. Кроме того, эксперимент с двумя уровнями сталкивается еще с одной проблемой, касающейся сопутствующего смешения. К показу этого мы сейчас и перейдем.

Лучший контроль над сопутствующим смешением

Доказательство действия независимой переменной неубедительно, если явно возможно сопутствующее смешение, т. е. если активный уровень независимой переменной связан с активным уровнем другой переменной. Контрольные же условия, подобные описанным в главе 5, могут оказаться менее эффективными, чем это кажется.

Предположим, что на студентах колледжа проводится эксперимент для выяснения того, усиливает ли кофеин реактивность нервной системы по отношению к стимуляции. Измеряемым параметром служит время реакции. Если бы использовалось только два условия, существовала бы ясная опасность обсуждаемого смешения. Пусть, например, в качестве активного уровня выбрано 3 миллиграмма лекарства на каждый килограмм веса испытуемого. (На основании других исследований можно судить, что этот выбор удачный.) Как обсуждалось в главе 5, контрольным условием должно быть нейтральное вещество - плацебо. Если кофеин дается в виде таблетки, плацебо тоже должно быть таблеткой, но не содержащей активного вещества. И все же плацебо может не обеспечить контроль за осведомленностью испытуемого относительно предъявляемого условия. Здесь не учитывается тот факт, что испытуемый (особенно хороший студент колледжа) может определить, является ли таблетка кофеином или нейтральным веществом. В первом случае появится слабое дрожание пальцев, учащенное дыхание, разольется тепло но лицу и т. д. Осознание этого вполне может оказать косвенное влияние на время реакции. Испытуемый может ожидать, что его ответы станут более живыми, напряжение его повысится, что действительно приведет к сокращению времени реакции. Такое действие кофеина не будет иметь ничего общего с гипотезой экспериментатора о непосредственном действии кофеина на нервную систему. Здесь произойдет сопутствующее смешение. Активный уровень независимой переменной (3 мг кофеина на 1 кг веса) окажется неразрывно связанным с активным уровнем другой переменной – осознанием факта его приема.

Если же вместо двухуровневого эксперимента провести многоуровневый эксперимент с дозами 0, 1, 2, 3, 4 и 5 миллиграммов кофеина на килограмм веса, можно получить кривую, показанную на рис. 7.2. Уровень нулевой дозировки, конечно, обозначает плацебо. На рисунке видно постепенное сокращение времени реакции по мере продвижения от дозы 1 к дозе 5. Более резкое падение кривой от 0 к 1 может быть частично следствием осознания факта приема кофеина. Однако дальнейшее регулярное изменение дает достаточно убедительное доказательство того, что кофеин непосредственно увеличивает реактивность. Мало вероятно, что эта кривая может быть результатом нарастающего осознания увеличивающихся доз вещества. Если экспериментатора специально интересует действие плацебо, он может организовать еще одно контрольное условие: вовсе не давать никакой таблетки. Это условие представлено на рис. 7.2 треугольником. Меньшее время реакции при нулевой дозе кофеина (плацебо) показывает, что в самом деле имеет место действие плацебо, равно как и осознания принятия кофеина, равно как и непосредственное действие кофеина. Как много может происходить в простом эксперименте!

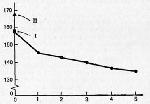
Рис. 7.2. Результаты воображаемого многоуровневого эксперимента с влиянием кофеина на время реакции. Ось абсцисс — дозы кофеина (мг/кг). Ось ординат — время реакции (мс). I — плацебо, II — без таблетки

В двухуровневых экспериментах вероятность такого сопутствующего смешения очень велика. В эксперименте по трудовой этике, когда девочка нажимала на рычаг, она, наверное, делала нечто большее, чем зарабатывала 1 шарик за 10 нажатий. Таким способом она осуществляла также контакт с невидимым ей экспериментатором (или с тем, что, по ее (предположению, находилось в большом ящике). Поэтому в какой-то степени нажатие рычага могло оказаться связанным с активным уровнем второй переменной — установлением контакта с невидимым экспериментатором. В многоуровневом эксперименте с использованием различного числа необходимых нажатий на рычаг постепенное увеличение предпочтения по мере увеличения числа нажатий было бы более четким доказательством экспериментальной гипотезы. Однако если бы небольшое количество работы (например 1 шарик за каждое нажатие) выбиралось также охотно, как и большее количество работы (например 1 шарик за каждые пять нажатий), доказательство гипотезы было бы слабым. И снова многоуровневый эксперимент исключил бы опасность сопутствующего смешения.

Дата добавления: 2015-05-26