Основные термины и положения термодинамики

Термодинамические системы

В термодинамике изучаются физические системы, состоящие из большого числа частиц и находящиеся в состоянии термодинамического равновесия или близком к нему. Такие системы называются термодинамическими системами. Это понятие в общем случае достаточно сложно определить строго, поэтому используется описательное определение, в котором термодинамической системой называется макроскопическая система, которая каким-то образом (например, с помощью реальной или воображаемой оболочки) выделена из окружающей среды и способна взаимодействовать с ней. Если оболочка не допускает обмен ни веществом, ни энергией между системой и окружающей средой, то такая оболочка называется адиабатической, а соответствующая система - изолированной или замкнутой. Системы, у которых оболочка не препятствует обмену веществом и энергией, называются открытыми.

Система – это совокупность материальных объектов (тел), ограниченных каким-либо образом от окружающей среды.

В зависимости от характера взаимодействия с окружающей средой термодинамические системы делятся на три типа:

1) изолированная – система, которая не обменивается с окружающей средой ни веществом, ни энергией;

2) замкнутая – система, которая может обмениваться с окружающей

средой лишь энергией и не может обмениваться веществом;

3) открытая – система, которая обменивается с окружающей средой и

энергией, и веществом.

Живые организмы являются открытыми системами.

Состояние любой термодинамической системы характеризуется двумя группами параметров:

Интенсивными термодинамическими параметрами (давление, температура и др.), не зависящими от массы или числа частиц в системе;

Экстенсивными термодинамическими параметрами (общая энергия, энтропия, внутренняя энергия), зависящими от массы или числа частиц в системе.

Изменение параметров термодинамической системы называется термодинамическим процессом.

Энергию системы (W) можно представить как совокупность двух частей: зависящую от движения и положения системы как целого (W _ц) и не зависящую от этих факторов (U).

W = W ц+ U

(1.1)

Вторую составляющую этой совокупности U называют внутренней энергией системы.

Она включает энергию теплового движения частиц, а также химическую и ядерную энергию, определяющую поступательное, колебательное и вращательное движение молекул, внутримолекулярное взаимодействие и колебание атомов, энергию вращения электронов.

Внутренняя энергия в свою очередь разделяется на свободную энергию и связанную энергию.

Свободная энергия (G) – та часть внутренней энергии, которая может быть использована для совершения работы.

Связанная энергия (W _св) – та часть энергии, которую нельзя превратить в работу.

U = G + W св

(1.2)

Вопрос 47 сама5.1. Первый закон термодинамики для потока На практике при рассмотрении рабочих процессов машин, аппаратов и устройств, встречаются задачи изучении закономерностей движения рабочих тел (газов, пара и жидкостей). Уравнение 1-го закона термодинамики для потока газа при следующих допущениях: движение газа по каналу установившееся и неразрывное; скорости по сечению, перпендикулярному оси канала, постоянны; пренебрегается трение частичек газа друг другу и о стенки канала; изменение параметров по сечению канала мало по сравнению их абсолютными значениями, имеет вид: q = Du + De + lпрот. + lтехн., (5.1) где De = (w22 – w21)/2 + g·(z2 –z1) – изменение энергии системы, состоящий из изменения кинетической и потенциальной энергий; w1,w2 – скорости потока в начале и в конце канала; z1, z2 – высота положения начала и конца канала. lпрот. = P2·n 2 – P1·n 1– работа проталкивания, затрачиваемая на движения потока; lтехн. – техническая (полезная) работа (турбины, компрессора, насоса, вентилятора и т.д.). q = (u2 – u1) + (w22 – w21)/2 + g·(z2 –z1) + P2·n 2 – P1·n 1 + lтехн. (5.2) Введем понятия энтальпии, который обозначим через величину: h = u + Pх, (5.3) h2 = u2 + P2·n 2; h1 = u1 + P1·n 1. (5.4) Тогда уравнение 1-го закона термодинамики для потока газа будет иметь вид: q = h2 – h1 + (w22 – w21)/2 + g·(z2 –z1) + lтехн. (5.5)

Вопрос 48

Истечение паров, жидкостей и газов.

Процесс истечения – процесс переноса вещества из области с одним давлением в область с другим.

Действительный процесс истечения характеризуется необратимыми потерями и неравномерностью распределения скоростей в потоке. В теории истечение рассматривается, как обратимый процесс, а переход к реальным характеристикам осуществляется с помощью двух коэффициентов: коэффициента скорости - и коэффициента расхода - 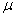, причём эти коэффициенты определяются экспериментальным путём. Оба коэффициента показывают различия между теоретическими и действительными величинами.

Нас интересуют следующие величины:

1. Линейная скорость - , .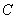

2. Массовая скорость - , .

3. Массовый расход - , .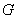

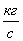Задача решается на базе следующих уравнений:

1. Первое начало термодинамики: .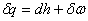

2. Уравнение процесса:

a. Политропный процесс: .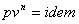

b. Адиабатный процесс: .

3. Уравнение неразрывности в интегральном виде: .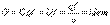

4. Уравнение состояние.

Основные соотношения процесса истечения.

Уравнение распределения потенциальной работы:

.

Так как рассматриваются обратимые потери, то .

Так как рассматривается чистое движение, то .

Следовательно: .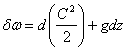

Так как рассматриваются короткие каналы, то , .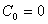

Выражение для линейной скорости: .

Выражение для массовой скорости: .

Выражение для массового расхода: .

Основные исходные соотношения.

Уравнение для линейной скорости: .

Уравнение для массовой скорости: .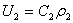

Уравнение для массового расхода: .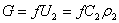

Истечение сжимаемых жидкостей (паров и газов).

Условия сжимаемости жидкости: , .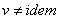

Рассматриваем политропный процесс истечения: 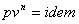. В случае, если , то получаем адиабатный процесс истечения.

Потенциальную работу можно найти по следующей формуле: , где . Тогда 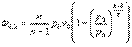. Подставив полученное выражение в уравнение для линейной скорости, получим: - уравнение линейной скорости для политропного процесса.

Уравнение линейной скорости для адиабатного процесса 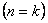будет иметь следующий вид: .

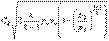В уравнение для массовой скорости 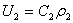входит плотность , которая меняется в течение процесса. Из уравнения политропного процесса 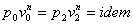можно получить уравнение для плотности: . Подставив полученное выражение уравнение для массовой скорости, получим: 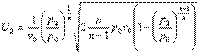или - уравнение массовой скорости для политропного процесса.

Уравнение массовой скорости для адиабатного процесса 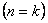будет иметь следующий вид: .

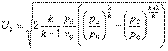Обычно отношение 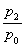обозначают за 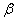. Коэффициент 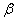лежит в пределах от 0 до 1 .

Графическое представление зависимости линейной и массовой скоростей от отношения давлений.

В зависимости от соотношений давлений возможны три режима:

1. До критический (дозвуковой) режим - .

2. Критический (звуковой) режим - .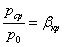

3. За критический (сверхзвуковой) режим - .

Для определения режима нужно знать значение . Для этого нужно найти экстремумы функции 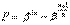. То есть , при .

Характеристика растяжения сжатия:

Для адиабатного процесса: , где - скорость звука.

Для идеального газа: .

Чтобы массовая скорость стала критической, то есть .

Массовый расход: .

Смешение потоков

Характер течения газа или пара зависит от формы неподвижных каналов и скорости потока. Особая роль принадлежит местной скорости звука, поэтому различают дозвуковой и сверхзвуковой режимы течения. Скорость звука определяется свойствами и параметрами газа:

Неподвижные каналы могут быть постоянного и переменного сечения. Последние делятся на суживающиеся и расширяющиеся. В вентиляционной технике они соответственно называются конфузорами и диффузорами, а в энергетике — соплами. Сопла — неотъемлемые элементы паровых и газовых турбин, реактивных и ракетных двигателей.

В суживающихся каналах (конфузоры, сопла) скорость потока возрастает, а давление падает, в расширяющихся — скорость может уменьшаться, а давление расти (диффузоры). Скорость может и увеличиваться при падении давления, если на входе обеспечивается скорость потока, равная местной скорости звука (расширяющиеся сопла).

Рассмотрим адиабатное течение потока (dq = 0) в неподвижном канале. Техническая работа в этом случае не производится (dl_T = 0). Из уравнений первого закона термодинамики (1.16) и (1.17) следует

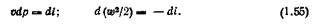
Интегрируя одно из уравнений (1.55) в пределах процесса 0—1 получим

С учетом уравнения адиабаты р^1/к v = const из выражения (1.55) найдем

Если w₁<<w₀, то выражение (1.56) упрощается.

В суживающихся каналах w₁≤a; для получения сверхзвуковых скоростей применяют комбинированные сопла (Лаваля), состоящие из суживающейся части, в которой скорость потока доводится до местной скорости звука, и расширяющейся части, где скорость потока становится сверхзвуковой.

При w₁<<a такой комбинированный канал называется эжектором. В наиболее узкой части его создается разрежение, за счет чего происходит подсос среды (пароструйные компрессоры, газовые горелки и пр.).

Критическая скорость истечения из суживающихся сопл w_K=a. Она достигается при некотором внешнем давлении р_к, чему соответствует определенное значение энтальпии i_к. Уменьшение давления среды, в которую происходит истечение, не даст прироста скорости; давление в выходном сечении такого сопла будет оставаться р_к.

Критическое отношение давлений β = р_кр/р_о можно вычислить из условия w_K=a:

Для одноатомных идеальных газов β = 0,484, для двухатомных— β = 0,528, для многоатомных газов и перегретого пара — β = 0,546; для насыщенного пара при t=100°С (к=1,18) отношение β = 0,568, при t=150 °С (к= 1,24) критическое отношение β = 0,556.

Секундный расход среды, кг/с, вытекающей из сопла сечением

Докритический режим течения существует при p_o<p₁/β, тогда в формулу (1.56) вместо p₁ подставляется давление внешней среды. Критический режим течения определяется давлением p_o=p₁/β. Если p_o>p₁/β, то полного расширения в сопле не наблюдается. Этот режим является закритическим. При критическом и закритическом режимах в формулы подставляются критические значения параметров i_K и v_K, найденные, например, по is-диаграмме вместо i₁ и v₁ (рис. 1.15).

Действительная скорость истечения всегда меньше теоретической из-за потери части кинетической энергии на преодоление сопротивления трения.

При набегании потока на какое-либо тело отдельные его струйки испытывают полное торможение. При этом кинетическая энергия потока уменьшается до нуля, за счет чего он нагревается до температуры полного торможения

Вопрос 49

Дросселирование (от нем. drosseln — душить) — понижение давления газа или пара при протекании через сужение проходного канала трубопровода —дроссель, либо через пористую перегородку.

Дата добавления: 2015-05-26