Абстрактний аналіз цифрових автоматів. Автомати Милі і Мура

Считайте, что этой книгой я по-дружески набрасываюсь на вас.

Бесконечный путь

Рынок меняется, возникают новые возможности, а старые исчезают. Хорошие игроки - люди преуспевающие, но скромные, они непрерывно учатся. Быть игроком - это дело всей жизни.

Я надеюсь, что эта книга поможет вам вырасти как игроку. Если вы дочитали до этого места, то, вероятно, серьезно относитесь к своей работе. Пользуясь этой книгой помните, что она является описанием того, что творится в уме у игрока и как он подходит к решению тех проблем, которые стоят перед всеми нами. Возьмите те ее идеи, которые вам нравятся, и приспособьте их к вашему стилю.

Если вы верите, что быть биржевым игроком - это достаточная награда за затраченные усилия, как я решил для себя годы тому назад, то я желаю вам всего лучшего. Я продолжаю учиться, как и любой игрок, и оставляю за собой право завтра стать умнее, чем сегодня.

В загальному вигляді для задання цифрового кінцевого автомата необхідно вказати:

- множину вхідних сигналів 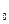X=(x , x 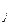.., x .., x );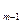

- множину вихідних сигналів Y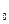=(у , у 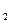, у .., у );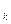

- множину станів автомат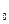а А=(а , а 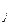.., а .., а );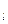

- функцію переходів f, що визначає стан автомата а (t+1) у момент дискретного часу t+1 залежно від стану автомата а (t) і значення вхідного сигналу x(t) у момент часу t:

- функцію виходів φ, що визначає залежність вхідного сигналу автомата у(t) від стану автомата і вхідного сигналу x(t) у момент часу t:

- початковий стан а .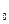

При записі функцій переходів і виходів іноді змінну t опускають, застосовуючи форми запису f(а, x) і φ(а,x). Представлену вище модель автомата називатимемо автоматом Милі

Таблиці переходів і виходів автомата Милі були приведені в попередній лекції (табл. 1, 2). Ці таблиці можна сумістити і одержати одну суміщену таблицю переходів-виходів автомата Милі ( див. табл. I)

Таблиця 1 - Суміщена таблиця переходів-виходів автомата Милі

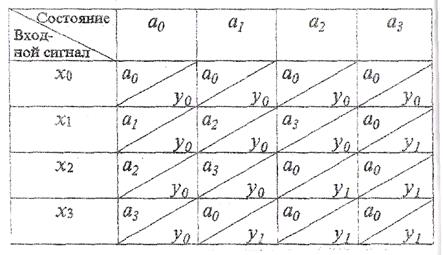
Окрім автоматів Милі, існують і інші типи автоматів, серед яких найпоширенішими є автомати Мура. Вони вирішують ті ж задачі, що і автомати Милі, але відрізняються від них внутрішньою структурою.

Функції переходів і виходів автомата Мура можна записати в наступному вигляді: а( t+1)=f(а,x) (1)

у(t)=φ(а) (2)

Ці функції звичайно задають таблицею переходів-виходів автомата Мура, яка будується так само, як і таблиця переходів Милі, але над символами кожного дискретного внутрішнього стану автомата Мура записуються вихідні сигнали, які задає автомат в даному стані (див. табл. 2

Таблиця 2 - Переходи-виходи автомата Мура

Відповідна табл.2 стрічка автомата Мура наведена в табл. 3

Таблиця 3 - Стрічка автомата Мура

Такти
Вхідний сигнал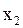
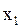
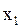
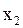
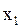
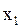
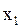
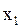
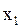
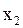
Стан
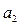
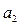
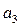
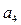
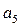
Вихідний сигнал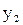

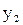
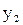
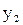
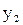
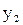
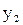
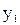
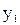
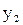
В ній жирною лінією виділена четвірка символів, яка показує, що автомат Мура під впливом сигналу x 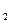, знаходячись в стані а 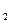, переходить в стан а 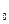, видаючи при цьому сигнал у 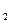на своєму виході.

Розглянуті автомати Мура і Милі називаються повними. Для них всі послідовності вхідних букв заборонені.

Проте існують автомати Мура і Милі, для яких деякі букви не можуть йти після попередніх, тобто існують заборонені вхідні слова.

Дата добавления: 2015-05-26