Краткая теория. Колебательную систему, состоящую из двух или более взаимосвязанных физических (математических) маятников называют связанными маятниками

Колебательную систему, состоящую из двух или более взаимосвязанных физических (математических) маятников называют связанными маятниками. Рассмотрим простейшую колебательную систему (рис.2), состоящую из двух одинаковых физических маятников, соединенных между собой невесомой пружиной с небольшой жесткостью k. Расстояния от точки подвеса до центра масс грузов одинаковы и равны L, а расстояние от точки подвеса до крепления пружины – l. Колебания маятников в вертикальной плоскости будут описываться двумя незави-симыми параметрами – углами φ₁ и φ₂ их отклонения от вертикали. Полагаем, что моменты сил трения и сопротивления, действующие на маятники, ничтожно малы и ими можно пренебречь. Тогда на маятники будут действовать только моменты силы тяжести и силы упругости. Векторы моментов силы тяжести направлены вдоль оси вращения «от нас», а их модули при малых (в пределах sin φ ≈ φ) колебаниях соответ-ственно равны:

- 4 -

Модули сил упругости, приложенные к обоим маятникам, одинаковы (см. рис.2) и равны 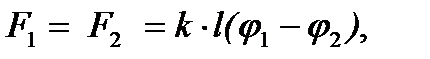а модули моментов силы упругости - (2)

Вектор момента силы упругости М₁ направлен вдоль оси вращения «от нас», а вектор момента силы упругости М₂ – «к нам», т.е. по направлению вектора углового перемещения φ₂.

С учетом (1) и (2) основное уравнение динамики враща-тельного движения 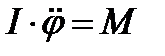применительно к каждому маятнику для малых колебаний имеет вид:

,

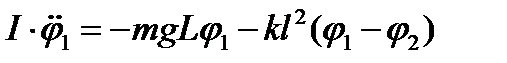. (3)

Систему уравнений (3) путем почленного сложения и вычита-ния уравнений с последующим делением на I и введением новых переменных 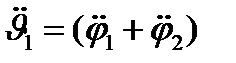и можно преобразовать к виду

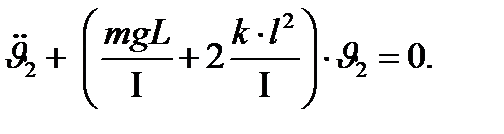(4)

Полученные уравнения (4) являются уравнениями колебаний гармонических осцилляторов с собственными частотами

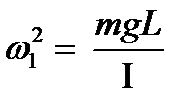и (5)

- 5 -

Общее решение уравнений (4) являются уравнения вида

Для удобства амплитуды угловых перемещений обозна-чены 2F₁и 2F₂, а начальные фазы - a₁ и a₂. Обратный переход к углам отклонения маятников позволяет установить зависимости φ₁(t) и φ₂(t):

(6)

Из уравнений (6) находим угловые скорости маятников:

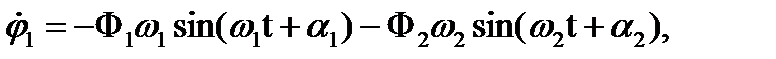
(7)

Таким образом, в общем случае колебания каждого маятника складываются из двух независимых колебаний с частотами w₁ и w₂, которые определяются выражениями (5) и носят название нормальных частот.

Как видно из уравнений (6), возможны случаи, когда оба маятника одновременно колеблются лишь с одной из нормальных частот (т.е. при Ф₁=0 или Ф₂=0). Каждая из возможностей осуществляется в зависимости от способа возбуждения колебаний в системе, т.е. от начальных условий (t=0). Начальные отклонения и угловые скорости маятников из (6) и (7) имеют вид:

- 6 -

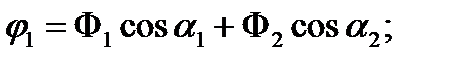
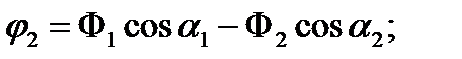
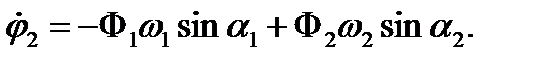(8)

Из уравнений (8) вытекают следующие выводы.

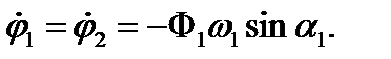1. Когда Ф₂=0, то в начальный момент оба маятника были откло-нены на один и тот же угол φ₁₀= φ₂₀=Ф₁cosaи имели одинаковые скорости

Этот случай соответствует так называемым синфазным колеба-ниям. Для получения синфазных колебаний маятники соединяют жесткой невесомой рейкой. Так как момент инерции связанных маятников увеличивается, то оба маятника колеблются с меньшей из нормальных частот w₁.

2. Случай Ф­₁=0 означает, что в начальный момент маятники были отклонены в противоположные стороны и имели противоположные скорости 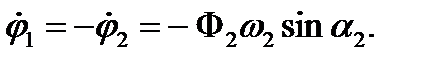При таком способе возбуждения оба маятника колеблются в противофазе с большей из нормальных частот w₂.

3. В общем случае произвольного способа возбуждения, каждый из маятников осуществляет сложное колебание, характер которого удобно наблюдать при слабой связи между маятниками: kl²<<mgL. Тогда разность Dw = w₂ - w₁ мала по сравнению с нормальными частотами и периодическое возрастание и убывание амплитуды колебаний каждого маятников происходит с частотой Dw. Такие колебания называют биениями.

- 7 -

На рисунке 3 приведены биения связанных маятников для расстояния от оси вращения до крепления пружины l =30 см. На зависимости U(t) отрезок времени между соседними узлами (или пучностями) является периодом биений Т_б. По периоду биений определим их циклическую частоту: Dw= 2π/ Т_б. (9)

Т_б

Рис.3. График биений.

Как следует из уравнений (5) изменение расстояния l от оси вращения до точки крепления пружины приведет к изменению циклической частоты w₂, а следовательно, и к изменению периода биений Т_б.

Дата добавления: 2015-05-26