Форми задання цифрових автоматів

Алфавітні оператори, що описують роботу цифрових автоматів, можуть бути представлені в різній формі. Найбільш простою і поширеною з них є таблиці переходів і виходів.

Ці таблиці (див. табл. 1, 2) містять стовпці станів, що позначаються , і стовпці змінних .

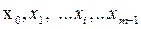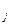В клітинку таблиці переходів, що знаходиться на перетині стовпця із станом а , і рядки з буквою x записується стан автомата а (t+1), в яке він перейде із стану а (t) при подачі на вхід сигналу 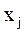у момент часу t.

В аналогічну клітину таблиці виходів записується вихідний сигнал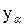

(α=0,1,..., к), який формується автоматом при такому переході.

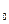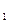В таблицях 1 і 2 заданий автомат, визначений на множині вхідних сигналів (x , x 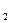, x , x 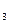), множині вихідних сигналів 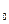(у , у 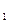) і множині внутрішніх станів .

Таблиця 1 –Переходи цифрового автомата

Вхідний сигнал	Стан

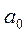
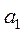
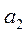
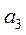
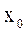
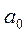
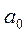
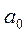
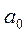
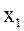
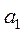
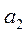
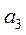
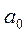
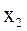
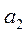
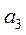
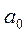
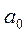
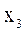
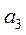
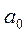
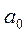
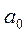
Таблиця 2 – виходи цифрового автомата

Вхідний сигнал	Стан

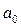
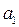
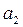
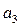
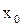
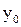
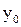
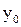
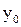
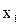
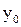
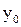
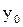
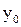
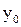
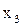
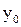
Автомат функціонує так, що кожного разу під час надходження послідовності букв вхідного алфавіту, сума індексів яких більше або дорівнює чотирьом, утворюється вихідний сигнал у 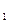. У всіх останніх випадках автомат утворює вихідний сигнал у 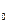. Під час надходження вхідного сигналу 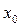автомат видає вихідну букву .

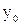По таблицях переходів і виходів можна знайти вихідну реакцію даного автомата на вхідне слово будь-якої довжини.

Робота автомата може представлятися за допомогою спеціальної таблиці 3, яку називають стрічкою цифрового автомата.

В будь-якому місці таблиці 3 можна виділити четвірку символів, як це показано в таблиці суцільною лінією. Ця четвірка показує, в який стан а 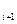перейде автомат, що знаходиться в стані а , і який виробляє вихідний сигнал 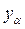під впливом вхідного сигналу.

Таблиця 3 – Стрічка автомата

Такт
Вхідний сигнал
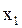
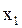
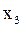
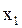
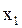
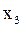
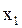
Стан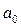
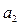
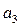
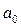
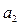
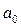
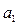
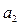
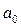
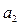
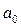
Вихідний сигнал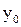

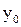
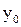
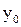
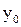
Велику наочність забезпечує завдання кінцевих автоматів за допомогою графів. Граф автомата складається з вузлів, сполучених гілками. Вузли графа ототожнюються з внутрішніми станами автомата Кожна гілка наголошується вхідним сигналом, що викликає в автоматі відповідний даній гілці перехід, і вихідним сигналом, який виникає при цьому переході. Кількість гілок, що виходять з будь-якого вузла графа автомата, рівна кількості букв вхідного алфавіту.

На мал. 1 зображений граф автомата, заданий таблицями I і 2.

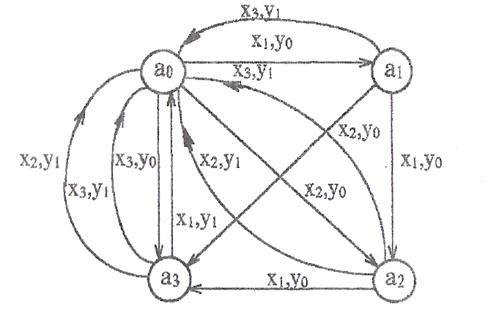
Малюнок 1 - Граф автомата

Зручність роботи з автоматом забезпечує уявлення його у вигляді дерева переходів і виходів. Воно містить два яруси, в пронумерованих вершинах першого з яких проставлені стани автомата, в які він переходить з початкового стану а 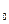під впливом вхідних сигналів x 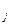, а в другому - стани автомата, в які він може перейти з будь-якого іншого стану.

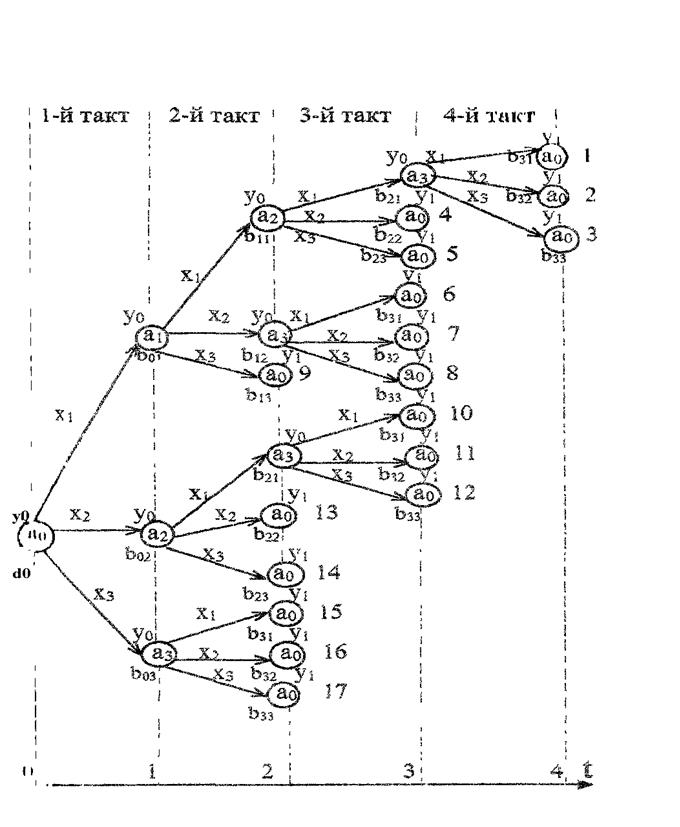
На мал. 2 зображено дерево для прикладу торгового автомата, що розглядається вище. Порожня буква x₀ і результат її дії на дереві не показано. Індекси i, j, b 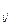показують індекс стану в якому автомат: i- знаходиться, індекс j – діючої вхідної змінної. Додатковою перевагою визначення автомата у вигляді дерева є можливість прослідити його роботу по тактах (див. мал. 3). З малюнка видно, що максимальне число тактів його роботи до переходу в початковий стан 4, а мінімальне – 2. В першому випадку треба кинути послідовно 4 монети гідністю 1 у.г.о., в другому - 2.

Так як автомат з кінцевою пам'яттю, як це видно з мал. 3, працює послідовно в часі по тактах, то такі автомати називають ще послідовними.

Комбінаційні автомати працюють на протязі одного такту і є окремим випадком автомата з кінцевою пам'яттю, що має один стан - а .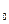

Мал. 2 – Дерево автомата з пам’яттю.

Мал.. 3 – Дерево роботи автомата з пам’яттю.

Н

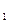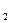На мал. 4 показано дерево роботи цього автомата для чотирьох вхідних букв x , x 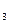, x , x 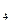. Відповідно до цього дерева під дією вхідного сигналу в момент часу t+1 залишається в початковому стані а 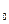і одноразово видає вихід сигналу , .

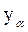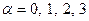Мал.. 4 – Дерево роботи комбінаційного автомата

Дата добавления: 2015-05-26