Сжатие сигнала

Представление сигнала регулярной выборкой отсчетов, получае­мой в результате его дискретизации, часто оказывается избыточ­ным. Сократить избыточность позволяют методы сжатия данных, суть которых заключается в уменьшении объема исходной инфор­мации путем отбора меньшего числа существенных координат. Эти координаты могут быть получены либо в результате некото­рого преобразования дискретного сигнала, либо выбраны непос­редственно из исходной выборки отсчетов. Чаще всего сжатие данных связано с некоторой потерей информации, из-за чего ис­ходный сигнал не может быть точно восстановлен.

Возможность получения эффективного сжатия сигнала связана с тем, что высокочастотные компоненты сигнала присутствуют на достаточно коротких отрезках времени. Частота дискре­тизации рассчитывается на допустимые ошибки дискретного пред­ставления именно этих фрагментов сигнала, поэтому описание регу­лярной выборкой отсчетов низкочастотных участков сигнала оказывается избыточным. Для устранения этой избыточности предложены различные методы сжатия, связанные с решением многих задач хранения, передачи и обработки сигнала.

Каждая из задач предъявляет свои требования к разрабатыва­емому методу сжатия и определяет его специфические особенно­сти, но общим требованием является получение достаточно эффек­тивного сокращения объема данных. Для оценки эффективности сжатого представления сигнала обычно применяют два показате­ля: коэффициент сжатия, определяемый отношением числа исход­ных отсчетов сигнала к числу полученных координат, и ошибка восстановления сигнала. В качестве последней чаще всего исполь­зуется абсолютная или средняя квадратическая ошибка. Подход к выбору метода сжатия и оценка его эффективности должен определяться конкретной целью его применения. В.задачах хранения и передачи данных обычно задается допустимый уровень искажения восстановленного сигнала, а выбор конкрет­ного метода осуществляется исходя из условий получения наилуч­шего значения коэффициента сжатия при известной или допусти­мой сложности реализации алгоритма кодирования-декодирования сигнала.

При использовании сжатия в качестве процедуры предвари­тельной обработки сигнала в КМ критерий верности восстановления сигнала не всегда доминирует. Часто основным фактором стано­вится возможность получения компактного описания, эффектив­но выявляющего структурные особенности анализируемого сигнала. Применяемый в этом случае метод сжатия должен сохранить об­раз обрабатываемой кривой, поскольку именно в нем содержится полезная информация, необходимая для распознавания сигнала. Кроме того, он должен отличаться высоким ко­эффициентом сжатия, простотой технической реализации и воз­можностью выбора координат в реальном масштабе времени.

Среди существующих методов сжатия данных можно выделить группу методов, основанных на разложении сигнала по ортого­нальным функциям. Применение для целей сжатия разложения Карунена-Лоэва, ряда Фурье, преобразования Хаара позволяет достигать высоких коэффициентов сжатия, однако требует боль­шого объема вычислений. Кроме того, возникает проблема пред­варительного выделения цикла, что затрудняет реали­зацию этих методов в системах реального времени. Такое сжатие используется для хранения сигнала в автоматизированных ар­хивах и передачи сигнала на расстояние, когда нет жестких требо­ваний к сложности алгоритмов обработки и скорости вычислений.

Широкое применение получили методы сжатия, основанные на амплитудно-временных преобразованиях сигнала. К наиболее про­стым относится метод разностного кодирования, который обеспечивает сокращение избыточности регулярной выборки отсче­тов за счет уменьшения объема каждой координаты. Принцип ко­дирования заключается в том, что для каждого i-гo отсчета сигнала u(t), u_i = u(t_i), поступившего на вход алгоритма сжатия, вычи­сляется разность значений соседних ординат (u_j — u_i-1), которая по модулю, как правило, меньше значений самих отсчетов, осо­бенно на участках сигнала с малой крутизной. Благодаря такому преобразованию удается уменьшить длину используемых слов, что приводит к сокращению объема памяти, необходимого для хране­ния и передачи сигнала. Важно отметить, что этот метод обеспечива­ет абсолютно точное восстановление дискретизованного сигнала. Если разрядность используемых кодовых слов значительно превы­шает разрядность вычисленных разностей, можно получить до­полнительное сжатие данных за счет более компактного их раз­мещения в информационном поле. Использование такого способа кодирования для хранения реализаций ЭКГ, представленных в виде последовательности отсчетов разрядностью 8—12 бит, сле­дующих с частотой 500 Гц, 16-разрядными словами, позволяет обеспечивать сокращение объема памяти более чем в 4 раза.

Достаточно распространены методы сжатия сигнала, исполь­зующие аппроксимацию сигнала на отдельных временных отрез­ках различными функциями. В качестве аппроксимирую­щих функций могут быть взяты алгебраические полиномы раз­ных степеней или специальные функции, но большинство алгорит­мов предполагает использование низкостепенных приближающих функций (ступенчатая или линейная аппроксимация). Это объяс­няется в основном их относительной простотой и высоким быстро­действием, что имеет решающее значение для задач передачи и обработки сигнала в реальном масштабе времени.

Среди методов описания сигнала специальными функциями из­вестен метод кодирования ЭКС нерегулярными отсчетами. Задача аппроксимации рассматривается здесь как определение оптимального набора восстанавливающих фильтров с выбором из них линейно-независимых, которые определяют номера сущест­венных отсчетов сигнала. Благодаря такому способу кодирования удается достичь коэффициентов сжатия порядка 15—20 в зависи­мости от сложности исходных кривых сигнала. Успешно применяют для сжатия ЭКС аппроксимацию сигнала кубическими сплайнами. Разработанный способ построения сглаживающего кубичес­кого, сплайна с адаптивным подбором шага на сетке узлов обес­печивает сокращение объема данных в 3—14 раз. Указанные мето­ды сжатия сигнала с применением специальных функций пред­ставляются перспективными для обработки сигнала в текущем режиме, однако в настоящее время считаются сложными для реализа­ции из-за большого объема вычислений.

Апертурные методы сжатия сигнала. Среди адаптивных методов приближения сигнала наибольший практический интерес предста­вляют апертурные методы, осуществляющие контроль абсолютной ошибки при определении избыточных отсчетов и выборе сущест­венных, т. е. передаваемых ординат. Они нашли широкое примене­ние в задачах оперативной передачи и обработки сигнала из-за высокого быстродействия и простоты реализации.

Принцип их действия заключается в последовательном продви­
жении по дискретным регулярным отсчетам u₀, u₁, u₂, … получен­ным после дискретизации непрерывного сигнала, до некоторого
n -го отсчета, в котором отклонение аппроксимированной ординаты от исходной превышает некоторое значение, задаваемое апер­турой d. Ордината u_n первой вышедшая за пределы коридора ши­риной d, принимается за условную существенную ординату. Кроме этого, вводится понятие существенной ординаты, используемой для передачи, обработки или восстановления сигнала. Выбор сущест­венной ординаты зависит от конкретной реализации алгоритма.

Во всех алгоритмах используется апертура, фиксированная по величин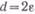е (, где - максимально допустимое отклонение) и центрированная относительно аппроксимирующей прямой ().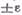

Наиболее прост в реализации метод сравнения дискретных отсчетов сигнала (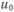, ,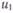..., ,...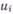) с фиксированными уровнями θ_k = kd, k = 0, 1, 2,..., при выбранном шаге квантования по уровню, равном d. Если для j -го участка аппроксимации, включающего п ординат, выполняется условие

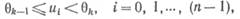(1)

а n-й отсчет условию (1) не удовлетворяет, то j -иучасток за­дается амплитудой 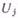и длительностью τ_j в виде

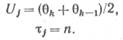
Здесь значения уровней θ_k = kd, k = 0, 1, 2,..., и соответственно облас­тей нечувствительности к отклонениям сигнала, задаваемым ин­тервалом 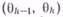, устанавливаются заранее исходя из выбран­ного значения d и не зависят от динамических свойств сигнала. Иллюстрация данного метода в графическом виде дана на рис. 13, где сплошной линией показана реализация сигнала, а также ее ступенчатая аппроксимация. Здесь, как и на последующих ри­сунках, кружками отмечены выборки, подлежащие передаче.

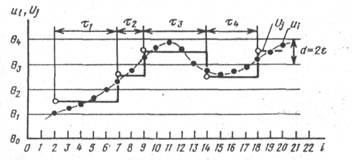Рис. 13. Сжатие сигнала методом сравнения с фиксированными уровнями

Более эффективны адаптивные процедуры апертурного сжатия, использующие плавающую апертуру d, которая на очередном участке аппроксимации устанавливается определенным образом относительно последней выбранной существенной ординаты сиг­нала, и таким образом отслеживается изменение амплитуды сиг­нала. Процедура поиска существенных ординат здесь определяется характером аппроксимации: интерполяцией или экстраполяцией. В качестве аппроксимирующих функций чаще применяют полино­мы нулевой, реже — первой степени.

Для плавающей апертуры выбор существенной ординатыпри поступлении каждого i-го отсчета в последовательности (u₀, u₁, …, u_i)осуществляется в результате сравнения разности опреде­ленных для конкретного алгоритма значений сигнала с аперту­рой d. Это условие для алгоритма экстраполяции нулевого по­рядка (ЭНП) имеет вид

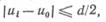(2)

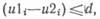а при использовании интерполяции нулевого порядка (ИНП) за­дается неравенством

(3)

где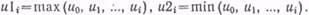

Если для i=п соответствующее условие нарушается, то (п —1)-й отсчет определяет конец текущего j-го участка аппроксимаций, а п-я выборка задает новое положение зоны допустимого отклонения значений сигнала шириной d. Из условий (2) и (3) следует, что положение плавающей апертуры при ЭНП фиксируется относи­тельно начальной ординаты 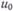, а при ИНП устанавливается лишь. с приходом (п —1)-го отсчета, вмещая в себя максимальное число избыточных отсчетов (рис. 14). Сжатое представление сигнала на j-м интервале аппроксимации для алгоритма ЭНП задается вели­чина.ми

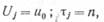a для алгоритма ИНП определяется выражениями

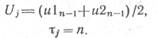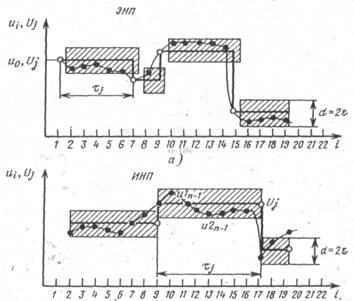Рис. 14. Экстраполяция (а) и интерполяция (б) сигнала алгебраическими полиномами нулевой степени

Апертурная аппроксимация сигнала может быть реализована также путем сравнения отсчетов сигнала с его представлением.алгебраическими полиномами первой степени. Использование более сложных функций затрудняет обработку сигнала в реальном вре­мени и не дает ощутимого выигрыша в коэффициенте сжатия.

В отличие от алгоритма ЭНП при экстраполяции.первого по­рядка (ЭПП) ось апертуры, являющаяся экстраполирующей прямой, располагается по линии, соединяющей первую ординату но­вого участка аппроксимации с предсказанным значением преды­дущей ординаты. Все отсчеты сигнала, попавшие в достроенный таким образом коридор, считаются (избыточными, а первый, вы­шедший за его пределы, начинает следующий участок аппрокси­мации. На выход алгоритма сжатия могут передаваться предска­занное значение последнего отсчета аппроксимирующей прямой и длительность соответствующего участка аппроксимации.

В алгоритме -интерполяции первого порядка (ИПП), в отличие от ЭПП, ось апертуры с приходом каждого следующего отсчета меняет свое положение. Вначале она проходит через первую и третью ординату текущего участка аппроксимации. Если второй отсчет попал в апертуру, то он считается избыточным. С прихо­дом следующего отсчета уравнение аппроксимирующей прямой будет задаваться уже первой и текущей ординатой, и так до тех пор, пока хотя бы одна из промежуточных ординат не выйдет за пределы коридора. Тогда текущая ордината начнет новый участок аппроксимации, а предыдущая вместе с параметром длительнос­ти будет передана на выход алгоритма сжатия.

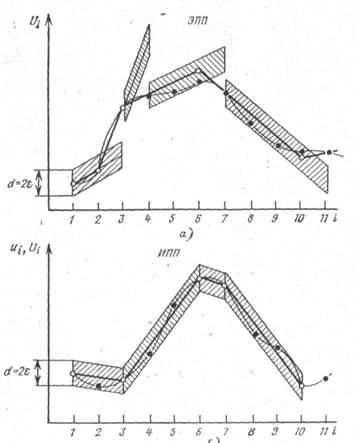
Графическая интерпретация алгоритмов сжатия ЭПП и ИПП приведена на рис. 15. Абсолютная ошибка восстановления дис­кретного сигнала не превышает величины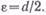

Плавающая апертура может задаваться постоянной, постоянной со сдвигом или переменной, что во многом определяет слож­ность и эффективность конкретного алгоритма сжатия.

Рис. 15. Экстраполяция (а) и интерполяция (б) сигнала алгебраическими полиномами первой степени

Из сравнительной оценки эффективности сжатия для ал­горитмов ЭНП, ЭПП, ИПП следует, что при коэффициентах сжатия, не превышающих 10, наиболее эффективным является алгоритм ИПП, а при допустимых уровнях искажений не более 10% - ЭНП.

Рассмотренные алгоритмы сжатия используют однопараметри­ческую адаптацию по интервалу аппроксимации, поскольку пос­ледний автоматически определяется при поиске существенных от­счетов. Дальнейшее повышение эффективности сжатия сигнала мо­жет быть достигнуто за счет использования двухпараметрической адаптации, позволяющей автоматически определять как длитель­ность интервала аппроксимации, так и степень аппроксимирую­щего полинома. При разработке алгоритмов анализа сигнала, осно­ванных на структурных методах, использующих сегментацию сиг­нала,.изменение порядка аппроксимации на отдельных его отрез­ках может 'стать информативным.признаком распознавания эле­ментов сигнала различной крутизны.

Дата добавления: 2015-05-26