Теоретическая часть. Определение теплоемкости металлов

Определение теплоемкости металлов

Лабораторная работа № 2

Цель работы:экспериментальное определение теплоемкости металла, сравнение с законом Дюлонга и Пти.

Теплоемкостью тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус:

.

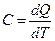Удельной теплоемкостью вещества называется теплоемкость единицы массы ве­щества:

Молярной теплоемкостью вещества называется теплоемкость массы вещества, равной молярной массе этого вещества:

, (1)

где m /m - количество молей вещества.

Величина теплоемкости зависит от условий нагревания. Процесс нагревания вещества при постоянном объеме характеризуется "теплоемкостью при постоянном объеме" с _v, а при постоянном давлении – "теплоемкостью при постоянном давлении" с_{р .} Для этих теплоемкостей всегда справедливо соотношение с_p > c _v – это доказывается с помощью термодинамических законов. Например, для идеального одноатомного газа молярные теплоемкости c _v = 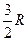, а с_р = .

Для твердых тел различие между этими теплоемкостями пренебрежимо мало, так как объем твердых тел при нагревании меняется мало ( при изменении температуры на 1 К). Поэтому говорят просто о теплоемкости твердого тела.

Из теории теплоемкости твердых тел, разработанной Эйнштейном и Дебаем, вытекают следующие важные положения, касающиеся поведения теплоемкости при низких и высоких температурах:

а) при стремлении абсолютной температуры к нулю теплоемкость тела также стремится к нулю

,

б) при температурах, существенно превышающих значение так называемой характеристической температуры Дебая Т _Д, молярная теплоемкость химически простых тел в кристаллическом состоянии есть величина постоянная, и равная

с _m = 3 R,

где R = 8,31 Дж/(моль×К) – универсальная газовая постоянная.

Последнее утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем и подтверждаемого классической статистической физикой. Действительно, из закона равномерного распределения энергии по степеням свободы следует, что на каждую степень свободы приходится энергии kT /2 ( - постоянная Больцмана). В кристаллическом состоянии атомы совершают малые колебания вблизи положения равновесия. На каждую колебательную степень свободы приходится энергия kT, равная сумме средних значений кинетической и потенциальной энергий. Число колебательных степеней свободы из кристалла, содержащего N атомов, равно 3 N. Поэтому средняя энергия теплового движения в кристалле равна 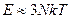. Соответствующая молярная теплоемкость равна

,

здесь N_А = 6,02×10²³ моль^-1 – постоянная Авогадро.

Теплоемкость кристаллов оказывается не зависящей от температуры и от конкретных свойств кристаллов.

Характеристические температуры Дебая некоторых кристаллов приведены в таблице 1.

Таблица 1

Кри­сталл	Pb	J	Na	Ag	NaCl	Cu	Al	Fe	Cr	Be	C (алмаз)
Т Д, К

Из приведенной таблицы характеристических температур следует, что для кристал­лов от свинца (Pb) и до поваренной соли (NaCl) комнатная температура (~ 300К) и бо­лее высокие темпе­ратуры являются сравнительно большими. Поэтому для подобных кристаллов отклоне­ния от закона Дюлонга и Пти в этой области температур не велики. Но, например, для бериллия и алмаза поведение теплоемкости при умеренных температурах совершенно отличается от закона Дюлонга и Пти. На рис.1 показана температурная зависимость теплоемкости кристалла меди.

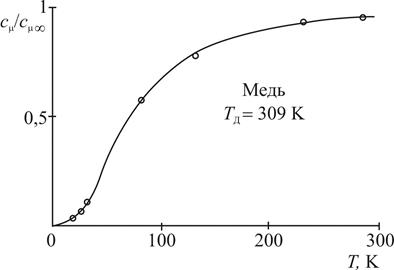Рис.1 Температурная зависимость теплоемкости меди

Дата добавления: 2015-05-26