Свойства аффинного пространства

1) Каждой паре совпадающих точек из A сопоставляется нулевой вектор из V.

Доказательство: Пусть М 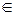A и = 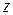. Пусть 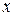- произвольный вектор из V 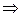//по аксиоме 2)//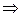 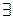точка N 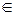A: 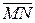= 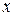. По аксиоме 1) + = + = = = = .■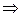

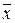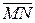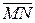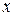
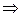
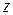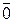2) Если 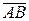= 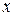, то = – .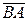

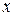Доказательство: Пусть = + = + = = = – . ■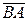

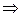
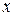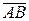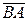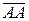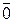
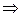
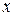Пример. Прямая, плоскость и пространство являются аффинными пространствами над векторными пространствами V , V , V .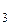

2˚. Аффинные координаты.

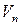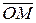
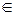
Рассмотрим n– мерное аффинное пространство A и введём в нём так называемую аффинную систему координат. Пусть О – точка в A – начало координат и пусть − базис в соответствующем пространстве . Пусть М – произвольная точка A . Тогда определён вектор 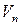, называемый радиус-вектором точки М. Разлагая 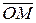по , имеем: .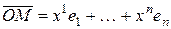

Коэффициенты этого разложения называются аффинными координатами точки М (относительно выбранной системы координат с началом в точке О и базисом ). Система {0, } называется репером.

Обозначение. .

Ввиду единственности разложения вектора по базису, координаты точки определяются однозначно.

Пусть дана другая точка N с координатами . Из аксиомы 1) аффинного пространства 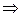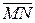= 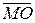+ 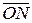= 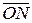− 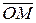= 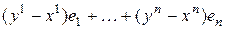, т.е. вектор 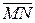имеет координаты ; т.е., чтобы получить координаты вектора 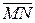надо из координат конца вычесть координаты начала.

Замечание 1. Пусть выбран базис и начало координат перенесено из точки О в точку О . Пусть координаты О в базисе с центром в О заданы координатами . Тогда имеем = + .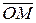

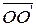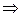
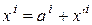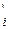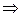Замечание 2. Если О = О , а базис { e } переходит в базис { e }: E = E X = X .

В общем случае, .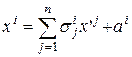

Дата добавления: 2015-05-29