Ошибки параллельных опытов

Каждый эксперимент содержит элемент неопределенности вследствие ограниченности экспериментального материала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и нужно оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов, если они имеют нормальное распределение. Среднее арифметическое y равно сумме всех n отдельных результатов, деленной на количество параллельных опытов n:

.

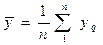Отклонение результата любого опыта от среднего арифметического можно представить как разность 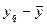, где 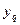— результат отдельного опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют исправленную дисперсию:

,

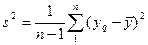где (n—1) — число степеней свободы, равное количеству опытов минус единица. Одна степень свободы использована для вычисления среднего. Корень квадратный из дисперсии, взятый с положительным знаком, называется средним квадратичным отклонением, или стандартным отклонением. Чем больше дисперсия и стандартное отклонение, тем больше рассеяны значения параллельных опытов около среднего значения.

Например, наличие резко отклоняющихся результатов (так называемых грубых наблюдений) свидетельствует о нарушении закона нормального распределения. При наличии грубых наблюдений нужно сначала их исключить, а затем подсчитывать среднее арифметическое и дисперсию.

Надо всегда следить, чтобы не нарушались необходимые условия выполнения той или иной операции. Иначе вы рискуете принять абсурд за истину. Ошибка опыта является суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь, разделить на составляющие. Вопрос о классификации ошибок довольно сложный и вызывает много дискуссий.

Все ошибки принято разделять на два класса: систематические и случайные (рисунок 2.1). Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и определить количественно. Систематические ошибки находят, калибруя измерительные приборы и сопоставляя опытные данные с изменяющимися внешними условиями (например, при градуировке термопары по реперным точкам, при сравнении с эталонным прибором). Если систематические ошибки вызываются внешними условиями (переменной температуры, сырья и т. д.), следует компенсировать их влияние. Как это делать, мы покажем в следующих параграфах.

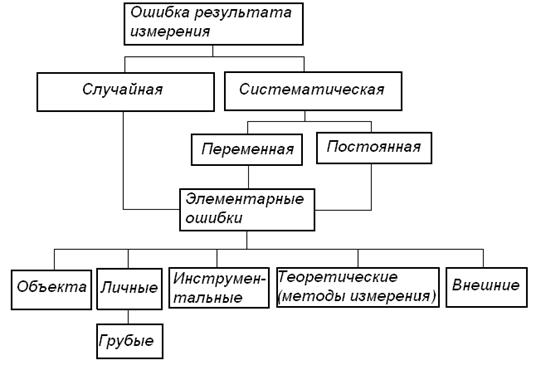
Рисунок 2.1 – Классификация ошибок измерения

Случайными ошибками называются те, которые появляются нерегулярно, причины возникновения их неизвестны, и которые невозможно учесть заранее. Систематические и случайные ошибки состоят из множества элементарных ошибок. Для того чтобы исключить инструментальные ошибки, если они имеют нормальное распределение, следует проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта. При повторении опытов такие ошибки могут вызвать большой разброс экспериментальных результатов. Как мы уже знаем, очень важно исключить из экспериментальных данных грубые ошибки, так называемый брак при повторных опытах. Ни в коем случае, конечно, нельзя вносить поправки самовольно.

При определения ошибочных опытов используют, например, критерий Стьюдента 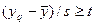. Значение t берут из таблицы t -распределения Стьюдента. Опыт считается бракованным, если экспериментальное значение критерия t по модулю больше табличного значения.

Пример. При исследовании процесса коррозии четыре повторных опыта показали следующие значения скорости коррозии:

3,580, 2,370, 2,710 и 2,761 мг/см^2 *час.

Результат первого опыта поставлен под сомнение, так как он выделяется на фоне остальных трех опытов. Исключив первый опыт из расчета, по остальным произведем вычисление среднего арифметического, стандартного отклонения и экспериментального критерия:

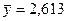, s= 0,21, .

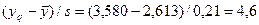При числе степеней свободы f=2 и уровне значимости a=0,05 табличное значение критерия равно t=4,303. Так как экспериментальное значение больше табличного, то сомнительный результат можно считать браком. Можно воспользоваться еще и другими критериями.

Пусть имеется n повторных наблюдений y1, у2,..., уn и возникает подозрение, что i -е наблюдение несовместимо с остальными. Подсчитаем среднее значение y и ошибку s. Найдем относительное отклонение для i -го наблюдения:

.

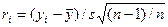Если найденное значение 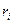для любого i -гo измерения не превосходит по абсолютной величине табличного значения 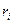для выбранного уровня значимости a и числа степеней свободы f = n—2, то можно принять гипотезу об однородности результатов наблюдений. При больших значениях числа степеней свободы r -распределение весьма близко к нормальному распределению.

В этих случаях для проверки однородности наблюдений можно пользоваться критерием трех сигма, полагая, что выборочная дисперсия хорошо характеризует генеральную дисперсию. Если ни одно из отклонений при большом числе измерений не превосходит по абсолютной величине Зs, то допустимо считать все наблюдения совместимыми. Критерий 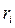применим для оценки любого i -ro наблюдения. Для оценки специально выбранных наблюдений, минимальных или максимальных, используется распределение максимального отклонения:

, .

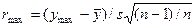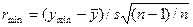В таблице 2.5 приведены значения 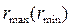для уровня значимости 0,01 и 0,05 и числах степеней свободы от 1 до 23.

Таблица 2.5 – Значения 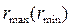для уровней значимости 0,01 и 0,05 [2].

Число степеней свободы	Уровень значимости	Число степеней свободы	Уровень значимости	Число степеней свободы	Уровень значимости
0,01	0,05	0,01	0,05	0,01	0,05
	1,414	1,412		2,606	2,343		2,932	2,600
	1,723	1,689		2,663	2,387		2,959	2,623
	1,955	1,869		2,714	2,426		2,984	2,644
	2.130	1,996		2,759	2,461		3,008	2,664
	2,265	2,093		2,800	2,493		3,030	2,683
	2,374	2,172		2,837	2,523		3,051	2,701
	2,464	2,237		2,871	2,551		3,071	2,717
	2,540	2,294		2,903	2,557

Если рассчитанное значение 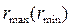превышает табличное, то оцениваемый результат может быть отнесен к грубым оценкам и не включаться в расчет. Предположим, что в первом опыте по экстракционному разделению циркония и гафния получены значения параллельных опытов: 12,15; 10,86; 16,00. Оценим последнее значение:

.

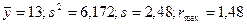Табличное значение 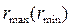для уровня значимости 0,05 и одной степени свободы равно 1,412. Наблюдение 16,00 может быть признано грубым. Здесь показаны самые простые приемы, которыми можно пользоваться при исключении ошибочных результатов [1, 2]. Возможны и другие приемы.

Отметим еще, что повторные опыты нельзя путать с повторными измерениями в одном опыте. Такие измерения часто делаются и являются полезными, но не могут заменить повторных опытов.

Дата добавления: 2015-05-26