
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Томографический эксперимент. Пример
|
|
|
|
Томография является очень характерным примером задач интерпретации эксперимента, принадлежащих к классу обратных задач. Томография применяется в самых различных областях науки - медицине (диагностика), физике твердого тела (неразрушающий контроль), геофизике (дистанционное зондирование) и т.д.
Рассмотрим постановочную часть типичной задачи томографии (рис. 1). Один из самых распространенных ее типов — это лучевая томография, основанная на геометрооптической физической модели переноса зондирующего излучения, что означает пренебрежение дифракционными эффектами. Типичный томографический эксперимент заключается в том. Что исследуемый образец «просвечивается» зондирующим излучением под разными углами, например, как это показано на рис.1. Для этого тем или иным способом организуется перемещение относительно образца передатчика и или приемника (на рис.1 они обозначены метками «tr» и «res» соответственно).

Рисунок 1. Иллюстрация принципа томографии
В ходе эксперимента обычно регистрируется определенная характеристика излучения, прошедшего через образец, например: амплитуда, фаза, разность фаз. Доплеровское смещение частоты или т.п. Излучение может быть акустическим или электромагнитным, в зависимости от выбранной технологии. Число траекторий также может быть различным. В частности, к показанным на рис.1 могут быть добавлены диагональные траектории или, напротив, сама специфика эксперимента может ограничивать их набор. Например, для геофизической томографии, использующей в качестве источников излучения искусственные спутники Земли (ИСЗ) характерен ограниченный набор траекторий (рис.2).
Ключевым моментом является интегральная зависимость указанной характеристики от исследуемых свойств образца. Например, пространственное распределение показателя поглощения в образце 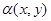 определяет ослабление интенсивности зондирующего излучения
определяет ослабление интенсивности зондирующего излучения  :
:
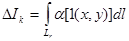 (1)
(1)

Рисунок 2. Геофизическая томография (веерная томография)
Символом 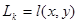 мы обозначили траекторию k-го луча. Таким образом, вклад в интеграл (1) (в общем случае, криволинейный) дает распределение
мы обозначили траекторию k-го луча. Таким образом, вклад в интеграл (1) (в общем случае, криволинейный) дает распределение 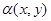 вдоль луча
вдоль луча  . Имея набор измерений (1) для серии траекторий
. Имея набор измерений (1) для серии траекторий 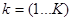 , можно попробовать реконструировать само поле
, можно попробовать реконструировать само поле 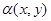 . Получается типичная обратная задача: записывая интеграл (1) в дискретном виде на пространственной сетке, которой покрывается образец, мы, в конечном счете, получим систему алгебраических уравнений вида:
. Получается типичная обратная задача: записывая интеграл (1) в дискретном виде на пространственной сетке, которой покрывается образец, мы, в конечном счете, получим систему алгебраических уравнений вида:
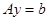 (2)
(2)
где в качестве неизвестного вектора 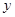 фигурирует массив значений
фигурирует массив значений 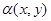 в узлах сетки. О самих принципах дискретизации будет написано ниже, на примере веерной томографии. Предполагается, что реконструируемое поте
в узлах сетки. О самих принципах дискретизации будет написано ниже, на примере веерной томографии. Предполагается, что реконструируемое поте 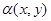 содержит информацию об исследуемой внутренней структуре образца (например, как правило, более плотные участки лучше поглощают излучение, а пустоты, напротив, имеют нулевое поглощение).
содержит информацию об исследуемой внутренней структуре образца (например, как правило, более плотные участки лучше поглощают излучение, а пустоты, напротив, имеют нулевое поглощение).
Если вспомнить, что при натурных измерениях всегда присутствует шумовая компонента (которая в данном случае складывается, по крайней мере, из погрешностей измерений и погрешностей дискретизации интеграла), то мы придем к уже хорошо знакомой линейной системе измерений:
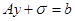 (3)
(3)
Рассмотрим теперь пример геофизической томографии (рис.2) и с его помощью разберемся, как осуществляется дискретизация задачи. В экспериментах по зондированию земной атмосферы на искусственном спутнике Земли (ИСЗ), движущемся по околоземной орбите, располагают передатчик электромагнитного излучения. На поверхности Земли находится один или множество приёмников, которые фиксируют тот или иной параметр пришедшей электромагнитной волны (например: амплитуду, фазу, поляризацию, угол прихода, частоту и т.п.).
Поскольку сигнал проходит в пространстве между спутником и приёмником путь в атмосфере, то в измеряемом параметре сигнала, в качестве которого, для определенности, выберем фазу 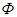 , содержится информация о состоянии атмосферы вдоль траектории луча. Соотношение между измеряемым параметром
, содержится информация о состоянии атмосферы вдоль траектории луча. Соотношение между измеряемым параметром 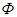 и интересующей характеристикой атмосферы, а именно, показателем преломления вдоль луча
и интересующей характеристикой атмосферы, а именно, показателем преломления вдоль луча 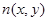 выражается интегральной зависимостью:
выражается интегральной зависимостью:
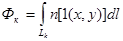 (4)
(4)
По-прежнему, через 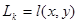 мы обозначаем траекторию
мы обозначаем траекторию 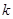 -го прямолинейного луча. Имея набор интегралов типа (4) для серии положений спутника в разные моменты времени, можно ставить задачу реконструкции
-го прямолинейного луча. Имея набор интегралов типа (4) для серии положений спутника в разные моменты времени, можно ставить задачу реконструкции 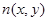 по серии экспериментальных данных. Таким образом, обращая данную систему интегральных уравнений относительно
по серии экспериментальных данных. Таким образом, обращая данную систему интегральных уравнений относительно 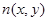 тем или иным вычислительным методом, можно получить решение как функцию показателя преломления пространственных координат. Для окончательной формулировки вычислительной задачи необходимо записать (4) в дискретном виде. Для этого производится разбиение атмосферы на конечные элементы (например, прямоугольные).
тем или иным вычислительным методом, можно получить решение как функцию показателя преломления пространственных координат. Для окончательной формулировки вычислительной задачи необходимо записать (4) в дискретном виде. Для этого производится разбиение атмосферы на конечные элементы (например, прямоугольные).
Мы будем использовать не прямоугольную систему координат 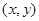 , а более естественную для сферически-симметричной Земли, ортогональную систему
, а более естественную для сферически-симметричной Земли, ортогональную систему  , в которой координатами являются криволинейное расстояние по поверхности Земли
, в которой координатами являются криволинейное расстояние по поверхности Земли 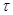 и высота над поверхностью Земли
и высота над поверхностью Земли 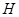 . Пусть в плоскости пролёта спутниканаЗемле расположено
. Пусть в плоскости пролёта спутниканаЗемле расположено 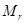 радиоприёмников. Их
радиоприёмников. Их
координаты равны 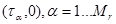 .
.
Начало координат  свяжем, ради определённости, с положением ИСЗ в момент старта зондирования и будем рассматривать промежуток высот
свяжем, ради определённости, с положением ИСЗ в момент старта зондирования и будем рассматривать промежуток высот  . Координаты орбиты спутникавкаждыймомент времени
. Координаты орбиты спутникавкаждыймомент времени 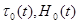 считаются заданными. Будем считать, что орбита ИСЗ - круговая, т.е.
считаются заданными. Будем считать, что орбита ИСЗ - круговая, т.е. 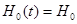 . Каждыйрадиоприёмникфиксирует всего
. Каждыйрадиоприёмникфиксирует всего 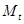 измерений в моменты времени
измерений в моменты времени 
Ценой смены системы координат будет потеря прямолинейности луча, уравнение траектории которого в системе координат  несложно получить путем геометрических преобразований:
несложно получить путем геометрических преобразований:
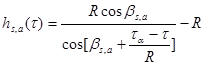 (5)
(5)
Соответственно, вместо интеграла (4) следует вычислять интеграл:
 (6)
(6)
Теперь для дискретизации задачи разобьем рассматриваемый слой атмосферы на 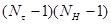 клеток, прямоугольных в
клеток, прямоугольных в  —координатах, в
—координатах, в 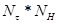 точках пересечения (узлах) которых показатель преломления
точках пересечения (узлах) которых показатель преломления 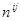 , где
, где 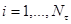 и
и  подлежит
подлежит
реконструкции.
Итак, мы определились со значением  в узлах сетки. Осталось указать, чему равна эта функция в других точках пространства между узлами. Очевидно, что выразить её необходимо тем или иным образом через значение
в узлах сетки. Осталось указать, чему равна эта функция в других точках пространства между узлами. Очевидно, что выразить её необходимо тем или иным образом через значение 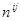 в ближайших к данной точке узлах. На рис.3 изображен
в ближайших к данной точке узлах. На рис.3 изображен 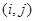 —й (по индексу верхнего левого узла) элемент сетки
—й (по индексу верхнего левого узла) элемент сетки  .
.

Рисунок 3. Сетка
Для того чтобы наиболее просто определить значение  в каждой точке
в каждой точке  этого конечного элемента, можно просто считать, что
этого конечного элемента, можно просто считать, что 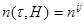 . Такая аппроксимация называется кусочно-постоянной. Ошибка при этом имеет порядок пространственного шага, а интеграл (6), соответственно, будет рассчитываться методом прямоугольников. Такая точность редко бывает достаточной. Поэтому необходимо использовать более высокий порядок аппроксимации, например, кусочно-планарную. В этом случае функция
. Такая аппроксимация называется кусочно-постоянной. Ошибка при этом имеет порядок пространственного шага, а интеграл (6), соответственно, будет рассчитываться методом прямоугольников. Такая точность редко бывает достаточной. Поэтому необходимо использовать более высокий порядок аппроксимации, например, кусочно-планарную. В этом случае функция  внутри каждой клетки заменяется линейной функцией по каждой переменной:
внутри каждой клетки заменяется линейной функцией по каждой переменной:
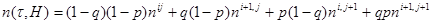 (7)
(7)
где
 ,
,  (8)
(8)
Ещё меньшую погрешность даёт кусочно-квадратичная аппроксимация по шести точкам, когда функция  заменяется кривой второго порядка и т.д. Существует множество способов аппроксимировать
заменяется кривой второго порядка и т.д. Существует множество способов аппроксимировать  , каждый из которых приведёт, в итоге, к определению своей матрицы
, каждый из которых приведёт, в итоге, к определению своей матрицы 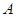 . Выбрав вид аппроксимации, несложно завершить процедуру построения матрицы
. Выбрав вид аппроксимации, несложно завершить процедуру построения матрицы 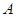 . Для этого остается подставить аппроксимацию (7) в интеграл (6) и подсчитать эти интегралы во всех клетках, в которых побывает
. Для этого остается подставить аппроксимацию (7) в интеграл (6) и подсчитать эти интегралы во всех клетках, в которых побывает  -ый луч, рассматривая
-ый луч, рассматривая 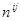 в качестве неизвестных коэффициентов пропорциональности. Аналитически интегралы (6) в данном случае не берутся, поэтому их приходится считать каким-либо численным методом, например, Симпсона. Потом следует сгруппировать подобные слагаемые при каждом
в качестве неизвестных коэффициентов пропорциональности. Аналитически интегралы (6) в данном случае не берутся, поэтому их приходится считать каким-либо численным методом, например, Симпсона. Потом следует сгруппировать подобные слагаемые при каждом 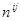 , чтобы в итоге получить соотношение:
, чтобы в итоге получить соотношение:
 (9)
(9)
в котором в матрицу (точнее, тензор) F заложены численные значения соответствующих интегралов (6) при 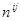 Таким образом, мы сформировали модель
Таким образом, мы сформировали модель  . Представляющую математическую постановку задачи веерной томографии.
. Представляющую математическую постановку задачи веерной томографии.
Четыре индекса элементов матрицы  в (9) выражают, соответственно, номер луча, номер приемника, а также
в (9) выражают, соответственно, номер луча, номер приемника, а также 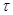 - и
- и 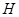 - координаты клетки. Для упрощения их удобно перенумеровать:
- координаты клетки. Для упрощения их удобно перенумеровать:
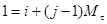 ,
, 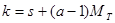 (10)
(10)
Где 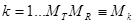 ,
, 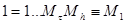
Итак, мы наконец пришли к формулировке вычислительной задачи - решения 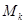 линейных уравнений относительно
линейных уравнений относительно 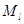 неизвестных.
неизвестных.
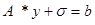 (11)
(11)
После того, как задача математически полностью сформулирована, остаётся выбрать алгоритм её решения. Эти алгоритмы, преимущественно, являются итерационными, ввиду большой размерности задачи. Например, весьма эффективный и экономичный метод заключается в замене системы уравнений (11) системой линейных неравенств:
 (11+)
(11+)
Допустимая погрешность 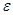 может быть согласована с уровнем шума
может быть согласована с уровнем шума 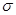 (если последняя известна). Алгоритмы численного решения (11+) основаны на выборе нулевой итерации вектора
(если последняя известна). Алгоритмы численного решения (11+) основаны на выборе нулевой итерации вектора 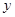 (из некоторых априорных соображений) и дальнейшем последовательном вычислении невязок уравнений в целях соответствующей корректировки текущего приближения
(из некоторых априорных соображений) и дальнейшем последовательном вычислении невязок уравнений в целях соответствующей корректировки текущего приближения 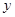 . Завершим параграф несколькими конкретными примерами моделирования прямой задачи (6). На рис. 4-7, полученных при помощи программы Tomography Calculator изображены, соответственно, модельное поле
. Завершим параграф несколькими конкретными примерами моделирования прямой задачи (6). На рис. 4-7, полученных при помощи программы Tomography Calculator изображены, соответственно, модельное поле  , схема эксперимента, расчет интегральных характеристик зондирующего луча и результат реконструкции.
, схема эксперимента, расчет интегральных характеристик зондирующего луча и результат реконструкции.

Рисунок 4. Модельное поле 

Рисунок 5. Модель эксперимента. Программа tomography calculator.

Рисунок 6. Модельные измерения (в 2х точках, кривые) и погрешность аппроксимации (точки).

Рисунок 7. Результаты реконструкции поля  (алгоритм ART 3)
(алгоритм ART 3)
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 640; Нарушение авторских прав?; Мы поможем в написании вашей работы!