Метод Фибоначчи

Метод дихотомии

Метод поразрядного приближения

Метод равномерного поиска

Методы оптимизации функций одной переменной

Этот метод основан на том, что переменной x присваиваются значения x+∆x с шагом ∆x = const и вычисляются значения F(x). Если F(x _n+1)>F(x_n), переменной x даётся новое приращение. Как только F(x_n+1)станет меньше F(x) поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.

Этот метод является разновидностью метода равномерного поиска и реализуется следующим алгоритмом:

1. Задаём начальное приближение x=x₀ слева от максимума F(x) и вычисляем F(x₀). Задаём D=h, где h=∆x – начальный шаг поиска.

2. Полагаем, что G=F(x_n), где вначале F(x_n)=F(x₀), задаём x=x+D и вычисляем F(x _n+1)=F(x).

3. Проверяем условие F(x n₊₁)>G; если оно выполняется, идём к п.2, если нет, то к п.4.

4. Полагаем D=-D/4. Проверяем условие |D|>E/4, где E – заданная погрешность вычисления x_n в точке максимума. Если оно выполняется, идём к п.2, т.е. обеспечиваем поиск максимума в другом направлении с шагом в 4 раза меньше прежнего. Если данное условие выполняется, процесс вычисления заканчиваем.

Метод дихотомии (деление интервала поиска [a, b] пополам) реализуется следующим алгоритмом:

1. Проверяем условие |b-a|<2E, где E – заданная погрешность вычисления x_n. Если это условие выполняется, идём к п.6; если не выполняется, идём к п.2.

2. Делим интервал поиска [a, b] пополам и вычисляем две абсциссы, симметрично расположенные относительно точки

x=(a + b)/2

x₁=(a + b - E)/2 и x₂=(a + b + E)/2

3. Для этих значений x вычисляем F(x₁)>F(x₂).

4. Проверяем условие F(x₁)>F(x₂). Если оно выполняется, полагаем b=x₂ и идём к п.1. Если не выполняется, идём к п.5.

5. Полагаем a=x₁ и идём к п.1.

6. Выводим на печать x_n=(a+b)/2 и вычисляем F(x_n).

В методе Фибоначчи точка деления интервала исследования определяется с каждым новым расчётом (в методе дихотомии необходимо на каждом шаге выполнять два расчёта). В интервал исследования попадет предыдущий расчёт и для продолжения поиска достаточно произвести расчёт симметрично имеющемуся.

Допустим, задано число расчётов (шагов) N. Необходимо их произвести так, чтобы интервал, в котором лежит оптимум, был минимальным. Числа Фибоначчи, используемые в этом методе, определяются следующим образом:

F_N=F_N-1+F_N-2

F₀=F₁=1

Алгоритм метода Фибоначчи состоит из следующих этапов:

1) Изменяют масштаб исходного интервала, в котором лежит оптимум. В качестве единицы измерения принимают 1=X₀/F_N, или если задана длина l, в котором лежит оптимум, находят его на исходном интервале длиной X₀. Для этого, разделив X₀ на 1, находят ближайшее большее число Фибоначчи F_N,
а по нему определяют N – число необходимых расчётов для определения интервала.

2) Расставляют первые две точк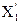и и 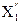на интервале исследования X₀ на расстоянии F_N-2 от конца b.

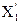3) Вычисляют значение целевой функции в этих точках для сужения интервала исследования. Пусть > , тогда интервал [ , F_N] исключается из рассмотрения.

4) На новом интервале исследования снова расставляют две точки и 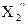, но в одной из них уже известно значение целевой функции = .

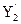5) Переходят к этапу 3 и т.д., пока не достигают искомого интервала, в котором находится значение переменной, максимизирующее её целевую функцию.

На рис. 6 показан процесс сужения интервала исследования:

Рис. 6. Процесс сужения интервала исследования.

Последний N–й расчёт определяет интервал длиной l, в котором находится экстремум целевой функции.

Дата добавления: 2015-05-29