
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производные и дифференциалы высших порядков. Правило Лопиталя
|
|
|
|
Практическая работа № 16
Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
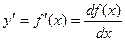
Если найти производную функции f¢(x), получим вторую производную функции f(x).
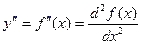
т.е. y¢¢ = (y¢)¢ или  .
.
Этот процесс можно продолжить и далее, находя производные степени n.
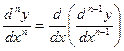 .
.
Пример 1. Найти производную второго порядка функции 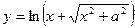
Решение.
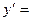
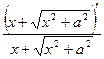
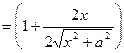
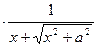
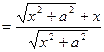
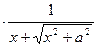
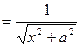
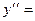
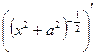
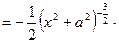

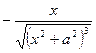
 Пример 2. Найти третью производную от функции
Пример 2. Найти третью производную от функции 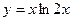 в точке
в точке 
Решение.
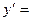


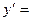

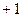
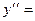


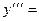

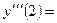
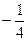
 Пример 3. Вычислить значения первой и второй производных функции
Пример 3. Вычислить значения первой и второй производных функции 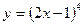 в точке
в точке 
Решение.
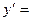
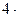
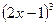
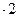
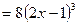

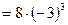

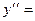

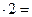
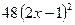
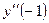
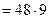

Пример 4. Найти 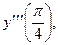 если
если 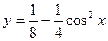
Решение.
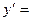
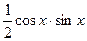
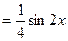
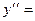
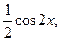
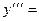
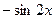
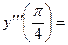
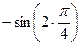
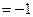
Пример 5. Найти производную  порядка функции
порядка функции 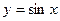
Решение.
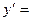
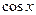
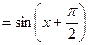
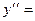

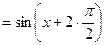
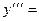
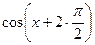
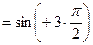
…………………………
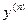
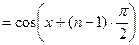
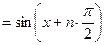
 Пример 6. Записать формулу для производной
Пример 6. Записать формулу для производной  порядка, если
порядка, если 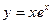
Решение.
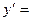
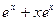
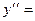
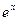
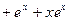
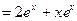
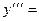
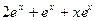
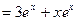
…………………………
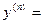
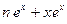
Пример 7: Точка движется прямолинейно по закону 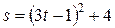 . Вычислить скорость и ускорение в момент времени
. Вычислить скорость и ускорение в момент времени 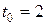 .
.
Решение:
Скорость: 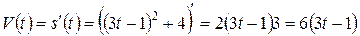 .
.
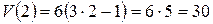 (ед. скорости).
(ед. скорости).
Ускорение:  .
.
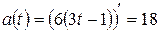 .
.
Т.е ускорение постоянно в любой момент времени, следовательно, 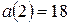 ед. ускорения.
ед. ускорения.
 Пример 8. Найти дифференциал второго порядка функции
Пример 8. Найти дифференциал второго порядка функции 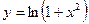
Решение.
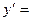

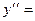
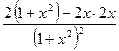
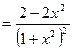
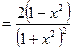
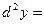
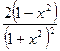
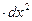
Дифференциал сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f¢(x)g¢(t)dt = f¢(x)dx.
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если х- независимая переменная, то
dx = Dx, но
если х зависит от t, то Dх ¹ dx.
Таким образом форма записи dy = f¢(x)Dx не является инвариантной.
Пример. Найти производную функции 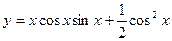 .
.
Сначала преобразуем данную функцию: 
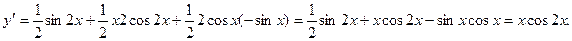
Пример. Найти производную функции 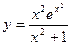 .
.
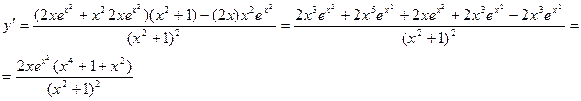
Пример. Найти производную функции 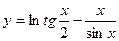
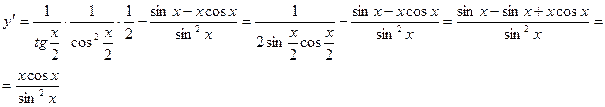
Пример. Найти производную функции 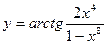
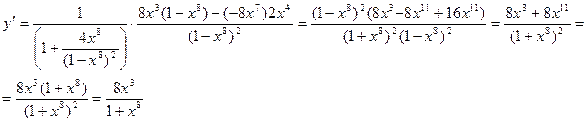
Пример. Найти производную функции 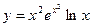

Применение дифференциала к приближенным вычислениям.
Дифференциал функции y = f(x) зависит от Dх и является главной частью приращения Dх.
Также можно воспользоваться формулой
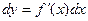
Тогда абсолютная погрешность
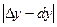
Относительная погрешность
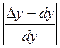
Приближенные вычисления с помощью полного дифференциала.
Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:
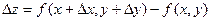

Если подставить в эту формулу выражение
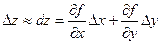
то получим приближенную формулу:
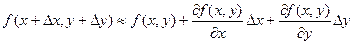
Пример. Вычислить приближенно значение  , исходя из значения функции
, исходя из значения функции 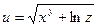 при x = 1, y = 2, z = 1.
при x = 1, y = 2, z = 1.
Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01,
Dz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) = 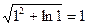
Находим частные производные:
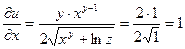
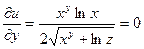
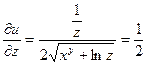
Полный дифференциал функции u равен:
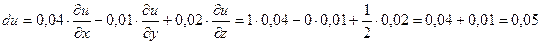

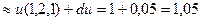
Точное значение этого выражения: 1,049275225687319176.
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

Пример 1. Найти 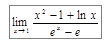 .
. 
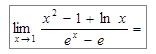
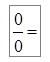
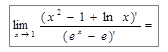

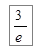 .
.
Пример 2. Найти 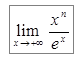 .
.
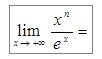
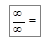
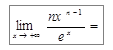
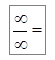
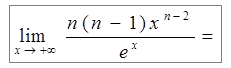
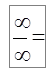 …
… 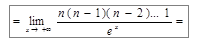

Пример 3. Найти 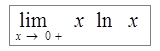 .
.
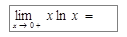



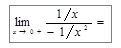
 .
.
Пример 4: Найти предел 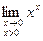 .
.
Здесь 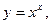
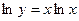
Тогда  . Следовательно
. Следовательно 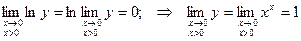
Пример5: Найти предел 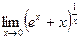 .
.
Решение.

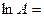
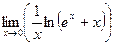
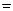
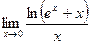
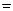
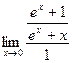

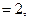
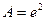
Пример 6. Найти 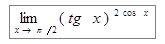 .
.
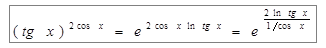
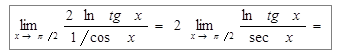
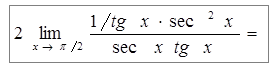
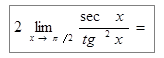
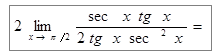


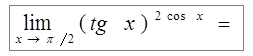

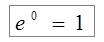
Пример 7: Найти предел 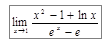 .
.
Как видно, при попытке непосредственного вычисления предела получается неопределенность вида 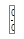 . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
f¢(x) = 2x +  ; g¢(x) = ex;
; g¢(x) = ex;
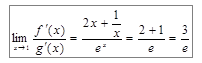 ;
;
Пример 8: Найти предел 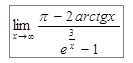 .
.
 ;
; 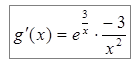 ;
;
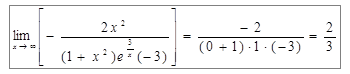 .
.
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Пример 9: Найти предел  .
.
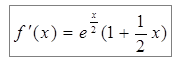 ;
; 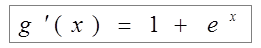 ;
;
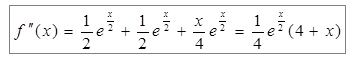 ;
; 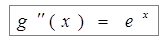 ;
;
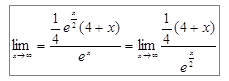
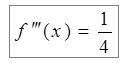 ;
; 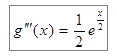 ;
; 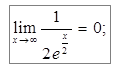
Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
Пример 10: Найти предел 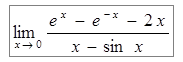 .
.
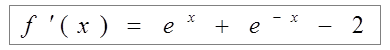 ;
; 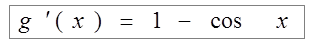 ;
;
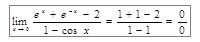 - опять получилась неопределенность. Применим правило Лопиталя еще раз.
- опять получилась неопределенность. Применим правило Лопиталя еще раз.
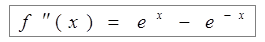 ;
; 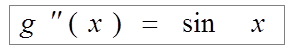 ;
;
 - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз.
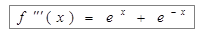 ;
;  ;
;
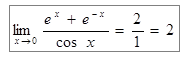 ;
;
Неопределенности вида 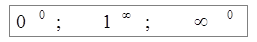 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 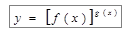 , f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
Пример 11: Найти предел 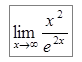 .
.
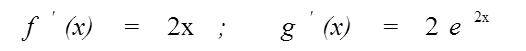 ;
; 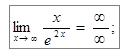 - получили неопределенность. Применяем правило Лопиталя еще раз.
- получили неопределенность. Применяем правило Лопиталя еще раз.
 ;
; 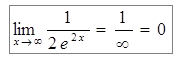 ;
;
Задания
1) 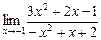
2) 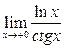
3) 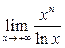 ;
; 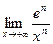 ;
;
4 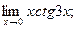
5)  ;
;
6) 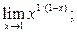
7) 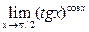
8) 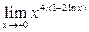
9) 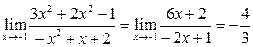
10) 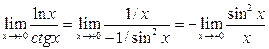
11) 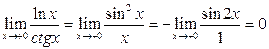
12) 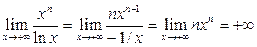
13) 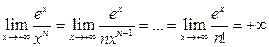
14) 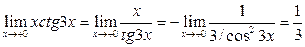
15) 
16) 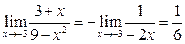
17) 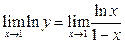
18) 
19) 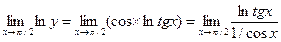
20) 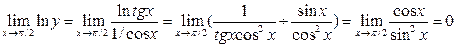
21)  ;
; 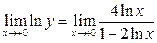
22) 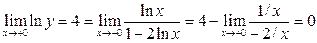
|
|
|
|
Дата добавления: 2015-05-31; Просмотров: 1059; Нарушение авторских прав?; Мы поможем в написании вашей работы!