Определение математических зависимостей между параметрами по результатам экспериментальных исследований

В ряде случаев приходятся определять значение

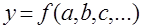
по результатам измерений других величин 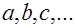(косвенные измерения). Определяя погрешность величины 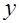, здесь пользуются следующими правилами. Если функция 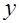представляет собой сумму слагаемых, то относительная погрешность принимается равной среднеарифметической погрешности слагаемых. Относительная погрешность произведения либо частного равна сумме относительных погрешностей сомножителей, числителя и знаменателя. Относительная погрешность степени равна ошибке основания, умноженной на показатель степени и деленной на основание. Относитель­ная погрешность косинуса и синуса равна произведению значений тангенса и котангенса на предельную абсолютную погрешность угла в радианах. Относительная погрешность тангенса и котангенса равна частному от деления двойной абсолютной погрешности угла на синус двойного угла.

Рассмотрим методы поиска функциональных зависимостей. Пусть требуется экспериментальный путем установить вид функции

.

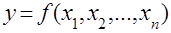Следует помнить, что для решения этой задачи требуемое число опытов находится в степенной зависимости от числа аргументов 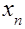. Поэтому необходимо попытаться сократить число переменных в искомой функции, выделив наиболее значимые, используя методы теории подобия и размерностей.

Предположим, что задача свелась к установлению вида функции от одной переменной. Теперь следует решить вопрос о пределах изменения аргумента (фактора). Это определяется конкретными условиями задачи. Следует иметь в виду, что узкая область изменения фактора обеспечивает получение более точкой математической зависимости, однако утрачивается общность полученных результатов. Далее необходимо определить число опытов и шаг изменения фактора. Практика показывает, что в большинстве случаев достаточна постановка опытов при пяти значениях фактора, выбранных в заданной интервале с равным шагом. Число опытов для каждого значения фактора определяют так же, как и при измерениях случайной величины. Располагая результатами эксперимента, точки наносят на график и проводят плавную кривую, которая по возможности должна проходить через все средние точки. Могут иметься изгибы и перегибы кривой; в таких областях необходима постановка не менее трех дополнительных экспериментов. Имея экспериментальную кривую, приступают к подбору соответствующей математической зависимости – эмпирической формулы.

Точный и общий метод определения параметров искомой функции – способ наименьших квадратов. В общем случае его применяют для поиска функций в виде степенного многочлена

.

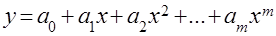Коэффициенты 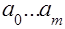могут быть найдены по результатам активного или пассивного эксперимента.

Широкое распространение при проведении экспериментальных исследований получили планы многофакторных экспериментов, позволяющие изменять одновременно уровень нескольких факторов согласно плану эксперимента.

В данном случае число опытов сокращается до минимума, однако на изменение факторов в ходе эксперимента накладываются определенные ограничения. Известны ортогональные, рототабельные и другие планы экспериментов. При выполнении научно-исследовательской работы наиболее удобны ортогональные планы. В этом случае, используя соотношения

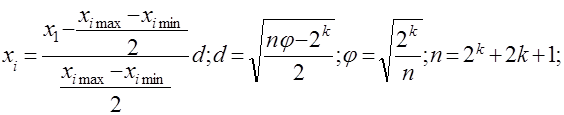
зависимость от натуральных значений факторов преобразуют в зависимость от факторов в кодированной (безразмерной) форме:

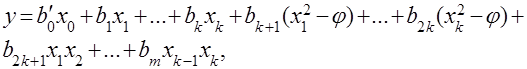
где 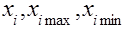– значение 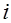-го фактора соответственно текущее, максимальное и минимальное; 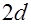– плечо изменения факторов в кодированной форме (область изменения факторов определяется пределами 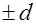; 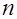– число однократных опытов, заданных планом, общее число опытов 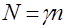, где 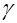– повторность опытов, принимается равной 2 или3; 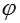– коэффициент; 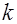– число факторов.

Для определения коэффициентов регрессии 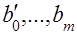необходимо реализовать план эксперимента, приведенный в табл. 2 (ортогональный план двухфакторного эксперимента приведен в табл. 3), где фактор 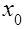введен условно, значение его во всех строчках плана равно +1.

Таблица 2

Ортогональный план эксперимента

Номер опыта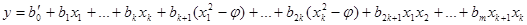
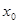
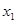
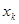
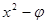
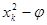
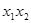
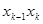
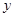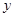
	+1	+1	+1	1-	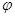1-	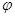+1	…	+1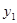
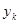
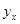
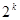
	+1	+1	–1	1-	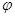1-	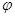–1	…	–1
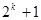
	+1						…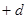
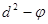
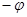
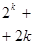
	+1						…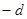
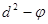
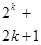
	+1

Таблица 3

Ортогональный план двухфакторного эксперимента

Номер опыта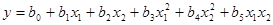
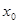
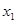
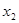
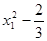
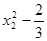
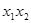
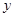
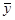
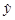
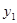
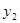
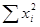
	+1 +1 +1 +1 +1 +1 +1 +1 +1	–1 +1 –1 +1 –1 –1	–1 –1 +1 +1 –1 +1	1/3 1/3 1/3 1/3 1/3 1/3 –2/3 –2/3 –2/3	1/3 1/3 1/3 1/3 –2/3 –2/3 1/3 1/3 –2/3	+1 –1 –1 +1

В первых строчках плана от 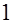до 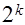факторы 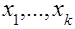, составляют различные комбинации значений +1 и –1. В строчках плана 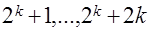каждый фактор последовательно принимает значения 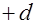и 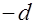, при этом все остальные факторы равны нулю. Последовательность постановкиопытовможет быть случайной.

Искомые коэффициенты регрессии определяются соотношением

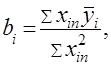
где 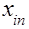– кодированные значения фактора для столбца, в плане эксперимента, соответствующего искомому коэффициенту; 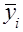– среднее арифмети­ческое значение искомой величины, полученное по результатам измерений величин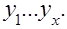

Далее вычисляют коэффициент 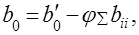( 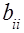– значение коэффициента при квадратичных факторах) и переписывают уравнение регрессии в виде

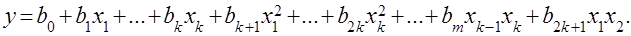Ошибка опыта (дисперсия воспроизводимости)

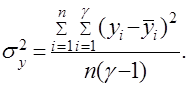
Дисперсия коэффициентов

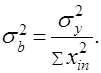
Исходя из этого, определяют значимость коэффициентов,которые должны быть больше действительного интервалаих изменения:

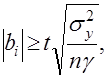
где величина принимается по таблице в зависимости от числа степе­ней свободы дисперсии воспроизводимости

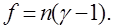
Далее проверяют адекватность искомой функции результатам эксперимента.

Дисперсия адекватности

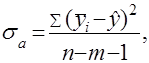
где 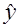– расчетное значение величины, определяемое по полученной за­висимости, 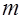– число искомых коэффициентов.

Число степеней свободы дисперсии адекватности

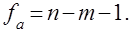
Адекватность проверяют по критерию Фишера

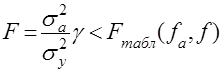. (2)

Далее, используя соотношения, переходят от найденного урав­нения регрессии в кодированной форме к искомой зависимости в натуральных переменных. Если условие (2) не выполняется, следует перейти к полиному более высокой степени либо сузить пределы изменения факторов. Иногда достаточно найти зависимость в виде линейного полинома. Здесь ограничиваются постановкой опытов, определяемых строчками плана 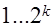. Дальнейшая обработка данных остается такой же.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каким образом оценивается точность измерений?

2. Как определяется результат измерения и его точность?

3. Каким образом определяется необходимое число опытов?

4. Каким образом определяется функциональная зависимость по результатам опытов?

5. Методика построения ортогонального плана эксперимента.

6. Методика определения коэффициентов регрессии и их значимости.

7. Методика проверки адекватности искомой функции результатам эксперимента.

Дата добавления: 2015-05-26