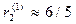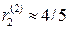И сотрудничества

Матричная игра как модель конкуренции

Пусть игроки – Первый и Второй, играют в матричную игру с матрицей 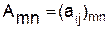. Пусть стратегия Первого есть Р = (p_1, p_{2, …,} p_m), где p_i – вероятность выбора i-ой строки, а Второго – Q = (q_1, q_{2, …,} q_n), где q_j – вероятность выбора j-го столбца. Тогда выигрыш Первого есть случайная величина (с.в.) 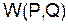с рядом распределения:

W(P,Q)			…				…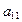
			…				…

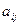
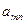
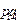
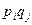
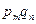
Математическое ожидание этой с.в., т.е. 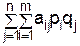есть средний выигрыш Первого. Пусть 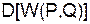есть дисперсия этой с.в. Естественно назвать среднее квадратическое отклонение с.в. 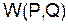, т.е. 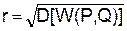риском для Первого при игре со стратегиями 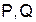. Поскольку выигрыш Первого есть проигрыш для Второго, то 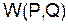есть случайный проигрыш Второго и r вполне естественно можно назвать риском игры с такими стратегиями и для Второго.

Предположим сначала, что игроки озабочены только максимизацией среднего дохода за партию игры – обычная цель в таких играх. Тогда игроки будут играть со своими оптимальными стратегиями: 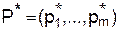– Первый игрок и 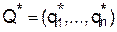– Второй.

Математическое ожидание с. в. 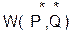называется ценой игры, обозначим ее .

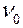Но что же можно назвать риском всей игры?

Вычислим дисперсию выигрыша Первого при оптимальных стратегиях игроков.

.

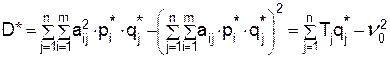Так как 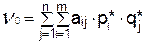, а через 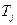обозначена сумма .

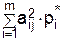Заметим, что в сумме 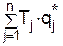можно оставить лишь те слагаемые, у которых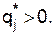

Заметим теперь, что если Первый играет со стратегией 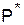, а Второй отвечает 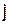-й чистой стратегией 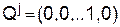, где единица находится на j-ом месте, то выигрыш первого есть с.в. с рядом распределения:

			…				…
			…				…

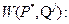
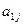
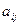
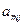
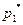
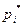
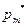
Если 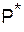есть оптимальная стратегия Первого, а 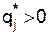, то из теории матричных игр с нулевой суммой известно, что выигрыш Первого при стратегиях Р* и 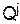по-прежнему равен цене игры 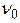, а дисперсия выигрыша Первого при этом равна 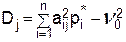, то есть равна 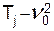. Таким образом, что происходит с риском выигрыша Первого, можно понять, сравнив дисперсию при оптимальных стратегиях и дисперсию 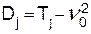или величины 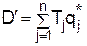и 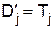. Пусть 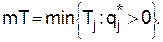Как легко понять, если среди 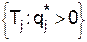есть разные числа, то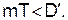

Теперь можно сделать следующий вывод:

Чуть-чуть отойдя от своей оптимальной стратегии (смотрите ниже Пример 1) и таким образом почти не уменьшив свой выигрыш, Первый может значительно уменьшить свой риск. При этом уменьшается и риск Второго, что отвечает и его интересам.

Чисто математически можно сказать, что в описанной ситуации риск выигрыша Первого не зависит от его стратегии непрерывно.

Рассмотрим подробно пример матричной игры с матрицей 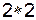. Как известно, общий случай в окрестности оптимальных стратегий игроков сводится к анализу такой игры.

Пример 1. Пусть матрица игры есть 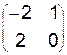. Графическое решение этой игры найдем, решив следующую задачу:

Z = →max; → max;

-2р₁ + 2р₂ ≥ , -4р₁ - ≥ -2,

р₁ ≥ , или подставляя вместо 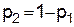, получаем: р₁ - ≥ 0,

р₁ + р₂ = 1, р₁ - ≥ 0,

р_1,2 ≥ 0, 0 ≤ р₁ ≤1.

Графическое решение последней задачи показано на следующем рисунке 1:

Оптимальным решением задачи будет т. А (2/5, 2/5). Поэтому цена игры ν₀ = 2/5 и P* = (2/5, 3/5). Стратегию Q* = (q₁*, q₂*) найдем, решив следующую СЛАУ:

-2 q₁* + q₂* = 2/5 Откуда: Q* = (1/5, 4/5)

2 q₁* = 2/5.

Отметим, что так как матрица игры не имеет седловой точки, то решение можно найти по следующим формулам:

= ,

= ,

= ,

= ,

= .

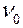
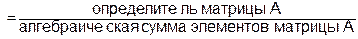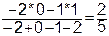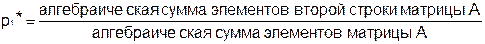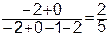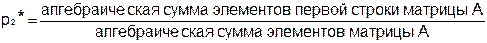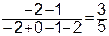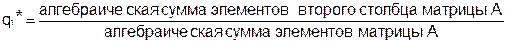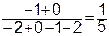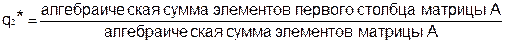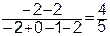Дисперсия выигрыша Первого при оптимальных стратегиях 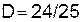, т. е. риск игры равен примерно 1. Далее вычисления дают 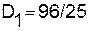, 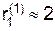; 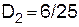, 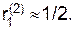Примерная, но достаточно точная зависимость риска Первого в малой окрестности его оптимальной стратегии показана на рис. 2.

Как видно из рис. 2 при отходе Первого от своей оптимальной стратегии вправо, т. е. при увеличении вероятности выбора им 1-й строки. Второй начинает отвечать 1-й чистой стратегией и риск Первого скачком увеличивается до 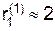, а при отходе Первого от своей оптимальной стратегии влево Второй переходит на свою 2-ю чистую стратегию и риск Первого скачком снижается до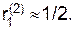

q₁

1/5

Рис. 3

Аналогичное верно и в отношении Второго. Кратко повторим. Примерная, но достаточно точная зависимость риска Второго в малой окрестности его оптимальной стратегии показана на рис. 3. Как видно из рис. 3, при отходе Второго от своей оптимальной стратегии вправо, т. е. при увеличении вероятности выбора им 1-й строки, Первый начинает отвечать 2-й чистой стратегией, и риск Второго скачком уменьшается до 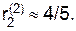, а при отходе Второго от своей оптимальной стратегии влево, Первый переходит на свою 1-ю чистую стратегию, и риск Второго скачком увеличивается до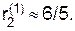

Пусть 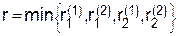. Эту величину и можно назвать риском всей игры. Однако играть с таким риском можно лишь при согласии обеих сторон. Для анализируемой игры 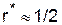и игроки для достижения такого риска должны играть так: Первый играет со своей оптимальной стратегией 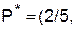3/5), а Второй должен использовать 2-ю чистую стратегию.

Пример 2. Рассмотрим пример игры с платежной матрицей размера 4x5:

		-3			-5
A4,5=(аij)4,5 =	-3		-3	-5
	-5	-3	-5		-6
		-5			-7

Вначале проведет анализ на доминирование. i-я строка доминирует j-ю, если все элементы i-й строки больше или равны соответствующих элементов j-й. Так как строки выбирает Первый игрок, то мы исключаем из платежной матрицы доминируемые строки. В нашем примере 1-я строка доминирует 3-ю. В результате исключения 3-й строки получим

		-3			-5
A`3,5=(аij)3,5 =	-3		-3	-5
		-5			-7

Третий столбик доминирует первый и, так как столбцы выбирает Второй игрок, то мы исключаем доминирующий третий столбец. В результате получим платежную матрицу 3´4, которую упростить уже невозможно.

					ai
		-3		-5	-5
A``3,4 =	-3		-5		-5
				-7	-7
bj

Далее приведем анализ игры на седловую точку. Находим минимумы по строкам a_i. Тогда нижняя цена игры

a= -5.

Найдем максимумы по столбцам b_j. Тогда верхняя цена игры

b=4.

Поскольку a¹b, то решения игры в чистых стратегиях нет. Будем искать решение в смешанных стратегиях. Предварительно прибавим к каждому элементу платежной матрицы константу, равную 7, сделав их неотрицательными. Решение игры при этом не изменится, а цена игры возрастет на 7 и будет больше нуля.

Матрица игры примет следующий вид:

		9
	A’’3,4+7=

В силу теоремы Неймана решение игры сводится к нахождению решений симметричной пары взаимно двойственных задач линейного программирования. Пусть P=(p₁;p₂;p₃); Q=(q₁;q₂;q₃;q₄)- стратегии игроков. Найдем сначала Q*

Если Второй игрок применяет свою оптимальную стратегию, то Первый игрок не может улучшить свое положение, отступая от своей оптимальной стратегии. Заставим Первого игрока отступать от своей оптимальной стратегии, пользуясь чистыми стратегиямиp₁, p_2, p₃ (а Второй игрок, между тем, придерживается своей оптимальной стратегии Q*). В любом случае проигрыш Второго игрока будет не больше, чем цена игры

9q₁ + 4q₂ + 11q₃ + 2q₄ £ ,

4q₁ + 11q₂ + 2q₃ + 13q₄ £ ,

11q₁ + 2q₂ + 13q₃ £ .

Разделим каждое из неравенств на > 0 и введем обозначения

qj
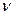
	= xj ³0 (j=1,4).

Получим

9x₁ + 4x₂ + 11x₃ + 2x₄ £ 1,

4x₁ + 11x₂ + 2x₃ + 13x₄ £ 1,

11x₁ + 2x₂ + 13x₃ £ 1.

Поскольку å q_j=1, то переменные x₁,x₂,x₃,x₄ удовлетворяют условию

j=1

x₁ + x₂ + x₃ + x₄ = .

Но есть проигрыш второго игрока, который он стремится сделать минимальным. Следовательно, величина 1/ должна быть максимальна. Таким образом, имеем следующую задачу линейного программирования.

Найти вектор x=(x₁,x₂,x₃,x₄), который обеспечивает максимум целевой функции

Z =x₁+x₂+x₃+x₄®max,

при следующих линейных ограничениях:

9x₁ + 4x₂ + 11x₃ + 2x₄ £ 1,

4x₁ + 11x₂ + 2x₃ + 13x₄ £ 1, (1)

11x₁ + 2x₂ + 13x₃ £ 1,

x₁,x₂,x₃,x₄ ³0.

После приведенной задачи к основной задаче линейного программирования найдем ее оптимальное решение симплексным методом:

X*=(0; 1/28; 1/14; 1/28), при значении целевой функции Z_max=1/7.

Цену игры и Q* найдем по следующей формуле:

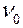= 1/Z _max = 7; Q* = 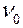*X* = (0, ¼, ½, ¼).

В качестве проверки, студент может решить эту задачу с использованием компьютера (см. приложение 12).

Найдем теперь оптимальную стратегию P* первого игрока. Если Первый игрок применяет свою оптимальную стратегию, то Второй игрок не может улучшить свое положение, отступая от своей оптимальной стратегии. В случае использования Вторым игроком своих чистых стратегий, а Первым игроком своей оптимальной стратегии, выигрыш Первого будет не меньше, чем цена игры:

9p₁ + 4p₂ + 11p₃ ³ ,

4p₁ + 11p₂ + 2p₃ ³ ,

11p₁ + 2p₂ + 13p₃ ³ ,

2p₁ + 13p₂ ³ .

Разделим каждое из неравенств на > 0 и введем обозначения:

p_i

=y_i ³ 0 (i=1,3).

Получим:

9y₁ + 4y₂ + 11y₃ ³ 1,

4y₁ + 11y₂ + 2y₃ ³ 1,

11y₁ + 2y₂ + 13y₃ ³ 1,

2y₁ + 13y₂ ³ 1.

Поскольку å p_i=1, то переменные y₁,y₂ ,y₃ удовлетворяют условию

i=1

y₁+y₂ +y₃ = 1/ .

Но есть выигрыш Первого игрока, который стремится его максимизировать. Следовательно, величина 1/ должна быть минимальна. Таким образом имеем следующую задачу линейного программирования.

Найти вектор y=(y₁,y₂ ,y₃), который обеспечивает минимум целевой функции:

L= y₁+y₂ +y₃®min.

При следующих линейных ограничениях:

9y₁ + 4y₂ + 11y₃ ³ 1,

4y₁+ 11y₂ + 2y₃ ³ 1, (2)

11y₁ + 2y₂ + 13y₃ ³ 1,

2y₁ +13y₂ ³ 1,

y₁,y₂ ,y₃³ 0.

Эта задача является двойственной по отношению к рассмотренной выше задаче (1). Решение задачи (2) возьмем из последней симплексной таблицы при решении задачи (1):

Уопт = (1/28, 1/14 1/28); Lmin = Zmax = 1/7.

Откуда цена игры u₀ по-прежнему равна 7.

Далее, найдем P* = ₀*y_опт = (1/4, 1/2, 1/4).

Отметим, что решение задачи (2) можно также найти с помощью второй основной теоремы двойственности.

Возвращаемся теперь к исходной матрице игры A_4,5 . Решение этой игры имеет вид:

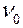=0; P* = (1/4, 1/2, 0, 1/4); Q* = (0, 1/4, 0, 1/2, 1/4,).

Найдем риск игры при использовании игроками своих оптимальных стратегий

r₀ = 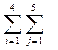а_ij² p_i* q_j* - 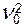= √ 26,

а также риск при использовании одним из игроков своей чистой, а другим – своей оптимальной стратегии (нижний индекс Первого игрока, верхний – Второго игрока):

D_(p*) ^(Q2)= å a_i2² p_i* - 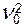=(-3)²´1/4 + 4²´1/2+(-5)²´1/4- 0² = 33/2; r₍₀₎⁽²⁾ = √33/2,

i=1

D_(p*) ^(Q4)= å a_i3² p_i* - 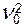= (4)²´1/4 + (-5)²´1/2+6²´1/4- 0² = 51/2; r₍₀₎⁽²⁾ = √51/2,

i=1

D_(p*) ^(Q5)= å a_i4² p_i* - 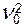= (-5)²´1/4 + 6²´1/2+(-7)²´1/4- 0² = 73/2; r₍₀₎⁽⁴⁾= √73/2,

i=1

D_(p1) ^(Q*)= åa_1j² q_j*- 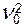= 2²´0+(-3)²´1/4+4²´1/2+(-5)²´1/4- 0²=33/2; r₍₁₎⁽⁰⁾=√33/2,

j=1

D_(p2) ^(Q*)= åa_2j² q_j*- 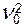=(-3)²´0+4²´1/4+(-5)²´1/2+6²´1/4- 0²=51/2; r₍₂₎⁽⁰⁾= √51/2,

j=1

D_(p4) ^(Q*)= åa_3j² q_j*- 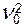=4²´0+(-5)²´1/4+6²´1/2+(-7)²´1/4- 0²=73/2; r₍₃₎⁽⁰⁾= √73/2.

j=1

Минимальное значение риска равно √33/2, и меньше r₀. Этот риск соответствует ситуациям, когда Первый игрок играет по оптимальной стратегии, а Второй игрок использует вторую чистую стратегию Q₂; или, когда Первый игрок использует свою первую чистую стратегию P₁, а Второй игрок – оптимальную Q*. Однако играть с таким риском, как отмечалось выше, можно только с согласия обеих игроков, то есть при их сотрудничестве друг с другом.

Дата добавления: 2015-06-04