Решение задачи линейного программирования с помощью средств Поиск решения MS Excel

Рассмотрим основные этапы процесса решения задачи линейного программирования с помощью Excel на примере задачи об оптимальном плане выпуска продукции (условие задачи представлено в примере 1).

Этап 1. Организуйте данные на листе MS Excel так, как это показано на рисунке 1.

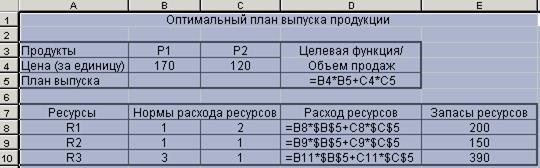
Рисунок 1. Постановка задачи нахождения оптимального плана выпуска продукции.

· В ячейках В5 и С5 будут расположены искомые значения переменных Х₁ и Х_2.

· В ячейку D5 введена формула, которая позволяет вычислять значение целевой функции Z=170*X₁+120*X₂ (представляющей общий объем реализованной продукции) при продаже X₁ изделий первого вида и X₂ изделий второго вида.

· В ячейки D8, D9, D10 - введены формулы, отражающие общий расход ресурсов R₁, R₂, R₃ при выпуске X₁ изделий первого вида и X₂ - изделий второго вида.

R₁ 1* Х₁ + 2* Х₂

R₂ 1* Х₁ + 1* Х₂

R₃ 3* Х₁ + 1* Х₂

Этап 2. Выберите пункт меню Сервис – Поиск Решения. Появится окно Поиск решения (Рисунок 2).

· В поле окна “Установить целевую ячейку” отметьте ячейку D5 (щелкните сначала по полю окна, а затем по ячейке D5)

· Установите флажок на отметке “Равной максимальному значению”

· В поле окна “Изменяя ячейки” отметьте ячейки В5 и С5

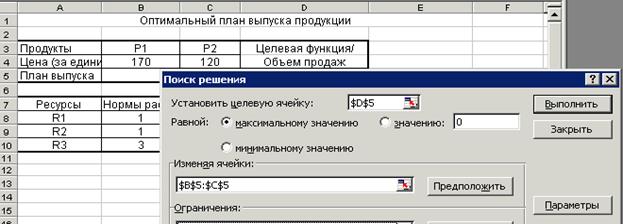
Рисунок 2. Задание целевой ячейки и изменяемых ячеек.

Этап 3. Введите последовательно все ограничения, щелкая по кнопке “Добавить” (как показано на рисунках 3 и 4)

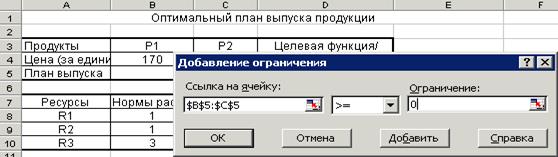
Рисунок 3. Введение условий неотрицательности переменных.

· В появившемся окне щелкните в поле “Ссылка на ячейку”, а затем отметьте ячейки B5:C5, выберите знак ограничения ³, щелкните на правое поле “Ограничение” и введите в него значение 0. Таким образом Вы ввели ограничения: X₁,X₂ ³0.

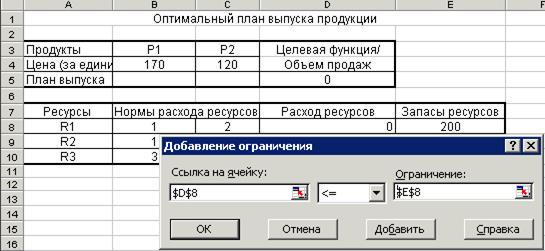
Рисунок 4. Введение ограничений по объемам ресурсов.

· Вновь щелкните на кнопке “Добавить”. В появившемся окне щелкните в поле “Ссылка на ячейку”, а затем отметьте ячейку D8, выберите знак ограничения £, щелкните на правое поле “Ограничение” и отметьте в нем ячейку E8, содержащую ограничение на доступный объем ресурса R ₁. Таким образом, Вы ввели ограничение 1*X₁+2*X₂ £ 200.

· Продолжайте процесс и введите ограничения по объемам ресурсов R₂, R₃.

Этап 4. Нахождение оптимального решения.

После того, как введены все ограничения, следует щелкнуть на кнопке «Параметры» и в открывшемся окне установить флажок «Линейная модель», для получения решения достаточно щелкнуть на кнопке “Выполнить” Полученное решение представлено на рисунке 5.

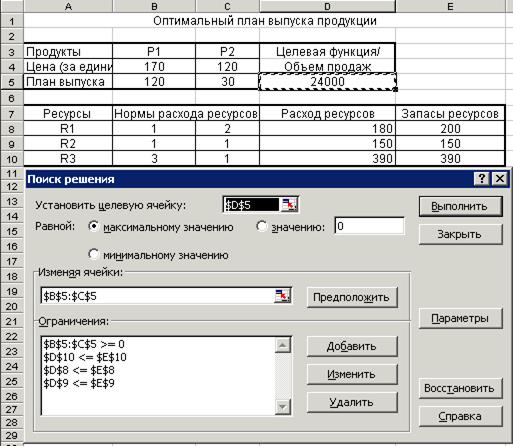
Рисунок 5. Оптимальный план выпуска.

В ячейке D5 приведено оптимальное значение целевой функции. При соблюдении всех ограничений максимальный объем продаж может составить 24000. Оптимальные объемы выпуска изделий первого и второго вида указаны в ячейках B5:C5:X₁ =120, X₂ = 30.

В ячейках D8, D9, D10 содержатся объемы ресурсов, которые будут необходимы для реализации найденного оптимального плана. При этом можно заметить, что ресурсы второго и третьего вида будут израсходованы полностью, а для ресурса первого вида останется неиспользованный запас (избыток) в 20 единиц.

Анализ оптимального решения в задачах линейного программирования.

При построении формальной модели по условиям примерамы поставили цель – найти такие объемы выпуска продукции (значения переменных Х1 и Х2), при которых общая выручка от продажи достигнет максимально возможного значения при соблюдении ограничений по ресурсам. В полученном решении, представленном на рисунке 5., содержится информация об оптимальных значениях переменных Х1= 120, Х2 = 30 и максимальном объеме продаж Z = 24000. Но в этом решении содержится также полезная дополнительная информация – сведения о фактическом расходовании ресурсов при реализации оптимального плана. Из рисунка 5 видно, что в соответствии с оптимальным планом второй и третий ресурсы будут использованы полностью, а для ресурса первого вида имеется остаток (резерв) в размере 20 единиц.

Для увеличения объема продаж руководство предприятия может рассматривать разные варианты действий. Среди них наиболее простыми следует признать два направления: приобретение дополнительных ресурсов у поставщиков (и увеличение за счет этого объемов выпуска); увеличение цен на некоторые изделия компании. При этом вопросы можно конкретизировать следующим образом: как изменятся значения переменных и значение целевой функции при изменении объема ресурса определенного вида. Какое влияние на значения переменных и значение целевой функции могут оказать изменения цен на определенные изделия. Теоретической основой для проведения такого рода пост оптимизационного анализа полученных решений является теория двойственных задач линейного программирования. Поскольку подобные варианты решений достаточно распространены, то соответствующие инструменты включены в набор стандартных средств решения задач линейного программирования. После того, как введены все ограничения и нажата кнопка “Выполнить”, будет получено оптимальное решение и предложено несколько типов отчетов (рисунок 6). Отчеты размешаются на отдельных листах Рабочей книги.

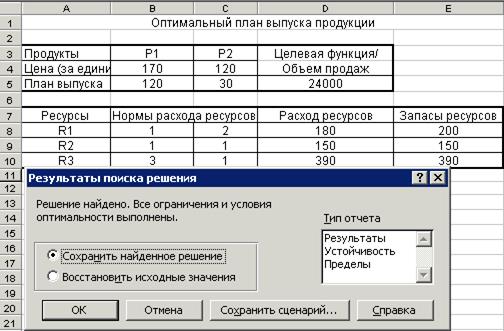
Рисунок 6. Выбор типа отчета для пост оптимизационного анализа.

Рассмотрим дополнительную информацию, которую может получить менеджер из Отчета по устойчивости, представленного на рисунке 7.

Например, из первой строки мы можем увидеть, что оптимальный план выпуска будет оставаться неизменным при изменении цены на продукт Р1 в диапазоне от 120 (начальная цена 170 минус допустимое снижение на 50) до 360 (начальная цена 170 плюс допустимое повышение на 190). Конечно, при этом оптимальное значение целевой функции будет изменяться. Аналогичным образом можно интерпретировать информацию о пределах изменения цены на продукт Р2.

По отношению к возможным изменениям объемов ресурсов представленная в Отчете по устойчивости информация имеет иной смысл. Например, в последней строке Отчета по устойчивости, представленного на рисунке 7, содержится информация о том, что в соответствии с оптимальным планом фактический расход ресурса третьего вида равен 390 и совпадает с допустимым объемом ресурса данного вида. Если доступный для выпуска продукции объем третьего ресурса будет изменяться в диапазоне от 350 (плановый объем 390 минус допустимое уменьшение на 40) до 450 (плановый объем 390 плюс допустимое увеличение на 60), то структура оптимального плана останется неизменной. Это означает, что будут выпускаться оба вида изделий, дефицитными будут оставаться второй и третий ресурсы, а первый ресурс будет избыточным. При этом теневая цена показывает, что увеличение допустимого объема третьего ресурса на одну единицу приведет к росту целевой функции на 25.

Поскольку ресурс первого вида является избыточным для реализации найденного оптимального плана, то, во-первых, любое увеличение объема этого ресурса никак не скажется на оптимальных объемах выпуска продукции, а теневая цена равная 0 показывает, что увеличение объема первого ресурса или снижение допустимого объема (не более чем на 20 единиц) никак не повлияют и на значение целевой функции.

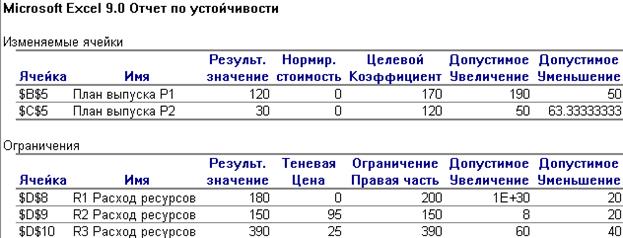
Рисунок 7. Отчет по устойчивости для оптимального решения Примера 1.

Пример 2. Рассмотрим пример решения задачи линейного программирования из задания на курсовую работу (3 ресурса и 4 продукта). На рисунках 8 и 9 показаны формы представления исходных данных, результаты решения задачи и отчет об устойчивости.

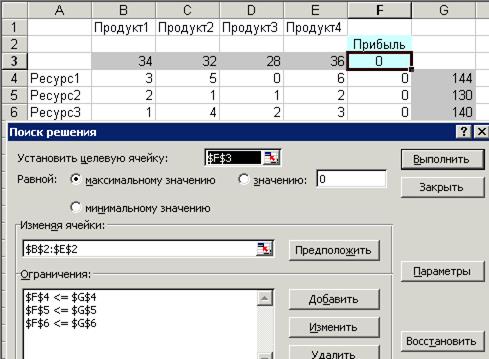
Рисунок 8. Исходные данные для примера 2.

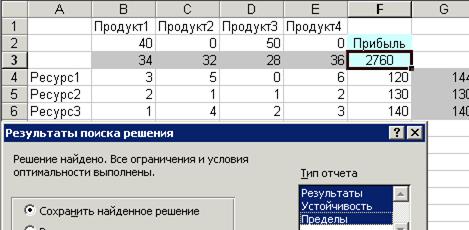
Рисунок 9. Основные результаты для примера 2.

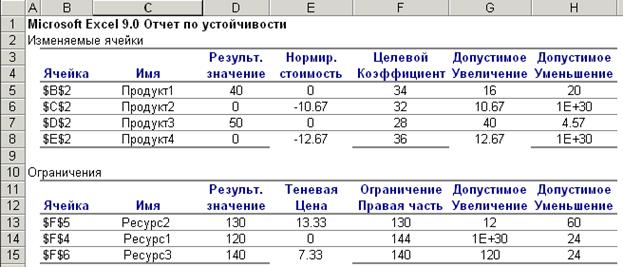
Рисунок 10. Анализ устойчивости оптимального решения для примера 2.

Дата добавления: 2015-06-04