
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Подсчет параметров и оценка типа распределения
|
|
|
|
Для описания выборочного распределения, как правило, используются следующие известные параметры [1, 11, 15]:
1. Среднее арифметическое:
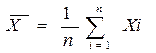 ; где:
; где:
Xi; - балл i-того испытуемого;
n - количество испытуемых в выборке (объем);
Выборочная, или средняя, квадратическая ошибка средней арифметической:
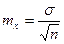 .
.
2. Среднее квадратическое (стандартное) отклонение:
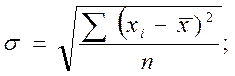
Σ - сумма квадратов тестовых баллов для n испытуемых.
Средняя ошибка среднего квадратического (стандартного) отклонения:
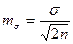 .
.
Стандартная ошибка среднего арифметического (математического ожидания) оценивается по формуле: 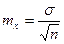 на основе ошибки математического ожидания строятся доверительные границы, в которых заключена величина генеральной средней:
на основе ошибки математического ожидания строятся доверительные границы, в которых заключена величина генеральной средней: 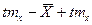 .
.
Если тестовый балл какого-либо испытуемого попадает в границы доверительного интервала, то нельзя считать, что испытуемый обладает повышенным (или пониженным) значением измеряемого свойства с заданным уровнем статистической вероятности.
Оценка достоверности вычисленных статистик производится по следующим формулам:
Критерий достоверности различий, наблюдаемых между средними арифметическими двух независимых выборок:
 .
.
3. Асимметрия:
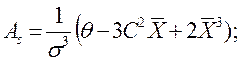
где: Х - среднее арифметическое;
σ - стандартное отклонение;
θ - среднее кубическое: 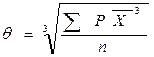 ;
;
С - среднее квадратическое: 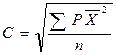 ;
;
Р - частота появления варианты.
Коэффициент асимметрии величина не именованная. Он колеблется в пределах от нуля до единицы. При совершенно симметричных распределениях коэффициент асимметрии равен нулю. Асимметрия считается незначительной, если 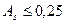 . При
. При 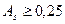 скошенность распределения оказывается уже значительной.
скошенность распределения оказывается уже значительной.
4. Эксцесс: 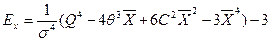 ,
,
Q - среднее значение четвертой степени: 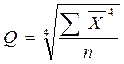
При положительном эксцессе показатель 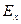 - число положительное, а при отрицательном -
- число положительное, а при отрицательном - 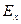 - число отрицательное. Если
- число отрицательное. Если 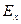 ≤ 0,2, эксцесс практически отсутствует; если же
≤ 0,2, эксцесс практически отсутствует; если же 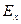 ≥0,5, но ≤ 1, эксцесс считается заметным, но небольшим. Предельное значение отрицательного
≥0,5, но ≤ 1, эксцесс считается заметным, но небольшим. Предельное значение отрицательного 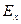 равно - 2, что указывает на наличие распределения с двумя вершинами.
равно - 2, что указывает на наличие распределения с двумя вершинами.
Асимметрия и эксцесс нормального распределения должны быть равны нулю. Если они существенно отклоняются от нуля (хотя бы один из двух параметров), то это означает, что полученное эмпирическое распределение анормально.
Проверку значимости асимметрии можно произвести на основе общего неравенства Чебышева:
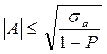 ; ("а")
; ("а")
где:
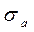 - дисперсия эмпирической оценки асимметрии:
- дисперсия эмпирической оценки асимметрии:
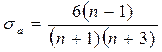 , где
, где
р - уровень значимости или вероятность ошибки первого рода; ошибки в том, что будет принят вывод о незначимости асимметрии, при наличии значимой асимметрии (в формулу подставляют стандартные р= 0,05 или р= 0,01 и проверяют выполнение неравенства).
Сходным образом оценивается значимость эксцесса:
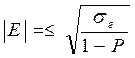 , ("б")
, ("б")
где:
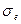 -эмпирическая дисперсия оценки эксцесса, определяется по формуле:
-эмпирическая дисперсия оценки эксцесса, определяется по формуле:
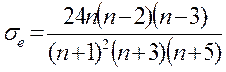
Гипотезы об отсутствии асимметрии и эксцесса принимаются с вероятностью ошибки р (пренебрежимо малой), если выполняются неравенства ("а") и ("б").
Если проверка согласованности эмпирического распределения с нормальным дает положительные результаты, то это означает, что полученное распределение можно рассматривать как устойчивое - репрезентативное по отношению к генеральной совокупности - а, значит, на его основе можно определить репрезентативные тестовые нормы. Если проверка не выявляет нормальности на заданном уровне, то это означает, что или выборка мала и нерепрезентативна к популяции, или измеряемое свойство и устройство теста (способ подсчета) вообще не дают нормального распределения [15].
В принципе, требование нормальности распределения не является обязательным. Можно с равным успехом пользоваться другими хорошо разработанными моделями гамма-распределения, пуассоновского распределения и т.п. Критерий Колмогорова позволяет оценить близость эмпирического распределения к любому теоретическому распределению. При этом устойчивым и репрезентативным может оказаться распределение любого типа. Если из нормальности, как правило, следует устойчивость, то обратное неверно - устойчивость вовсе не обязательно предполагает нормальность распределения.
Наличие значимой положительной асимметрии свидетельствует о том, что в системе факторов, детерминирующих значение измеряемого показателя, преобладают факторы, действующие в одном направлении - в сторону повышения показателя.
На практике распределения такого рода преобразуют в нормальное (приближенно нормальное) с помощью логарифмической трансформации: Z = Ln y. При этом говорят, что распределение показателей подчиняется "логнормальному" закону.
Подобную алгебраическую нормализацию тестовой шкалы применяют к показателям с еще более резко выраженной положительной асимметрией.
Например, в процедурах контент-анализа сам тестовый показатель является частотным - он измеряет частоту появления определенных категорий событий в текстах.
Приложение 2.
Статистические таблицы значимости*
Таблица 1. Значимость Т-распределения Стьюдента.
| Число степеней свободы | Уровень значимости | |||||
| 0,10 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| 6,314 | 12,71 | 31,82 | 63,66 | 318,3 | 636,6 | |
| 2,920 | 4,303 | 6,965 | 9,925 | 22,33 | 31,60 | |
| 2,353 | 3,182 | 4,541 | 5,841 | 10,21 | 12,92 | |
| 2,132 | 2,776 | 3,747 | 4,604 | 7,173 | 8,610 | |
| ' | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 | 6,869 |
| 1,943 | 2,447 | 3,143 | 3,707 | 5,208 | 5,959 | |
| 1,895 | 2,365 | 2,998 | 3,499 | 4,785 | 5,408 | |
| 1,860 | 2,306 | 2,896 | 3,355 | 4,501 | 5,041 | |
| 1,833 | 2,262 | 2,821 | 3,250 | 4,297 | 4,781 | |
| 1,812 | 2,228 | 2,764 | 3,169 | 4,144 | 4,587 | |
| 1,796 | 2,201 | 2,718 | 3,106 | 4,025 | 4,437 | |
| 1,782 | 2,179 | 2,681 | 3,055 | 3,930 | 4,318 | |
| 1,771 | 2,160 | 2,650 | 3,012 | 3,852 | 4,221 | |
| 1,761 | 2,145 | 2,624 | 2,977 | 3,787 | 4,140 | |
| 1,753 | 2,131 | 2,602 | 2,947 | 3,733 | 4,073 | |
| 1,746 | 2,120 | 2,583 | 2,921 | 3,686 | 4,015 | |
| 1,740 | 2,110 | 2,567 | 2,898 | 3,646 | 3,965 | |
| 1,734 | 2,101 | 2,552 | 2,878 | 3,610 | 3,922 | |
| 1,729 | 2,093 | 2,539 | 2,861 | 3,579 | 3,883 | |
| 1,725 | 2,086 | 2,528 | 2,845 | 3,552 | 3,850 | |
| 1,721 | 2,080 | 2,518 | 2,831 | 3,527 | 3,819 | |
| 1,717 | 2.074 | 2,508 | 2,819 | 3,505 | 3,792 | |
| 1,714 | 2,069 | 2,500 | 2,807 | 3,485 | 3,767 | |
| 1,711 | 2,064 | 2,492 | 2,797 | 3,467 | 3,745 | |
| 1,708 | 2,060 | 2,485 | 2,787 | 3,450 | 3,725 | |
| 1,706 | 2,056 | 2,479 | 2,779 | 3,435 | 3,707 | |
| 1,703 | 2,052 | 2,473 | 2,771 | 3,421 | 3,690 | |
| 1,701 | 2,048 | 2,467 | 2,763 | 3,408 | 3,674 | |
| 1,699 | 2,045 | 2,462 | 2,756 | 3,396 | 3,659 | |
| 1,697 | 2,042 | 2,457 | 2,750 | 3,385 | 3,646 | |
| ∞ | 1,645 | 1,960 | 2,326 | 2,576 | 3,090 | 3,291 |
Таблица дает значения введенной Стьюдентом величины t для уровней значимости, наиболее часто применяющихся при нахождении критериев значимости и границ доверительного интервала.
Приложение 2.
Таблица 2. Критические значениякритерия χ2 для трех степеней доверительной вероятности
| р n | 0,95 | 0,99 | 0,999 | Р n | 0.95 | 0,99 | 0,999 |
| 3,8 | 6,6 | 10,8 | 38,9 | 45,6 | 54,1 | ||
| 6,0 | 9,2 | 13,8 | 40,1 | 47,0 | 55,5 | ||
| 7,8 | 11,3 | 16,3 | 41,3 | 48,3 | 56,9 | ||
| 9,5 | 13,3 | 18,5 | 42,6 | 49,6 | 58,3 | ||
| 11,1 | 15,1 | 20,5 | 43,8 | 50,9 | 59,7 | ||
| 12,6 | 16,8 | 22,5 | 46,2 | 53,5 | 62,4 | ||
| 14,1 | 18,5 | 24,3 | 48,6 | 56,0 | 65,2 | ||
| 15,5 | 20,1 | 26,1 | 51,0 | 58,6 | 67,9 | ||
| 16,9 | 21,7 | 27,9 | 53,4 | 61,1 | 70,7 | ||
| 18,3 | 23,2 | 29,6 | 55,8 | 63,7 | 73,4 | ||
| 19,7 | 24,7 | 31,3 | 58,1 | 66,2 | 76,1 | ||
| 21,0 | 26,2 | 32,9 | 60,5 | 68,7 | 78,7 | ||
| 22,4 | 27,7 | 34,5 | 62,8 | 71,2 | 81,4 | ||
| 23,7 | 29,1 | 36,1 | 65,2 | 73,7 | 84,0 | ||
| 25,0 | 30,6 | 37,7 | 67,5 | 76,2 | 86,7 | ||
| 26,3 | 32,0 | 39,3 | 73,3 | 82,3 | 93,2 | ||
| 27,6 | 33,4 | 40,8 | 79,1 | 88,4 | 99,6 | ||
| 28,9 | 34,8 | 42,3 | 89,8 | 94,4 | 106,0 | ||
| 30,1 | 36,2 | 43,8 | 90,5 | 100,4 | 112,3 | ||
| 31,4 | 37,6 | 45,3 | 96,2 | 106,4 | 118,5 | ||
| 32,7 | 38,9 | 46,8 | 101,9 | 112,3 | 124,8 | ||
| 33,9 | 40,3 | 48,3 | 107,5 | 118,2 | 131,0 | ||
| 35,2 | 41,6 | 49,7 | 113,1 | 124,1 | 137,1 | ||
| 36,4 | 43,0 | 51,2 | 118,7 | 130,0 | 143,3 | ||
| 37,7 | 44,3 | 52,6 | 124,3 | 135,8 | 149,4 |
Приложение 2.
Таблица 3. Значимость коэффициента корреляции (по Пирсону)
| Число степеней свободы (n) | Уровень значимости | ||||||||||||||||
| 0,10 | 0,05 | 0,02 | 0,01 | 0, 001 | |||||||||||||
| 0,9877 Э877 | 0,99692 | 0,99951 | 0,99988 | 0,9999988 | |||||||||||||
| 0,9000 | 0,9500 | 0,9800 | 0,9900 | 0,9990 | |||||||||||||
| 0,805 | 0,878 | 0,9343 t3 | 0,9587 | 0,9911 | |||||||||||||
| 0,7 29 | 0,811 | 0,882 | 0,9172 | 0,9741 | |||||||||||||
| 0,669 | 0,754 | 0,833 | 0,875 | 0,9509 | |||||||||||||
| 0,621 | 0,707 | 0,789 | 0,834 | 0,9249 | |||||||||||||
| 0,582 | 0,666 | 0,750 | 0,798 | 0,898 | |||||||||||||
| 0,549 | 0,632 | 0,715 | 0,765 | 0,872 | |||||||||||||
| 0,521 | 0,602 | 0,685 | 0,735 | 0,84 7 | |||||||||||||
| 0,497 | 0,576 | 0,658 | 0,708 | 0,82 3 | |||||||||||||
| 0,476 | 0,553 | 0,634 | 0,684 | 0,801 | |||||||||||||
| 0,457 | 0,532 | 0,612 | 0,661 | 0,780 | |||||||||||||
| 0,441 | 0,514 | 0,592 | 0,641 | 0,760 | |||||||||||||
| 0,426 | 0,497 | 0,574 | 0,623 | 0,742 | |||||||||||||
| 0,412 | 0,482 | 0,558 | 0,606 | 0.725 | |||||||||||||
| 0,400 | 0,468 | 0,543 | 0,590 | 0,708 | |||||||||||||
| 0,389 | 0,456 | 0,529 | 0,575 | 0,693 | |||||||||||||
| 0,378 | 0,444 | 0,516 | 0,561 | 0,679 | |||||||||||||
| 0,369 | 0,433 | 0,503 | 0,549 | 0,665 | |||||||||||||
| 0,360 | 0,423 | 0,492 | 0,537 | 0,652 | |||||||||||||
| 0.323 | 0,381 | 0,445 | 0,487 | 0,597 | |||||||||||||
| 0,296 | 0,349 | 0,409 | 0,449 | 0,554 | |||||||||||||
| 0,275 | 0,325 | 0,381 | 0,418 | 0,519 | |||||||||||||
| 0,257 | 0,304 | 0,358 | 0,393 | 0,490 | |||||||||||||
| 0,243 | 0,288 | 0,338 | 0,372 | 0,465 | |||||||||||||
| 0,231 | 0,273 | 0,322 | 0,354 | 0,443 | |||||||||||||
| 0,211 | 0,250 | 0,295 | 0,325 | 0,408 | |||||||||||||
| 0,195 | 0,232 | 0,274 | 0,302 | 0,380 | |||||||||||||
| 0,183 | 0,217 | 0,257 | 0,283 | 0,357 | |||||||||||||
| 0,173 | 0,205 | 0,242 | 0,267 | 0,338 | |||||||||||||
| 0,164 | 0,195 | 0,230 | 0,254 | 0,321 | |||||||||||||
Приложение 2.
Таблица 4. Значимость коэффициента корреляции рангов (по Спирмену).
| n | 0,05 | 0,01 | n | 0,05 | 0,01 | n | 0,05 | 0.01 |
| 0,94 | - | 0,48 | 0,62 | 0,37 | 0,48 | |||
| 0,85 | - | 0,47 | 0,60 | 0,36 | 0,47 | |||
| 0,78 | 0,94 | 0,46 | 0,58 | 0,36 | 0,46 | |||
| 0,72 | 0,88 | 0,45 | 0,57 | 0,36 | 0,45 | |||
| 0,68 | 0,83 | 0,44 | 0,56 | 0,34 | 0,45 | |||
| 0,64 | 0,79 | 0,42 | 0,54 | 0,34 | 0,44 | |||
| 0,61 | 0,76 | 0,42 | 0,53 | 0,33 | 0,43 | |||
| 0,58 | 0,73 | 0,41 | 0,52 | 0,33 | 0,43 | |||
| 0,56 | 0,70 | 0,40 | 0,51 | 0,33 | 0,42 | |||
| 0,54 | 0,68 | 0,39 | 0,50 | 0,32 | 0,41 | |||
| 0,52 | 0,66 | 0,38 | 0,49 | 0,32 | 0,41 | |||
| 0,50 | 0,64 | 0,38 | 0,48 | 0,31 | 0,40 |
Примечание*. Таблицы приложения 2 взяты из книг [11, 18]:
- Лакин Г.Ф. Биометрия. М.: Высшая школа, 1968. - 284 с.
- Психологическая диагностика: Учебное пособие / Под ред. К.М. Гуревича и Е.М. Борисовой. - М.: Изд-во УРАО, 1997. - 304 с.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 891; Нарушение авторских прав?; Мы поможем в написании вашей работы!