Доставка до курьерской и транспортной компании бесплатна

Закон ампера Вектор совпадает по направлению с током. Данная формула выражает закон Ампера: сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника и магнитной индукции поля

Способ нанесения изображений, узоров и текстур с помощью Фотопечати.

Витраж и др.

Тампонная печать.

Перенос изображений резиновыми штампами.

. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля. Лаплас обобщил экспериментальные результаты Био и Савара в виде дифференциального закона, называемого законом Био – Савара – Лапласа, по которому магнитная индукция 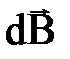, создаваемая в некоторой точке А элементом проводника dℓ с током I,

Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле

. Сила действующая на электрический заряд, движущийся в магнитном по скоростью. Сила Лоренца

циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:

11) Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.

. Потоком вектора магнитной индукции через элементарную площадку dS называется физическая величина dФ_m, равная произведению величины этой площадки и проекции вектора В на направление нормали к площадке dS

Поскольку каждый интеграл по отдельности равен нулю, то и

вышеизложенное составляет суть теоремы Гаусса для потока магнитного поля Ф_m. Поток магнитного поля через любую замкнутую поверхность равен нулю. Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

. Намагниченность вещества. Ранее мы предполагали, что провода, несущие ток и создающие магнитное поле, находятся в вакууме. Если же провода находятся в какой-либо среде, то величина создаваемого ими магнитного поля изменится. Это объясняется тем, что всякое вещество, всякая среда способна под действием магнитного поля приобретать магнитный момент, т.е. намагничиваться. Поэтому каждое вещество является магнетиком. Благодаря орбитальным магнитным моментам электронов в атомах, вещество создает свое собственное магнитное поле, которое накладывается на внешнее поле 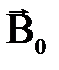. Согласно принципу суперпозиции полей оба поля в сумме дают результирующее поле:

Это усредненное (макроскопическое) поле, действующее в веществе.

Если внешнее поле отсутствует (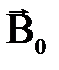 = 0), то молекулярные токи чаще всего ориентированы беспорядочным образом, ориентация магнитных моментов отдельных молекул хаотична, и поэтому создаваемое ими собственное поле 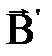также равно нулю. Под действием внешнего поля ( 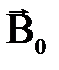≠ 0) магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего суммарный магнитный момент 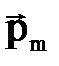уже не равен нулю, и магнетик намагничивается, возникает поле 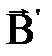. Количественной характеристикой намагниченного состояния вещества служит векторная величина - намагниченность J, равная отношению магнитного момента некоторого малого объема вещества к этому объему. Другими словами, намагниченность - это магнитный момент единицы объема вещества:

Гиромагнитное отношение – отношение дипольного магнитного момента элементарной частицы (или системы элементарных частиц) к ее механическому моменту

12)Диамагнетизм. Диамагнетики. К диамагнетикам относятся такие вещества, у которых магнитный момент атома или молекулы в отсутствие внешнего магнитного поля равен нулю:

Магнитные моменты электронов в таких атомах в отсутствие внешнего магнитного поля взаимно скомпенсированы. Это характерно для атомов и молекул с полностью заполненными электронными оболочками, например для атомов инертных газов, молекул водорода, азота. При внесении такого вещества в магнитное поле его атомы и молекулы, согласно теореме Лармора, приобретают наведенные магнитные моменты 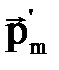, направленные для всех атомов и молекул одинаково против поляДля диамагнитных веществ существует линейная зависимость намагниченности от величины напряженности внешнего поля:

Итак, диамагнитные вещества намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции. Это свойство называется диамагнетизмом (диамагнитным эффектом). Характерно то, что диамагнетизм не зависит от температуры.

Парамагнетизм. Парамагнетики. К парамагнетикам относятся вещества, у которых магнитный моментатомов или молекул отличен от нуля в отсутствие внешнего магнитного поля: …….

Поэтому парамагнетики при внесении их во внешнее магнитное поле намагничиваются в направлении поля. В отсутствие внешнего магнитного поля парамагнетик не намагничен, так как из-за теплового движения все магнитные моменты

Рис.2.7. Парамагнетик в отсутствие поля (а) и во внешнем магнитном поле (б)  

атомов ориентированы беспорядочно, и поэтому намагниченность равна нулю. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю. Полной ориентации препятствует тепловое движение атомов, которое стремится разбросать моменты. В результате такой преимущественной ориентации парамагнетик намагничивается, создавая собственное магнитное поле, которое, накладываясь на внешнее, усиливает его. Этот эффект называется парамагнитным эффектом или парамагнетизмом.

Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе. Реальные объекты могут обладать как положительными, так и отрицательными магнитными восприимчивостями. Примером веществ с отрицательной восприимчивостью могут служить диамагнетики — их намагниченность по направлению противоположна приложенному магнитному полю. Положительной восприимчивостью обладают, например, парамагнетики и ферромагнетики.

Ферромагнетики – твердые кристаллические вещества, обладающие самопроизвольной (спонтанной) намагниченностью в отсутствие внешнего магнитного поля. Атомы (молекулы) таких веществ обладают отличным от нуля магнитным моментом. В отсутствие внешнего поля магнитные моменты в пределах больших областей ориентированы одинаково (подробнее об этом будет сказано далее). В отличие от слабомагнитных диа- и парамагнетиков ферромагнетики - это сильномагнитные вещества. Для ферромагнетиков характерно явление гистерезиса. Существенной особенностью ферромагнетиков являются огромные величины магнитной проницаемости и магнитной восприимчивости В середине XIX в. было открыто два магнитомеханических эффекта, свойственных ферромагнетикам. Первый из них – это магнитострикция – изменение формы и размеров тела при его намагничивании.

Второй магнитомеханический эффект – это эффект Виллари – изменение и даже исчезновение остаточной намагниченности тела при его сотрясении или деформации. Доменная структура ферромагнетиков.

Классическая теория ферромагнетизма была развита французским физиком П.Вейсом (1907 г.). Согласно этой теории, весь объем ферромагнитного образца, находящегося при температуре ниже точки Кюри, разбит на небольшие области – домены,– которые самопроизвольно намагничены до насыщения.

Доменная структура позволяет объяснить наличие у ферромагнетиков явления гистерезиса. Если на размагниченный образец подействовать внешним магнитным полем, то домены, ориентированные по полю, будут находиться в наиболее выгодном положении. Доменная структура хорошо объясняет также наличие точки Кюри у ферромагнетиков. Неудивительно, что практически совершенный порядок в расположении магнитных моментов атомов при увеличении температуры должен нарушаться. Возрастающее тепловое движение атомов стремится разбросать магнитные моменты, что и происходит при температуре Кюри.

Ферромагнетики широко применяются в различных областях науки, в промышленности, медицине.

13) электромагнитная индукция – явление возникновения электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур.

ЭДС индукции в замкнутом контуре равна модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

закон Фарадея - Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

Это выражение представляет собой основной закон электромагнитной индукции.

Самоиндукция- явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой цепи. Индуктивность – коэффициент пропорциональности между силой тока в контуре и магнитным потоком, создаваемым этим током:

Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, ε_i в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности:

. Явление взаимной индукции. @

Рассмотрим два контура 1 и 2, расположенные близко друг от друга (рис. 3.3). Пусть в контуре 1 течет ток I₁. Он создает магнитный поток, пронизывающий контур 2 и пропорциональный величине самого тока I₁:

Ф_m21 = L₂₁I₁.

Направление силовых линий поля В₁, создающего поток Ф_m21 изображено на рис.3.3 сплошными линиями и определяется правилом правой руки. При изменении тока I₁ поток Ф_m21 становится переменным,и в контуре 2 индуцируется э.д.с., равная

Аналогично при протекании тока I₂ в контуре 2 через контур 1 возникает магнитный поток Ф_m12 , пронизывающий контур 1: Ф_m12= L₁₂I₂.

Магнитное поле этого потока В₂ изображено на рис.3.3 пунктирными линиями. Как и в первом случае, при изменениях тока I₂ в контуре 1 индуцируется э.д.с., равная

I₁

В₁

В₂

I₂

Рис. 3.3. Явление взаимной индукции

Контуры 1 и 2 называются связанными, а явление возникновения э.д.с. в одном из них при изменении силы тока в другом - взаимной индукцией.

где L₁₂ и L₂₁ - скалярные величины, равные отношению потокосцепления одного контура к силе тока в другом, обуславливающей это потокосцепление. В отсутствие ферромагнетиков для любых двух связанных контуров коэффициенты взаимной индукции равны друг другу:

.

Взаимная индуктивность также измеряется в генри. Величины коэффициентов взаимной индукции определяются геометрической формой, размерами контуров и их относительным расположением. Явление взаимной индукции используется, например, в электрических трансформаторах – устройствах, преобразующих переменный ток одного напряжения в переменный ток другого напряжения.

14) трансформатор- устройство для преобразования напряжения переменного тока, состоящее из двух катушек на общем ферромагнитном сердечнике.

Энергия магнитного поля.

ε

R

L

Рис. 3.4. К определению энергии магнитного поля

Для определения энергии магнитного поля рассмотрим контур, состоящий из источника э.д.с. - ε, катушки индуктивности - L и сопротивления - R При замыкании цепи ток возрастает от 0 до I, и, следовательно, возникает э.д.с. самоиндукции ε_is, направленная против э.д.с. ε, возбуждающей ток. При размыкании цепи сила тока уменьшается от I до 0, что вызывает появление э.д.с. самоиндукции ε_is того же направления, что и направление внешней ε. Можно предположить, что на увеличение тока в контуре затрачивается дополнительная работа, идущая на создание энергии магнитного поля. При снижении тока эта энергия выделяется в виде дополнительного джоуль-ленцева тепла.

. Теория Максвелла для электромагнитного поля. @

известно, равна нулю, поэтому . Итак, циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру L равна взятой с обратным знаком скорости изменения магнитного потока сквозь поверхность S, ограниченную этим контуром.

15)Колебательный контур – система, состоящая из конденсатора и катушки индуктивности, образующих замкнутую электрическую цепь.

Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Доставка через транспортную компанию производится не по указанному Вами адресу, а до представительства транспортной компании в Вашем городе. При выборе этого способа доставки нельзя оплатить заказ наложенным платежом.

Дата добавления: 2015-06-25