
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однородной сцены ( ) вторым методом
|
|
|
|
.
Из Теоремы 3.1.1 следует, что  можно использовать в качестве признака квадратного участка
можно использовать в качестве признака квадратного участка 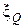 сцены. Очевидно, что при любом изображении
сцены. Очевидно, что при любом изображении 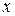 значение
значение 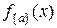 равняется количеству таких оценок
равняется количеству таких оценок 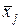 , для которых выполняется неравенство
, для которых выполняется неравенство 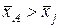 . Поэтому областью значений признака
. Поэтому областью значений признака  является множество
является множество 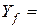
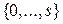 . Для выяснения эффективности признака
. Для выяснения эффективности признака  при поиске зон интереса рассмотрим множество
при поиске зон интереса рассмотрим множество 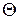 квадратных участков сцены одинаковых размеров, состоящее из двух подмножеств (классов)
квадратных участков сцены одинаковых размеров, состоящее из двух подмножеств (классов) 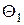 и
и 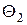 . Класс
. Класс 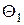 состоит только из зон интереса. Класс
состоит только из зон интереса. Класс 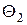 состоит из квадратных участков, являющихся фрагментами однородных случайных полей. Такие участки содержат только фон. Покажем, что для локально однородных сцен, полученных скользящим суммированием по окрестности с радиусом
состоит из квадратных участков, являющихся фрагментами однородных случайных полей. Такие участки содержат только фон. Покажем, что для локально однородных сцен, полученных скользящим суммированием по окрестности с радиусом 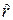 , имеет место следующий результат.
, имеет место следующий результат.
Теорема 4.2.1. Пусть 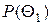 и
и 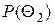 - априорные вероятности классов
- априорные вероятности классов 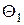 и
и 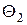 ,
, 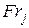 ,
, 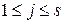 , - связные фрагменты границы
, - связные фрагменты границы  , содержащие по
, содержащие по 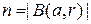 пикселей и такие, что
пикселей и такие, что 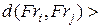 2
2 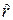 , а
, а  - признак квадрата
- признак квадрата 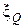 , соответствующий
, соответствующий 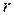 и
и 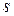 . Тогда для любого
. Тогда для любого 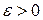 существуют такие
существуют такие 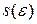 и
и 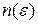 , что вероятность
, что вероятность 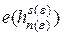 ошибки решающего правила
ошибки решающего правила 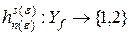 вида
вида

классификации квадратов из 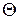 не превосходит
не превосходит 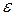 .
.
Таким образом, при достаточно больших значениях 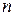 и
и 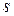 для вероятности ошибки справедливо приближенное равенство
для вероятности ошибки справедливо приближенное равенство 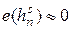 .
.
В приложениях вероятность 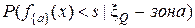 называют вероятностью пропуска зоны интереса, а
называют вероятностью пропуска зоны интереса, а 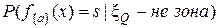 - вероятностью обнаружения ложной зоны.
- вероятностью обнаружения ложной зоны.
Применение Теоремы 4.2.1 для поиска зон интереса предполагает выбор для каждого объекта 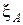 квадратной окрестности
квадратной окрестности 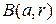 , лежащей в
, лежащей в 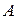 . Покажем, как это можно сделать.
. Покажем, как это можно сделать.
Вначале рассмотрим частный случай, когда проекция 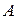 объекта является квадратом со сторонами параллельными осям координат и длиной
объекта является квадратом со сторонами параллельными осям координат и длиной 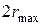 . Пусть
. Пусть 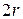 - сторона окрестности квадратной формы, используемой при сглаживании. Очевидно, что
- сторона окрестности квадратной формы, используемой при сглаживании. Очевидно, что 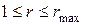 . Выберем произвольную точку
. Выберем произвольную точку 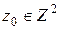 , число
, число 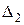 , удовлетворяющее неравенству
, удовлетворяющее неравенству 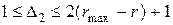 , называемое шагом, и построим на
, называемое шагом, и построим на 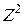 семейство квадратов
семейство квадратов 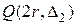 со сторонами равными
со сторонами равными 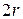 и координатами
и координатами 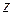 левых верхних вершин, определяемыми равенством
левых верхних вершин, определяемыми равенством
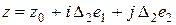 ,
, 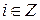 ,
, 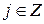 .
.
В этом случае справедливо следующее утверждение.
Теорема 4.2.2. Всегда существует квадрат 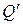 из семейства
из семейства 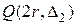 такой, что
такой, что 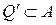 .
.
Из Теоремы следует, что максимальная величина шага равняется 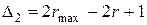 и не зависит от
и не зависит от 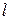 .
.
4.3 Эксперименты с локально однородными сценами
Для иллюстрации рассмотренных методов поиска зон интереса, воспользуемся фрагментом локально однородной сцены. Ее проекцией служит квадрат со стороной, равной 511 масштабным единицам (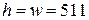 ) или 512 пикселям. Фрагмент состоит из 20 объектов. Девятнадцать объектов имеют прямоугольные проекции со сторонами 29 и 14 масштабных единиц, случайные координаты и ориентацию. Каждый объект является участком однородного случайного поля, со средним значением
) или 512 пикселям. Фрагмент состоит из 20 объектов. Девятнадцать объектов имеют прямоугольные проекции со сторонами 29 и 14 масштабных единиц, случайные координаты и ориентацию. Каждый объект является участком однородного случайного поля, со средним значением 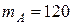 и корреляционной функцией
и корреляционной функцией 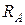 , заданной таблицей 2.2. Остальные пиксели фрагмента образуют двадцатый объект, который будет называться фоном. Он также является участком однородного случайного поля со средним значением
, заданной таблицей 2.2. Остальные пиксели фрагмента образуют двадцатый объект, который будет называться фоном. Он также является участком однородного случайного поля со средним значением 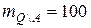 и той же самой корреляционной функцией. Однородные случайные поля для каждого объекта и фона строятся по способу, описанному в 2.3, то есть скользящим суммированием по квадратной окрестности с радиусом
и той же самой корреляционной функцией. Однородные случайные поля для каждого объекта и фона строятся по способу, описанному в 2.3, то есть скользящим суммированием по квадратной окрестности с радиусом 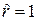 . При указанных средних значениях и дисперсиях отношение сигнал/шум в окрестности каждого из девятнадцати объектов составляет величину
. При указанных средних значениях и дисперсиях отношение сигнал/шум в окрестности каждого из девятнадцати объектов составляет величину 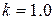 . Одно из возможных изображений фрагмента приведено на рисунке 4.1. По нему можно достаточно уверено построить зону интереса для каждого объекта визуальным способом.
. Одно из возможных изображений фрагмента приведено на рисунке 4.1. По нему можно достаточно уверено построить зону интереса для каждого объекта визуальным способом.

|
Рисунок 4.1 - Изображение локально однородной сцены
(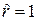 , , 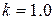 ) )
|
Для проведения компьютерных экспериментов по поиску зон интереса требуется знать диаметр 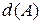 объектов, длину
объектов, длину 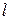 стороны зоны интереса, количество
стороны зоны интереса, количество 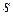 фрагментов границы, радиус сглаживания
фрагментов границы, радиус сглаживания 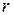 и шаг
и шаг 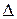 . Значение
. Значение 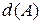 , вычисленное по прямоугольной проекции с указанными выше размерами, равняется
, вычисленное по прямоугольной проекции с указанными выше размерами, равняется 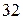 единицам. Так как фон является однородным случайным полем, то
единицам. Так как фон является однородным случайным полем, то 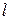 ограничена сверху только минимальным рас-
ограничена сверху только минимальным рас-
стоянием между объектами. Их расположение позволяет выбрать значение 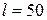 . Количество
. Количество 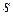 фрагментов границы влияет на вероятность обнаружения ложной зоны. В экспериментах использовалось
фрагментов границы влияет на вероятность обнаружения ложной зоны. В экспериментах использовалось 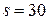 . Для вычисления оценок
. Для вычисления оценок 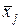 ,
, 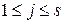 , применялись фрагменты границы, состоящие из девяти пикселей. Это соответствует квадратной окрестности с минимальным радиусом
, применялись фрагменты границы, состоящие из девяти пикселей. Это соответствует квадратной окрестности с минимальным радиусом 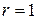 .
.
При использовании 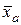 в качестве оценки неизвестного среднего значения
в качестве оценки неизвестного среднего значения 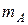 объекта максимальный шаг вычисляется, в соответствии с Теоремой 4.2.2, по формуле
объекта максимальный шаг вычисляется, в соответствии с Теоремой 4.2.2, по формуле 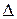 =
= 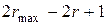 , то есть зависит от радиуса сглаживания
, то есть зависит от радиуса сглаживания 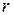 . При указанных размерах проекций объектов
. При указанных размерах проекций объектов 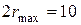 . Поэтому максимальное значение
. Поэтому максимальное значение 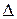 =9 достигается при минимальном радиусе
=9 достигается при минимальном радиусе 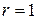 . Следовательно,
. Следовательно, 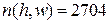 квадратов. В ходе классификации 158 квадратов из этого числа были классифицированы в качестве зон интереса (реальных и ложных). Таким образом, количество подлежащих сегментации квадратов удалось уменьшить более, чем в семнадцать раз.
квадратов. В ходе классификации 158 квадратов из этого числа были классифицированы в качестве зон интереса (реальных и ложных). Таким образом, количество подлежащих сегментации квадратов удалось уменьшить более, чем в семнадцать раз.
В графической форме результаты поиска вторым методом представлены на рисунке 4.2. Зону интереса удалось построить для каждого объекта. Так как на этот раз для каждого объекта в 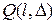 оказалось по шесть зон, то число реальных зон в
оказалось по шесть зон, то число реальных зон в 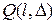 равняется 114. Из них удалось обнаружить только 54 зоны. Следовательно, относительная частота правильной классификации зоны интереса равняется 54/114=0.474. Относительная частота ложного распознавания зоны составляет (158-54)/(2704-114)=0.040. Отметим, что при
равняется 114. Из них удалось обнаружить только 54 зоны. Следовательно, относительная частота правильной классификации зоны интереса равняется 54/114=0.474. Относительная частота ложного распознавания зоны составляет (158-54)/(2704-114)=0.040. Отметим, что при 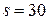 из таблицы 3.1 следует, что вероятность
из таблицы 3.1 следует, что вероятность 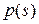 ложного обнаружения зоны интереса бернуллиевских сцен с нормальными распределениями равняется 0.032. Так как 60 зон интереса оказались пропущены и 104 пустых квадрата ошибочно распознаны в качестве зон, то относительная частота ошибки классификации квадратов из
ложного обнаружения зоны интереса бернуллиевских сцен с нормальными распределениями равняется 0.032. Так как 60 зон интереса оказались пропущены и 104 пустых квадрата ошибочно распознаны в качестве зон, то относительная частота ошибки классификации квадратов из 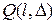 равняется 0.061.
равняется 0.061.
Полученное в эксперименте значение 0.474 относительной частоты правильной классификации зон интереса нельзя считать неудачей. В самом деле, решение о том, что квадрат является зоной интереса принимается только при условии, что средняя яркость 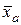 , вычисленная для центрального пикселя, превышает все
, вычисленная для центрального пикселя, превышает все 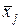 ,
, 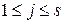 . Однако при шаге
. Однако при шаге 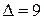 семейство
семейство
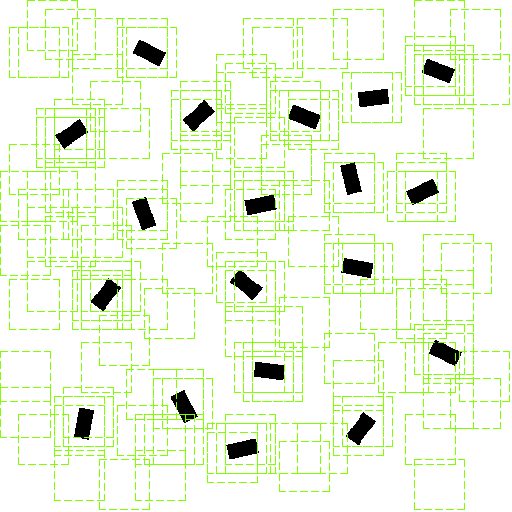
|
Рисунок 4.2 - Результаты поиска зон интереса на локально однородной сцене с использованием оценки 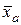 ( (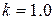 , , 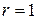 ) )
|
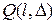 содержит по шесть зон интереса для каждого объекта. У более половины этих зон условие
содержит по шесть зон интереса для каждого объекта. У более половины этих зон условие 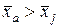 ,
, 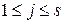 , не выполняется потому, что окрестность
, не выполняется потому, что окрестность 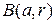 частично или полностью состоит из пикселей фона. С другой стороны, в соответствии с Теоремой 4.2.2, для каждого объекта в
частично или полностью состоит из пикселей фона. С другой стороны, в соответствии с Теоремой 4.2.2, для каждого объекта в 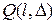 присутствует зона интереса, хотя бы одна, для которой выполняется условие
присутствует зона интереса, хотя бы одна, для которой выполняется условие 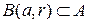 . По Теореме 3.4.1 вероятность правильного распознавания таких зон при достаточно большом значении
. По Теореме 3.4.1 вероятность правильного распознавания таких зон при достаточно большом значении 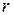 равна, практически, единице. Для рассматриваемой сцены зону интереса удалось построить для каждого объекта даже при минимальном значении
равна, практически, единице. Для рассматриваемой сцены зону интереса удалось построить для каждого объекта даже при минимальном значении 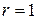 .
.
А теперь рассмотрим результаты поиска зон интереса на более сложной сцене. На рисунке 4.3 представлено изображение фрагмента локально однородной сцены, который отличается от предыдущего только величиной отношения сигнал/шум. В самом деле, при уменьшении среднего значения 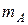 со 120 до 110 отношение сигнал/шум
со 120 до 110 отношение сигнал/шум 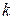 уменьшилось с 1.0 до 0.5. Построение зон интереса визуальным способом по такому изображению требует заметных усилий и времени.
уменьшилось с 1.0 до 0.5. Построение зон интереса визуальным способом по такому изображению требует заметных усилий и времени.
К сожалению, построить зону интереса для каждого объекта, когда при вычислении оценок 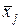 ,
, 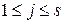 , использовались фрагменты, содержащие по 9 пикселей (это соответствуют минимальному радиусу сглаживания
, использовались фрагменты, содержащие по 9 пикселей (это соответствуют минимальному радиусу сглаживания 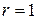 ), не удалось. Это означает, что для сцены, сложность которой измеряется величиной
), не удалось. Это означает, что для сцены, сложность которой измеряется величиной 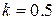 , минимальная окрестность, состоящая из девяти пикселей, не обеспечивает нужной точности вычисления оценок неизвестных средних значений. Поэтому были проведены дополнительные эксперименты, в которых использовались окрестности, из 25 и 49 пикселей, что соответствует радиусам сглаживания
, минимальная окрестность, состоящая из девяти пикселей, не обеспечивает нужной точности вычисления оценок неизвестных средних значений. Поэтому были проведены дополнительные эксперименты, в которых использовались окрестности, из 25 и 49 пикселей, что соответствует радиусам сглаживания 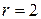 и 3. Полученные результаты приведены в таблице 4.1. Для каждого
и 3. Полученные результаты приведены в таблице 4.1. Для каждого 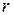 указано количество
указано количество
Таблица 4.1 - Результаты поиска зон интереса по изображению локально
(r, 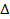 ) )
| (1,9) | (2,7) | (3,5) |
| n (h,w) | |||
| nQ | |||
| nA |

|
Рисунок 4.3 - Изображение локально однородной сцены
(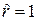 , , 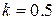 ) )
|
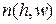 квадратов в
квадратов в 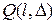 , количество
, количество 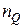 квадратов из
квадратов из 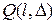 , классифицированных в качестве зон интереса и количество
, классифицированных в качестве зон интереса и количество  объектов, для которых удалось построить зону интереса. Из представленных данных следует, что при
объектов, для которых удалось построить зону интереса. Из представленных данных следует, что при 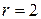 и 3 удалось построить зоны интереса для каждого объекта. Напомним, что количество
и 3 удалось построить зоны интереса для каждого объекта. Напомним, что количество 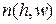 квадратов в семействе
квадратов в семействе 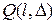 на прямоугольном фрагменте высотой
на прямоугольном фрагменте высотой  и шириной
и шириной  , зависит от величины шага
, зависит от величины шага 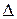 . При увеличении
. При увеличении 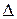 в
в 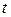 раз
раз 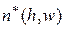 уменьшается в
уменьшается в 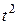 раз.
раз.
4.4 Зоны интереса на бернуллиевских сценах
Очевидно, что все сказанное в 4.2 верно и для бернуллиевских сцен.
По определению, пиксели бернуллиевских сцен являются независимыми в совокупности случайными величинами. Этим свойством можно воспользоваться для построения методов классификации квадратов, основанных на теории проверки статистических гипотез.
Пусть 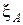 - пятно с диаметром
- пятно с диаметром 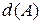 , средним значением
, средним значением  и дисперсией
и дисперсией 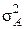 ,
, 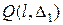 - семейство квадратов, определенное для
- семейство квадратов, определенное для 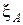 изложенным в 4.1 способом и
изложенным в 4.1 способом и 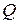 - квадрат из
- квадрат из 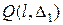 . Предположим (гипотеза), что случайные величины, образующие семейство
. Предположим (гипотеза), что случайные величины, образующие семейство 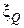 , имеют одно и то же распределение вероятностей со средним значением
, имеют одно и то же распределение вероятностей со средним значением 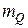 и дисперсией
и дисперсией 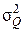 . Это означает, что
. Это означает, что 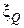 не является зоной интереса. Из определения бернуллиевской сцены следует, что изображения границы
не является зоной интереса. Из определения бернуллиевской сцены следует, что изображения границы 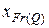 и зоны интереса без границы
и зоны интереса без границы 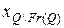 являются реализациями случайных выборок. Поэтому на основании центральной предельной теоремы выборочные средние
являются реализациями случайных выборок. Поэтому на основании центральной предельной теоремы выборочные средние 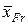 и
и 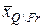 , а также их разность
, а также их разность 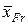 -
- 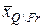 являются асимптотически нормальными случайными величинами с параметрами
являются асимптотически нормальными случайными величинами с параметрами
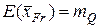 и
и 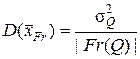 ,
,
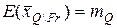 и
и 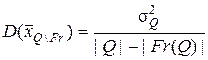 ,
,
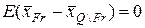 и
и 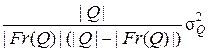 .
.
Выберем в качестве 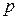 положительное число достаточно близкое к нулю (например, 0.05, 0.01 или еще меньше) и найдем
положительное число достаточно близкое к нулю (например, 0.05, 0.01 или еще меньше) и найдем 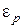 из уравнения
из уравнения
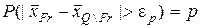 .
.
Для этого заменим 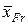 -
- 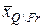 нормированной случайной величиной
нормированной случайной величиной
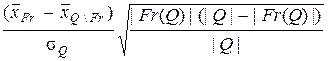 ,
,
и воспользуемся интегралом вероятностей
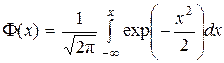 .
.
Он позволяет записать уравнение 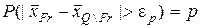 в виде
в виде
2  .
.
Таким образом, для вычисления границ - 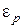 и
и 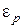 критической области
критической области 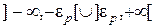 остается воспользоваться таблицей интеграла вероятностей.
остается воспользоваться таблицей интеграла вероятностей.
Очевидно, что при верной гипотезе событие 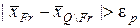 является маловероятным. Это позволяет сформулировать решающее правило для классификации квадратов
является маловероятным. Это позволяет сформулировать решающее правило для классификации квадратов 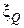 из
из 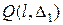 в следующем виде. Если для
в следующем виде. Если для 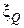 выполняется неравенство
выполняется неравенство 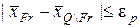 , то
, то 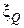 не является зоной интереса. В противном случае, когда
не является зоной интереса. В противном случае, когда 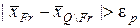 , квадрат
, квадрат 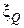 является зоной интереса для
является зоной интереса для 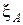 . Очевидно, что вероятность правильной классификации квадрата без объекта равняется
. Очевидно, что вероятность правильной классификации квадрата без объекта равняется 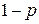 , а вероятность обнаружения ложной зоны интереса -
, а вероятность обнаружения ложной зоны интереса - 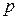 .
.
Заметим, что для вычисления 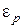 необходима дисперсия
необходима дисперсия 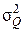 . Если она неизвестна, то можно воспользоваться ее оценкой
. Если она неизвестна, то можно воспользоваться ее оценкой 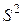 или ее несмещенным вариантом
или ее несмещенным вариантом 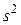 , которые определяются равенствами
, которые определяются равенствами
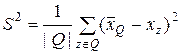 и
и 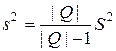 ,
,
используя в качестве реализации выборки изображение 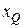 всей зоны.
всей зоны.
В качестве примера на рисунке 4.3 приведено одно из изображений фрагмента бернуллиевской сцены размером 511 на 511 масштабных единиц. Фрагмент содержит 19 объектов прямоугольной формы со сторонами 29 и 14 масштабных единиц, расположенных на тех же местах и с той же ориентацией, что и на фрагменте, изображения который представлен на рисунке 4.1. Однако пиксели сцены (объектов и фона) имеют равномерное распределение со средними значениями 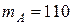 и
и 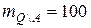 соответственно, одной и той же дисперсией
соответственно, одной и той же дисперсией 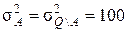 . Поэтому
. Поэтому 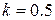 . При радиусе сглаживания
. При радиусе сглаживания 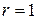 относительная частота количества объектов, для которых удалось построить зоны интереса по этому изображению, составила 0.53.
относительная частота количества объектов, для которых удалось построить зоны интереса по этому изображению, составила 0.53.

|
Рисунок 4.4 - Изображение фрагмента бернуллиевской сцены (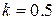 ) )
|
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 364; Нарушение авторских прав?; Мы поможем в написании вашей работы!