Формулы

Расчёт трёхшарнирной арочной фермы

Расчёт трёхшарнирной арки

Схема арки Исходные данные

Размеры, м	Расч. нагрузка
L	f	q, кН/м	Р, кН

y = 4fx(l-x)/ L² - парабола

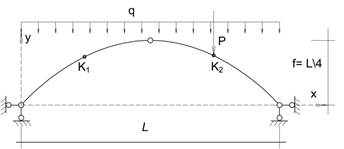
Требуется:

1. Вручную определить опорные реакции и внутренние усилия в арке: изгиб, моменты, поперечные

и продольные силы в т. К1 и К2, расположенных в четвертях пролёта.

2. Расчётом на ПК определить опорные реакции и внутренние усилия: изгиб, моменты, поперечные

и продольные силы во всех точках.

Исполнитель: студент ______________________________________ курса _______ группы

Срок выполнения ___________________ Преподаватель: Мещеряков Ю.М.

_____________________________________________________________________________________________

Задание №1 по статике сооружений Вариант 12

Схема фермы Исходные данные

Размеры, м	Расч. нагрузка
L	Р, кН

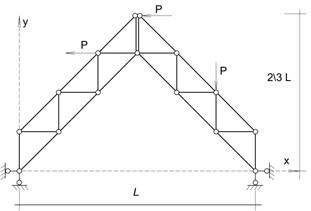
Требуется:

1. Вручную определить опорные реакции и продольные силы в стержнях арочной фермы

в сечениях1-1 и 2-2.

2. Расчётом на ПК определить опорные реакции и продольные силы во всех стержнях арочной фермы.

Исполнитель: студент____________________________________ курса _______ группы

Срок выполнения _______________ Преподаватель: Мещеряков Ю.М.

по дисциплине «Математические методы в исторических исследованиях»

Средняя арифметическая () – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле:

,

где x_i - варианта с порядковым номером ( =1,… n); n – объем совокупности.

Мода (Мо) – варианта, которая чаще всего встречается в данном вариационном ряду.

Медиана (Ме) – варианта, находящаяся в середине вариационного ряда:

Ме = , если число вариант нечетно (n =2 m +1);

Ме = , если число вариант четно (n =2 m).

Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака:

Дисперсия (s ²) – абсолютная мера вариации (колеблемости) признака в статистическом ряду – средний квадрат отклонения всех значений признака ряда от средней арифметической этого ряда:

,

где x_i – варианта с порядковым номером ; – средняя арифметическая;

n – объем совокупности.

Среднее квадратическое отклонение (s) – это квадратный корень из дисперсии:

Коэффициент вариации (V) – это отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:

Величина ошибки выборки – это разность между генеральной и выборочной средними.

Средняя ошибка выборки (m) при случайном повторном отборе определяется формулой:

= ,

где s – оценка среднего квадратического отклонения в генеральной совокупности по выборке; n – объем выборки.

Средняя ошибка малой выборки, т.е. выборки, объем которой не превышает 30 единиц, вычисляется по формуле:

=

Предельная ошибка выборки (D) вычисляется по формуле:

D=tm,

где t – коэффициент, вычисляемый по специальной таблице; m – средняя ошибка выборки.

Доверительный интервал определяется по формуле:

,

Парный линейный коэффициент корреляции определяет тесноту связи между двумя признаками и рассчитывается по формуле:

,

где – значения признаков x и y для i -го объекта; n – число объектов; – средние арифметические значения признаков x и y.

Коэффициент детерминации – показатель, определяющий долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака:

,

где r – коэффициент корреляции.

Уравнение регрессии – это описание корреляционной связи с помощью подходящей функции.

Простейшее уравнение линейной регрессии имеет вид:

,

где x – факторный признак; y – результативный признак; a и b – параметры уравнения, которые могут быть найдены методом наименьших квадратов по формулам:

,

где – -е значение признаков x и y соответственно; - средние арифметические признаков x и y; n - число значений признаков x и y.

Формулы цепных и базисных индексов*

Абсолютные приросты	Темпы роста	Темпы прироста
цепные	базисные	цепные	базисные	цепные	базисные
xt – xt–1	xt – x1	xt / xt–1	xt / x1	(xt – xt–1)/ xt–1	(xt – x1)/ x1

Здесь t изменяется от 2 до n, где n – число членов ряда.

Средний абсолютный прирост показывает, насколько быстро в среднем за период изменяется конечный уровень ряда относительно первоначального, и вычисляется по формуле:

Dx = (x_n – x₁)/(n –1),

где xn и x1 – последний и первый уровни ряда соответственно.

Дата добавления: 2015-06-04