
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Библиографический список. 1. Биркгоф Г. Современная прикладная алгебра/г. Биркгоф, Т. Барти – М. : мир, 1976
1. Биркгоф Г. Современная прикладная алгебра/Г.Биркгоф, Т.Барти – М.: Мир, 1976. - 400 с.
2. Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов/ И.Н.Бронштейн, К.А. Семендяев - Лейпциг: Тайбнер, М.: Наука, 1981. – 718 с.
3. Горбатов В.А. Основы дискретной математики/ В.А.Горбатов. – М.: Высш. шк., 1986. – 311 с.
4. Кемени Дж. Введение в конечную математику/ Дж.Кемени, Дж. Снелл, Дж. Томпсон. – М.: Изд-во иностранной литературы, 1963. – 486 с.
5. Коршунов Ю.М. Математические основы кибернетики/Ю.Коршунов – М.: Энергия, 1972. – 376 с.
6. Кузнецов О.П. Дискретная математика для инженера/ О. Кузнецов, Г. Адельсон - Вельский. – М.: Энергоатомиздат, 1988. – 480 с.
7. Кук Д. Компьютерная математика/ Д.Кук, Г. Бейз. – М.: Наука, 1990. – 384 с.
8. Куратовский К. Теория множеств/ К.Куратовский, А.Мостовский - М.: Мир, 1970. – 416 с.
9. Ренин С.В. Основы дискретной математики/ С. В.Ренин - Новосибирск: Новосибирский электротехнический институт, 1981. – 43 с.
10. Ренин С.В. Сб. задач и упражнений по основам теории систем/ С.В.Ренин - Новосибирск: Новосибирский электротехнический институт, 1981. - 48 с.
е) Х = Z 2 ´ Z 2, Р = {((x, y), (u, v)): x*v = y*u}, Q = {((x, y), (u, v)): x + u =
= y + v};
ж) X Î R, P = {(x, y): x £ y}, Q = {(x, y): x < y}?
Указать тип этих отношений.
3.37. Какими свойствами обладают отношения (Х, Р) и (Х, Р-1), где Х – множество людей, если:
а) P = {(x, y): х моложе у}, б) P = {(x, y): х – ребенок у}, в) P = {(x, y): х состоит в браке с у}, г) P = {(x, y): х живет в одном городе с у}, д) P = {(x, y): х – брат у}, е) P = {(x, y): х – предок у}, ж) P = {(x, y): х и у имеют одних и тех же родителей}, з) P = {(x, y): х и у имеют общего предка}.
3.38. Пусть отношения S и Т определены на множестве всех людей Х следующим образом: S = {(x, y) Î Х2: х является отцом у}, Т = {(x, y) Î Х2: х – дочь у}. Описать явно следующие отношения:
а) S2, б) Т2, в) 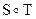 , г)
, г) 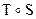 , д)
, д) 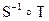 , е)
, е) 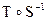 , ж)
, ж) 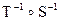 , з)
, з) 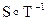 , и)
, и) 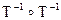 , к)
, к) 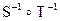 .
.
3.39. Пусть имеется некоторая программа, которая читает два числа из множества А = {1, 2, 3, 4, 5}, обозначаемых х и у, и, если х < у, печатает число z Î А, такое, что x £ z < y. В любом случае, программа останавливается после считывания всех чисел из А. Задача определяет отношение Р Í А2, такое, что
Р = {(x, y), z: x < y, x £ z < y}. Найти область определения и область значений этого отношения.
3.40. Показать, что отношение i £ j на множестве {1, 2, 3, …, n} задается треугольной матрицей.
СОДЕРЖАНИЕ
| 1. | Теоретический раздел....................................... | |
| 2. | Примеры решения типовых задач............................ | |
| 3. | Задачи для упражнений..................................... | |
| Библиографический список................................. |
|
|
Дата добавления: 2015-06-26; Просмотров: 423; Нарушение авторских прав?; Мы поможем в написании вашей работы!