Виды средних

Средние величины делят на два больших класса:

1. Степенные средние – средняя геометрическая, арифметическая, квадратическая и т.д.;

2. Структурные средние – мода и медиана.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя исчисляется по несгруппированным данным и имеет вид:

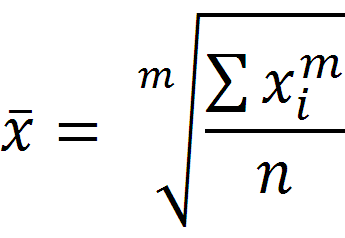
где x_i – варианта (значение) осредняемого признака;

m – показатель степени средней;

n – число вариант.

Взвешенная средняя считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:

где x_i – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

m – показатель степени средней;

f_i – частота, показывающая, сколько раз встречается i-е значение осредняемого признака.

В зависимости от показателей степени m различают следующие виды степенных средних:

Средняя гармоническая – m = -1;

Средняя геометрическая – m → 0;

Средняя арифметическая – m = 1;

Средняя квадратическая – m = 2;

Средняя кубическая – m = 3 и т.д.

Правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

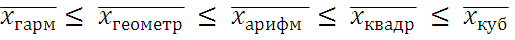
и т.д.

Пример: Расчет среднего возраста студентов в группе из 20 человек.

№ п/п	Возраст

Средний возраст рассчитывается по формуле простой средней:

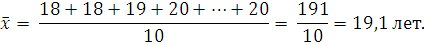
Сгруппируем данные. Получим следующий ряд распределения:

Возраст, x лет				Всего
Число студентов

В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте X лет. Средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:

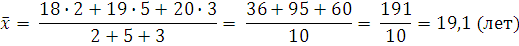
Средняя гармоническая имеет более сложную конструкцию. Чаще всего применяют тогда, когда в качестве весов используется не единицы совокупности носители признака, а произведения этих единиц на значения признака (т.е. m = x f).

Например: Есть данные о реализации продукции одного вида на трех рынках города:

Рынки	Цена за ед. продукта (руб.) Х	Количество продаваемой продукции (шт.) f
Итого	-

Цены выступают в качестве вариант, а количество проданного товара – в качестве весов. Тогда средняя цена определяется по средней арифметической взвешенной:

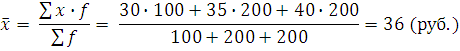
Теперь предположим, что нам известны цены и выручка от продажи. В этом случае расчет ведется в форме средней гармонической взвешенной. Обозначим: x f = M, тогда f = M / x. Подствим в формулу средней арифметической взвешенной вместо f x – M, вместо f – M/x, получим формулу средней гармонической взвешенной:

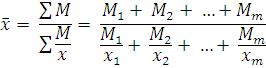
Рынки	Цена за ед. продукта (руб.) Х	Выручка от продажи в руб. М
Итого	-

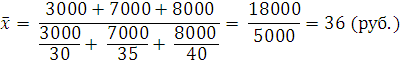
Пример: В результате проверки двух партий муки установлено:

Партия	Вес муки высшего сорта (кг)	Процент от общего веса партии (%)
		70,4
		78,6
Итого		-

Необходимо определить процент муки высшего сорта в среднем по 1 и 2 партиям вместе.

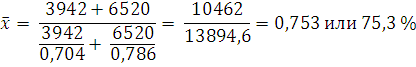
Дата добавления: 2015-06-26