
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет параметров оптимальной динамической настройки САР различными методами
|
|
|
|
Расчет настройки основного регулятора с использованием метода
«Золотого Сечения» (МЗС)
- Находим по формуле (25) относительную постоянную времени опережающего участка:
 (25)
(25)
- Находим относительный коэффициент усиления регулятора (формула (23), где А 1=2,56, А 2=1,618 − коэффициенты Вышнеградского с уточнением по ПЗС:

- Находим абсолютное значение коэффициента усиления регулятора:
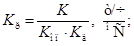
- Находим относительное время интегрирования по формуле (24):

- Находим абсолютное значение времени интегрирования:

- Записываем передаточную функцию основного регулятора:
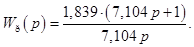
На рисунке представлена блок-схема САР с учетом метода «Золотого сечения».
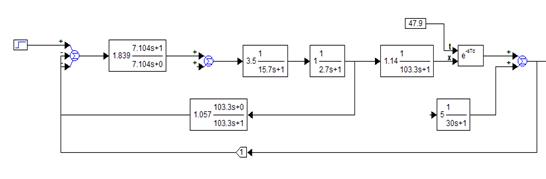 |
Блок-схема схема типовой САР с дифференциатором
с учетом МЗС
Методика и расчет параметров оптимальной динамической
настройки САР методом ВТИ
Передаточные функции опережающего и инерционного участков объекта регулирования представлены в виде инерционного звена первого порядка с запаздыванием по методу Кумпфмюллера:
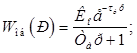 (26)
(26)
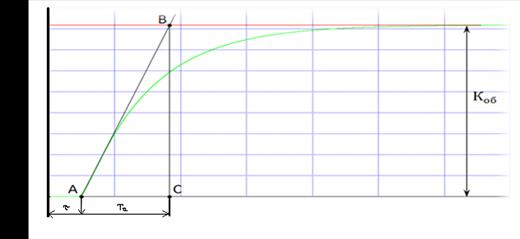
Обработка переходной характеристики объекта методом
Кумпфмюллера
1. Передаточная функция опережающего участка объекта регулирования (ОР):
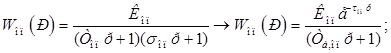 (27)
(27)
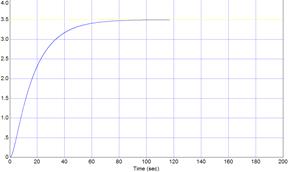
Обработка опережающего участка ОР
2. Передаточная функция инерционного участка объекта регулирования:
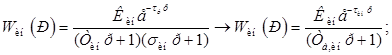 (28)
(28)

Обработка инерционного участка ОР
3. Расчет настроек основного регулятора: 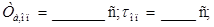 (Определяем по передаточной функции объекта методом Кумпфмюллера! Т.е. строим касательную и определяем Та и τ)
(Определяем по передаточной функции объекта методом Кумпфмюллера! Т.е. строим касательную и определяем Та и τ)

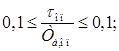


4. Расчет настроек дифференциатора (если он есть) (формулы (29) – (33)):
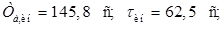
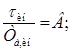
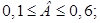
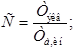 (29)
(29)

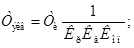 (30)
(30)
 (31)
(31)
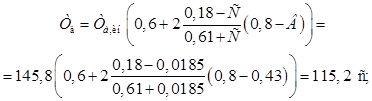 (32)
(32)
 (33)
(33)



Блок-схема САР по методу ВТИ представлена на рисунке.
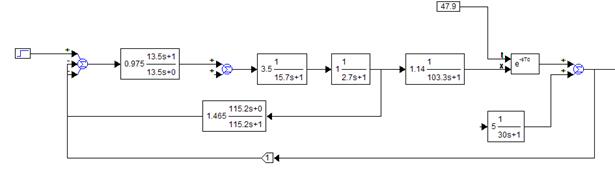
Блок-схема схема САР с дифференциатором по ВТИ
Методика структурно-параметрической оптимизации предлагаемой
САР на основе передаточной функции оптимального регулятора

Структурная схема САР на основе оптимального
регулятора
Физическая сущность структурно параметрической оптимизации комбинированной КСАР заключается в объединении КСАР и САР с Д за счёт того, что для борьбы с внутренним возмущением используется СР как в каскадной САР, а основной регулятор превращается в корректирующий, структура которого и параметры оптимальной динамической настройки определяются на основе передаточной функции оптимального регулятора, куда входят передаточная функция обратная передаточной функции эквивалентного объекта и желаемая передаточная функция ЗСАР при отработке скачка задания.
Для получения оптимального качества регулирования наиболее важным является выбор рациональной структуры САР, а затем уже и подбор параметров оптимальной динамической настройки. В данном случае, Т зд1 и Т зд2 выбираются по методу «Золотого Сечения» вместо четырёх параметров оптимальной динамической настройки в реальном ПИД-регуляторе (формула (9.22)): К д, Т д, Т и, Т б.
 (9.22)
(9.22)
где 
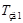 выбираем в соответствии с численным рядом метода «Золотого Сечения», исходя из допустимой величины значения максимального регулирующего воздействия, при этом в данном случае за целую величину принимаем
выбираем в соответствии с численным рядом метода «Золотого Сечения», исходя из допустимой величины значения максимального регулирующего воздействия, при этом в данном случае за целую величину принимаем 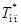 .
.
Принимаем  т.к. при данном значении переходной процесс во внутреннем контуре оптимален и без перерегулирования. Передаточные функции рассчитываем по формулам (9.23) – (9.27).
т.к. при данном значении переходной процесс во внутреннем контуре оптимален и без перерегулирования. Передаточные функции рассчитываем по формулам (9.23) – (9.27).
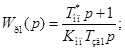 (9.23)
(9.23)
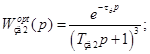 (9.24)
(9.24)
 (9.25)
(9.25)
 (9.26)
(9.26)
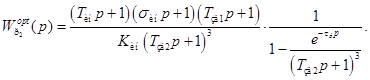 (9.27)
(9.27)
Т зд2 выбираем в соответствии с численным рядом метода «Золотого Сечения», исходя из допустимой величины значения максимального регулирующего воздействия, при этом в данном случае за целую величину принимаем 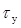 .
.
Проведем анализ для выбора оптимального значения коэффициента при  сравнив несколько значений численного ряда метода «Золотого Сечения»:
сравнив несколько значений численного ряда метода «Золотого Сечения»:
1) 

2) 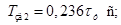
3) 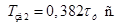
Выбираем 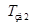 , так чтобы при данном значении Т зд2 переходной процесс системы происходил без видимых колебаний в области высоких частот.
, так чтобы при данном значении Т зд2 переходной процесс системы происходил без видимых колебаний в области высоких частот.
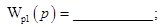

Блок-схема САР на основе оптимального регулятора приведена на рисунке.

Блок-схема схема САР с использованием оптимального
регулятора
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1144; Нарушение авторских прав?; Мы поможем в написании вашей работы!