Проверка прогибов с прямым расчетом

(1) Если расчет необходим, следует рассчитать прогиб при условиях нагрузки, соответствующих цели проверки.

(2)Р Принятый метод расчета должен описывать истинное поведение конструкции при соответствующих воздействиях с точностью, которая согласована с целью расчетов.

(3) Элементы, для которых можно исходить из того, что они не нагружены выше уровня, при котором предел прочности бетона при растяжении не превышен для любого сечения элемента, должны рассматриваться как работающие без трещин. Элементы, в которых предполагается появление трещин, но при этом трещины не полностью пересекают сечение, будут находиться в промежуточном положении между состояниями без трещин и с трещинами, полностью пересекающими сечение. Для элементов, преимущественно подверженных изгибу, соответствующий прогноз поведения выражается формулой (7.18):

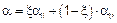(7.18)

где a — рассматриваемый деформационный параметр, который может быть, например, относительной деформацией, кривизной или углом поворота (упрощенно может быть рассмотрен как прогиб (см. (6));

a_I, a_II— значения параметра, рассчитанные для элемента без трещин и с трещинами соответственно;

x — коэффициент распределения (учитывает так называемый эффект ужесточения при растяжении) определяется по формуле

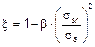, (7.19)

x = 0 — для сечений без трещин;

здесь b — коэффициент, учитывающий влияние на среднюю относительную деформацию длительности нагрузки или повторности нагрузки:

b = 1,0 — при однократном кратковременном нагружении;

b = 0,5 — при постоянных нагрузках или многих циклах повторного нагружения;

s _s — напряжение в растянутой арматуре, которое рассчитывается для сечения
с трещиной;

s _sr — напряжение в растянутой арматуре, которое рассчитывается для сечения
с трещиной при условиях нагружения в момент образования первой трещины.

Примечание — s _s /s _sr может быть заменено на M _cr/ M для изгиба или на N _cr/ N — для чистого растяжения, причем M _cr является моментом трещинообразования, N _cr — усилием трещинообразования.

(4) Деформации от нагрузки могут быть оценены путем использования предела прочности при растяжении и эффективного модуля упругости бетона, см. (5).

Таблица 3.1 содержит диапазон вероятных значений предела прочности при растяжении. Как правило, наилучшие оценки поведения могут быть получены, когда используется средняя прочность при растяжении f_ctm. Если может быть подтверждено, что осевые растягивающие напряжения (например, вызванные усадкой или температурными воздействиями) отсутствуют, может быть использован предел прочности при растяжении с изгибом f_ctm,fl (см. 3.1.8).

(5) Для длительно действующих нагрузок, вызывающих ползучесть, общая деформация, включая деформацию ползучести, определяется с использованием эффективного модуля упругости бетона
по формуле

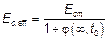, (7.20)

где j(¥, t ₀) — коэффициент ползучести, соответствующий нагрузке и интервалу времени (см. 3.1.4).

(6) Кривизна вследствие усадки определяется по формуле

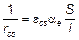, (7.21)

где 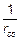— кривизна, вызванная усадкой;

e _cs — свободные относительные деформации усадки (см. 3.1.4);

S — статический момент площади арматуры относительно центра тяжести сечения;

I — момент инерции сечения;

a _e — отношение эффективных модулей упругости:

.

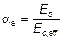S и I, как правило, необходимо определять как для сечения без трещин, так и в состоянии трещинообразования, причем полная кривизна определяется по формуле (7.18).

(7) Наиболее строгим (точным) методом расчета прогиба является метод, указанный в (3), основанный на вычислении кривизны для ряда сечений вдоль длины элемента конструкции и последующем определении прогиба посредством численного интегрирования. В большинстве случаев достаточно рассчитать прогиб дважды, рассматривая весь элемент без трещин и в состоянии с трещинами, а затем интерполировать с использованием формулы (7.18).

Примечание — Если для расчета прогибов используются упрощенные методы, то расчеты должны производиться на основании свойств, приведенных в настоящем техническом кодексе, или определяться при испытаниях.

Дата добавления: 2015-06-26