Частотный анализ поэтических текстов по всем буквам. 1 страница

Лабораторная работа 12

Математизация любой науки связана со следующими двумя уровнями развития. Первый уровень обусловлен переходом науки к абстрактному осмысливанию накопленных фактов и к созданию языка для классификации эмпирических знаний. На втором уровне в языке науки все больше проявляется основное свойство, ради которого он создается, – возможность выражать внутренние закономерности, связи между отдельными фактами и явлениями, изучаемые данной наукой, а также служить орудием познавательной деятельности специалистов. Это требует развития не только выразительных средств языка, но и его исчисленческой стороны, т. е. различного рода формальных (математических) преобразований, которым можно подвергнуть те или иные слова, фразы и другие языковые конструкции.

Таким образом, следует считать, что язык любой науки состоит из двух частей. Первая, основная – это информативная часть языка, непосредственная информация, даже не классифицированная, а просто отобранная каким-то образом совокупность фактов, которые надлежит помнить, чтобы быть эрудированным в данной области знания. Вторая часть – это соответствующее исчисление, под которым, как правило, понимается сжатая форма выражения связей, позволяющих переходить от аксиом к следствиям, от них – к каким-то теоремам, фиксирующим знания в сжатой форме.

Язык математически вводится в язык конкретной науки для выполнения следующих функций:

§ Описание и систематизация знаний;

§ Получение результатов, сопоставимых с экспериментом;

§ Осуществление проверки исходных понятий и функциональных зависимостей между ними;

§ Формулировка законов науки, что дает средства не только для описания и проверки существующего положения, но и для различных видов предсказания.

Математизацию науки можно считать завершенной, если язык этой науки позволяет выполнить все перечисленные функции. К таким наукам можно отнести, прежде всего, физические: отнять у них математику – значит умертвить их.

Однако далеко не во всех науках до сих пор успешно применяются математические методы, хотя, казалось бы, они должны использоваться в любой науке, вступающей в этап абстрактного мышления, поскольку в этом случае наряду с информативной частью языка возникает его исчисленческая часть, позволяющая беспристрастно оценивать факты и явления.

Появление кибернетики и развитие вычислительной техники стимулировало формирование исчисленческой части языка в гуманитарных науках. Например, использование математических методов при изучении естественных языков способствовало возникновению математической лингвистики.

Рассмотрим поэтический текст Н. Рубцова «Видения на холме»:

Взбегу на холм

и упаду

в траву.

И древностью повеет вдруг из дола!

И вдруг картины грозного раздора

Я в этот миг увижу наяву.

Пустынный свет на звёздных берегах

И вереницы птиц твоих, Россия,

Затмит на миг

В крови и в жемчугах

Тупой башмак скуластого Батыя...

Россия, Русь - куда я ни взгляну...
3а все твои страдания и битвы
Люблю твою, Россия, старину,
Твои леса, погосты и молитвы,
Люблю твои избушки и цветы,

И небеса, горящие от зноя,
И шепот ив у омутной воды,
Люблю навек, до вечного покоя...
Россия, Русь! Храни себя, храни!
Смотри, опять в леса твои и долы
Со всех сторон нагрянули они,
Иных времён татары и монголы.
Они несут на флагах чёрный крест,
Они крестами небо закрестили,

И не леса мне видятся окрест,
А лес крестов

в окрестностях

России.

Кресты, кресты...

Я больше не могу

Я резко отниму от глаз ладони

И вдруг увижу: смирно на лугу
Траву жуют стреноженные кони.
Заржут они и где-то у осин
Подхватит эхо медленное ржанье,

И надо мной –

бессмертных звёзд Руси,

Спокойных звёзд безбрежное мерцанье.

В рамках информативной части языка об этом тексте можно сказать следующее.

Это стихотворение во многом программное, в нем сконцентрированы основные мотивы творчес­тва Рубцова. Прежде всего - тема исторической, национальной памяти, помогающая вос­произвести в сознании события от времени Батыя до наших дней. ­3десь и мотив духовной, нравственной крепости народа, сумевшего выстоять в тягчайших испытаниях, отстоять свою независимость, и призыв к современникам исполнять свой долг перед отечеством. Так протягивается нить от Пушкинского стихотворения «Клеветникам России», Лермонтовского «Бородино», Блоковских «Скифов» к стихотворению «Видения на холме» с его особым символическим историко-философским осмыслением новой эпохи. Для Рубцова важно не только то, что выражено словами, но и то, что в под­тексте, не высказано, но напето самой мелодией души. Пригла­шая учиться высокому искусству гармонии у природы, поэт пре­красно понимал жгучую связь между человеком и родной природой, которая может, обо­рвавшись, привести к трагедии, не только экологической, но и нравственной. Отсюда и трагические тона, усиливающие внутрен­ний драматизм его поэзии.

С вышесказанной оценкой текста «Видения на холме» согласится, прежде всего, человек, глубоко любящий родину, переживающий ее невзгоды и радующийся успехам своей страны. Для человека с иными взглядами анализируемый текст не вызовет никаких эмоций и может быть отнесен к обычной посредственности. Вполне очевидно, что оценка поэтических текстов информативным языком страдает субъективностью.

Возникает вопрос: можно ли найти формальные, не субъективные оценки поэтических текстов. С позиции исчисленческой части языка любой текст – это множество (набор) слов. Слова образуют группы слов по какому-либо признаку. В качестве такого признака можно выбрать, например, начальную букву слова. Если число всех слов в тексте обозначить через N₁, а число слов на конкретную начальную букву – через n_i, то можно определить величину

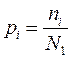(1),

которую назовем частотой появления слова на данную i-ю букву. В число n_i будем включать и слова, состоящие из одной буквы.

По набору частот p_i можно вычислить энтропию информации по известной формуле Шеннона

(2)

Величина Н₁ известна также как количественная мера информации, и она измеряется в битах.

Впервые в [1] этот критерий был использован для количественных оценок поэтических текстов Н. Рубцова. Там же и дана технология обработки текста и проведения расчетов по (2) в программе Microsoft Excel.

Рассчитанная по технологии [1] величина Н₁ для текста «Видения на холме» оказалось равной 4,2077. Само по себе это число пока не о чем не говорит. Однако оказалось, что есть тексты других авторов, энтропия информации которых близка к вышеприведенному числу (см. таблица 1).

Таблица 1

Автор	Название (первая строка)	N1	Н1, бит
Рубцов Н.	Видения на холме		4,2077
Блок А. А.	В ресторане		4,1897
Есенин С. А.	Отговорила роща золотая		4,2539
Лермонтов М. Ю.	Бородино Завещание Пророк Родина Смерть поэта		4,2169 4,1541 4,2091 4,0142 4,0900
Некрасов Н. А.	Кому на Руси жить хорошо		4,0119
Пушкин А. С.	Кипренскому Цветок		4,1177 4, 0646
Фет А. А.	Ель рукавом мне тропинку завесила		4,0298
Цветаева М. И.	Стихи о Москве		4, 1734

Возникает вопрос: что означают близкие числовые значения энтропии информации для текстов различных авторов? Ответ с формальной точки зрения таков: все тексты из таблицы 1 имеют примерно одинаковые средние статистические длины слов.

Вполне очевидно, что неформальный ответ на поставленный вопрос могут давать эксперты, занимающиеся оценкой поэтического творчества.

В [1] произведен расчет Н₁ для сорока пяти поэтических текстов Н. Рубцова. Результаты этих расчетов, заимствованные из [1], воспроизведены в таблице 2. Оказалось, что числовые значения Н₁ для текстов Н. Рубцова изменяются в широких пределах. Возможно, это объясняется и тем обстоятельством, что среди этих текстов есть ранние стихи, как правило, подражательные, более зрелые и, наконец, совершенные, выдвинувшие Н. Рубцова в число лучших поэтов.

Таблица 2

№ номер текст.	Название стихотворения	Колич. слов N1	Н1 бит	Колич. букв N2	H2 бит
	Элегия		3,6294		4,3116
	Ось		4,0043		4,4513
	На вокзале		3,9064		4,4802
	Весна на берегу Бии		4,0055		4,5382
	Прощальная песня		4,0215		4,5462
	В лесу		3,1878		4,3346
	Ветер всхлипывал словно дитя		3,8950		4,3763
	У церковных берез		3,9637		4,4996
	В московском кремле		7,1349		4,4231
	Поэзия		3,4573		4,5084
	Сентябрь		3,7171		4,4649
	По дороге к морю		8,2939		4,6126
	Стоит жара		4,0368		4,4342
	Плыть, плыть		6,4871		4,4778
	Волнуется море		4,1101		4,5217
	Гость молчит и я ни слова		3,7901		4,4911
	В пустыне		3,7915		4,4016

	Увлекаюсь нечаянно		3,4473		4,2204
	В горной деревне		4,0075		4,5289
	Мечты		3,7149		4,4679
	Видения на холме		4,2156		4,4618
	Грани		4,0147		4,1788
	По мокрым скверам проходит осень		3,8397		4,2117
	В полях смеркалось. Близилась гроза		3,6658		4,1651
	Привет Россия		3,9456		3,8839
	В горнице		3,8638		4,3709
	Родная деревня		4,1048		4,4437
	Вологодский пейзаж		4,1059		4,4986
	Далекое		7,1822		4,5458
	На вокзале		3,7422		4,4782
	Старик		3, 7852		4,4542
	Сапоги мои - скрип да скрип		3,8066		4,4202
	Памяти матери		3,8700		4,3806
	В сибирской деревне		4,0113		4,4737
	Зимним вечерком		3,9955		4,4054
	Журавли		3,9847		4,4701
	Синенький платочек		3,9445		4,1398
	Острова свои оберегаем		3,9407		4,4129

	А между прочим осень на дворе		4,0818		4,1676
	Слез не лей …		4,2165		4,4475
	Старый конь		3,9524		4,2452
	Прекрасное небо голубое		4,0479		4,4840
	На реке Сухоне		3,6389		4,3361
	Добрый Филя		3,9008		4,5050
	Оттепель		3,7292		4,4821

Одним из фундаментальнейших понятий математики является понятие меры. В данном случае определение меры сводится к установлению такого диапазона числовых значений Н₁, который определит высокохудожественный или непоэтический текст безотносительно к тому – каким автором он написан. Таким образом можно установить числовую шкалу значений Н₁, с помощью которой можно будет осуществлять безсубъективные оценки поэтических текстов.

В таблице 1 кроме текста Н. Рубцова представлены тексты классиков русской поэзии, поэтому возможно число четыре на указанной шкале будет соответствовать высокохудожественным поэтическим текстам.

При проведении информационных измерений в текстах русского языка, поэтический текст можно считать как набор (множество) букв русского алфавита. Каждый элемент этого множества (каждую букву) можно привести в соответствие с числами натурального ряда в результате чего получим конечное множество, над элементами которого можно производить измерения. Если общее число букв данного текста обозначить через N₂, а через N_i – количество конкретной i-ой буквы, то можно рассчитать

(3)

как частоту появления конкретной буквы в рассматриваемом поэтическом тексте.

При расчете энтропии информации не конкретизируется методика расчета частот, поэтому и к частотам (3) применима формула Шеннона. В данном случае энтропию информации обозначим через Н₂ и ее будем рассчитывать по следующей формуле

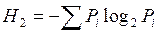(4)

Вернемся снова к тексту «Видения на холме» и для него определим Н₂ по формуле (4).

Таблица 3

а

б

в

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ь

ы

ъ

э

ю

я

1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.

Рис. 1.

2. Запуск программы Microsoft Excel. Результат выполнения представлен на рисунке 2.

Рис. 2.

3. Выбор активного листа.

Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 3. Рис. 3.

4. Автозаполнение - нумерация.

Параметры: - ячейка 1: « A2 »; - ячейка 2: « A3 »;

- конечная ячейка: «A34»; - данные 1: «1»;

- данные 2: «2»; Результат выполнения частично представлен на рисунке 4. Рис. 4.

5. Занесение заголовка в ячейку.

Параметры: - ячейка: A1; - данные: «x».

Результат выполнения представлен на рисунке 5.

Рис. 5.

6. Занесение заголовка в ячейку.

Параметры: - ячейка: B1; - данные: «Буква».

Результат выполнения представлен на рисунке 6.

Рис. 6.

7. Занесение заголовка в ячейку.

Параметры: - ячейка: B2-B34; - данные: «Таблица3».

Результат выполнения частично представлен на рисунке 7. Рис. 7.

8. Подсчёт символов в документе Microsoft Word. Параметры: - символ: «а»; - ячейка MS Excel: «C2». Результат выполнения представлен на рисунке 8. Рис. 8.

Аналогичным, описанному в пункте 8 образом, следует подсчитать количество всех букв алфавита представленного в таблице 3. Результаты подсчёта следует заносить последовательно в ячейки C3-C34. Результат выполнения частично представлен на рисунке 9. Рис. 9.

9. Занесение заголовка в ячейку.

Параметры: - ячейка: C1; - данные: «Кол-во».

Результат выполнения частично представлен на рисунке 10. Рис. 10.

10. Занесение формул в ячейку.

Параметры: - ячейка: С35; - данные: «=СУММ(C2:C34)». Результат выполнения представлен на рисунке 11. Рис. 11.

11. Занесение заголовка в ячейку.

Параметры: - ячейка: B35; - данные: «N₂=».

Результат выполнения частично представлен на рисунке 12. Рис. 12.

12. Занесение заголовка в ячейку.

Параметры: - ячейка: D1; - данные: «Pi».

Результат выполнения представлен на рисунке 13. Рис. 13.

13. Автозаполнение - формула.

Параметры: - ячейка: D2; - данные: «=C2/$C$35» - конечная ячейка: D34. Результат выполнения частично представлен в таблице на рисунке 14. Рис. 14.

14. Автозаполнение - формула.

Параметры: - ячейка: E2; - данные: «=ЕСЛИ(D2=0;0;-D2*LOG(D2;2))» - конечная ячейка: E34. Результат выполнения частично представлен в таблице на рисунке 15. Рис. 15.

15. Занесение заголовка в ячейку.

Параметры: - ячейка: D35; - данные: «H₂=».

Результат выполнения частично представлен на рисунке 16. Рис. 16.

16. Занесение формул в ячейку.

Параметры: - ячейка: E35; - данные: «=СУММ(E2:E34)». Результат выполнения представлен на рисунке 17. Рис. 17.

17. Активизация диапазона ячеек.

Параметры: - диапазон: A1÷D34. Результат выполнения частично представлен на рисунке 18. Рис. 18.

18. Копирование в буфер обмена.

Параметры: - ячейка-источник: «A1÷D34»; - ячейка-цель: «Лист2!A2». Результат выполнения частично представлен на рисунке 19. Рис. 19.

19. Активизация диапазона ячеек.

Параметры: - диапазон: «B1÷D1». Результат выполнения частично представлен на рисунке 20. Рис. 20.

20. Копирование в буфер обмена.

Параметры: - ячейка-источник: «B1÷D1»; - ячейка-цель: «Лист2!B1». Результат выполнения представлен на рисунке 21. Рис. 21.

21. Выбор активного листа.

Параметры: - лист: «Лист2». Результат выполнения представлен на рисунке 22. Рис. 22.

22. Занесение заголовка в ячейку.

Параметры: - ячейка: A1; - данные: «№ буквы».

Результат выполнения частично представлен на рисунке 23. Рис. 23.

23. Активизация диапазона ячеек.

Параметры: - диапазон: «A1÷D34». Результат выполнения частично представлен на рисунке 24. Рис. 24.

24. Копирование в буфер обмена.

Параметры: - ячейка-источник: «A1÷D34»; - ячейка-цель: « E1 ». Результат выполнения представлен на рисунке 25.

Рис. 25.

25. Сортировка данных.

Параметры: - диапазон: «E1÷H34»; - тип: « по возрастанию »; - сортировка: « Pi ». Результат выполнения частично представлен на рисунке 26.

Рис. 26.

26. Активизация диапазона ячеек.

Параметры: - диапазон: «E1÷H1». Результат выполнения частично представлен на рисунке 27. Рис. 27.

27. Копирование в буфер обмена.

Параметры: - ячейка-источник: «E1÷H1»; - ячейка-цель: « I1 ». Результат выполнения представлен на рисунке 28. Рис. 28.

28. Активизация диапазона ячеек.

Параметры: - диапазон: «E2÷E34». Результат выполнения частично представлен на рисунке 29. Рис. 29.

29. Копирование в буфер обмена.

Параметры: - ячейка-источник: «E2÷E34»; - ячейка-цель: « I2 ». Результат выполнения представлен на рисунке 30. Рис. 30.

30. Активизация диапазона ячеек.

Параметры: - диапазон: «F2÷H2». Результат выполнения частично представлен на рисунке 31. Рис. 31.

31. Копирование в буфер обмена.

Параметры: - ячейка-источник: «F2÷H2»; - ячейка-цель: « J34 ». Результат выполнения представлен на рисунке 32. Рис. 32.

32. Активизация диапазона ячеек.

Параметры: - диапазон: «F3÷H3». Результат выполнения частично представлен на рисунке 33. Рис. 33.

33. Копирование в буфер обмена.

Параметры: - ячейка-источник: «F3÷H3»; - ячейка-цель: « J2 ». Результат выполнения представлен на рисунке 34. Рис. 34.

Аналогично повторим шаги 30-33 для оставшихся диапазонов с F4÷H4 до F34÷H34. Вставку скопированных диапазонов следует производить в ячейки c J4 до J34 соответственно. Результат выполнения частично представлен на рисунке 35.

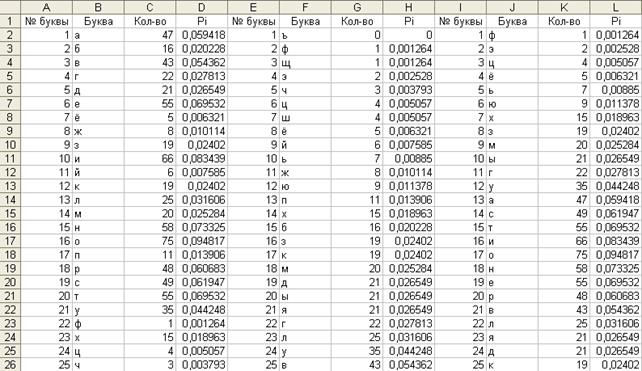
Рис. 35.

34. Построение диаграммы.

Параметры: - диапазон данных: « L2÷L34 »; - диапазон подписей: « J2÷J34 »; - тип: « гистограмма »; - вид: « обычная гистограмма »; - название оси Х: « буква »; - название оси Y: « Pi »; - размещение: «в отдельном листе ». Результат выполнения представлен на рисунке 36.

Рис. 36. Гистограмма нормального распределения частот.

Гистограмма нормального распределения частот иллюстрирует процесс группирования частот относительно максимальной частоты. Характер такой группировки может также характеризовать индивидуальность текста.

Действительно, гистограмма на рис. 36 представляет распределение частот букв русского алфавита для текста «Видения на холме». Однако из сочетания букв образуются такие составляющие слова, как слоги и корни. Поэтому представляется реальным создание определенного алгоритма, по которому из частотного распределения букв можно определить частоты появления определенных слогов и корней.

В таблице 2 представлены рассчитанные по вышеуказанной технологии величины Н₂ для различных текстов Н. Рубцова. Диапазон изменения чисел Н₂ оказался меньшим по сравнению с диапазоном Н₁. Однако оказались такие тексты, для которых числовые значения Н₁ и Н₂ близки. Например, текст «Видения на холме». Возможно, этот факт служит еще одним доказательством того, что число четыре на числовой шкале соответствует высоко художественным текстам.

Дата добавления: 2015-06-26