Парная линейная регрессионная модель

Подгонка кривой.

Пусть есть результаты наблюдений 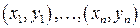переменных и , которые можно изобразить в виде точек в декартовой системе координат:

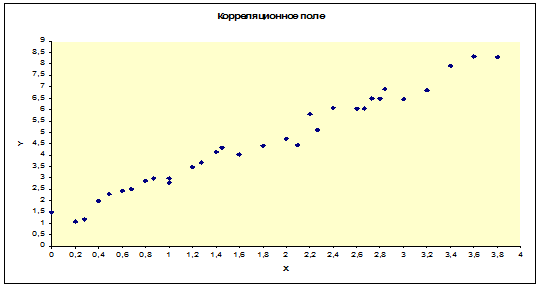
Получаемое таким образом изображение получило название диаграммы рассеяния или корреляционного поля наблюдений.

Нашей задачей является подобрать («подогнать») функцию 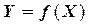из параметрического семейства функций 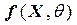, «наилучшим» способом описывающую зависимость от . По виду диаграммы рассеивания видно, что примером параметрического семейства может служить семейство линейных функций .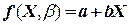

В модели парной линейной регрессии зависимость между переменным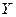и и представляется в виде

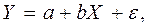
где - случайная ошибка модели. Постоянные — неизвестные параметры модели.

Природа случайной ошибки:

· попытка учесть влияние на зависимую переменную других факторов,

· возможную нелинейность модели,

· наличие ошибок измерения.

Выбор линейной модели обычно обуславливается:

· содержательными соображениями,

· геометрическими соображениями (использование корреляционного поля наблюдений),

· вычисление выборочного коэффициента корреляции Пирсона

Встает задача нахождения оценок неизвестных параметров 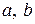по результатам наблюдений . Точечные оценки неизвестных параметров , найденные по методу наименьших квадратов имеют вид:

.

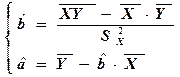Оценку функции регрессии (эмпирическую регрессию, выборочную регрессию, уравнение прямой регрессии по ) определяет соотношение:

.

Продолжение примера 1.

Построим поле корреляции и определим по нему характер зависимости.

На основании построенного поля корреляции можно сделать вывод о том, что для описания зависимости между X и Y можно воспользоваться уравнением прямой, поскольку точки-наблюдения располагаются близко вдоль некоторой предполагаемой прямой.

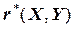Этот факт можно подтвердить или опровергнуть, вычислив значение коэффициента корреляции Пирсона: (см. пример 1). Значение близко к единице. Следовательно, мы имеем достаточно сильную линейную зависимость между X и Y, что подтверждает наше предположение о том, что для описания зависимости между X и Y можно использовать модель:

Точечные оценки неизвестных параметров равны:

Таким образом, уравнение регрессии принимает вид

Подтвердим графически правдоподобность полученного результата. Построим прямую, задаваемую уравнением, на поле корреляции.

Пусть 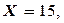тогда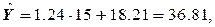

и 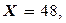тогда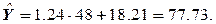

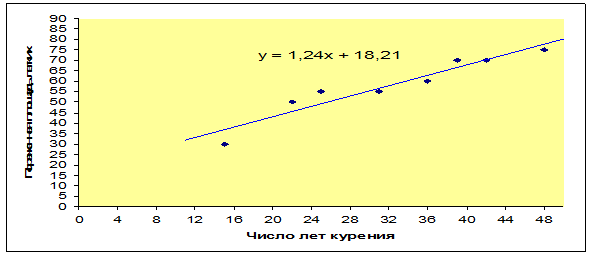
Давая содержательную интерпретацию полученным коэффициентам уравнения регрессии, можно заключить, что каждый дополнительный год курения увеличивает площадь пораженной части легких у людей, заболевших эмфиземой, в среднем на 1,24%.

Дата добавления: 2015-06-26