Элементы теории вероятностей

Решение.

Пример.

В почтовом отделении продают открытки 10 сортов. Сколькими способами можно купить в нем: а) 12 открыток? б) 8 открыток? в) 8 различных открыток?

а)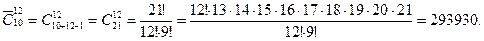

б)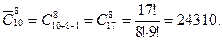

в)

Домашнее задание.

1. У филателиста есть 8 различных марок на космическую тему и 10 различных марок на спортивную тему. Сколькими способами он сможет наклеить 3 марки одного вида и 3 марки второго вида в альбом на 6 пронумерованных мест?

2. В лаборатории работают 8 физиков и 10 химиков. Надо создать рабочие группы по трем темам. В первую группу должны войти 4 физика, во вторую 5 химиков, а третья должна состоять из 3 человека которые могут быть как физиками, так и химиками. Сколькими способами можно создать такие группы.

3. Доказать, что 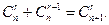(правило Паскаля).

Вариант 1.

1. Ребенок, играя десятью кубиками, на которых написаны буквы М, М, Т, Т, А, А, А, К, И, Е, сложил слово «МАТЕМАТИКА». Можно ли считать, что ребенок грамотный?

2. Из колоды карт наудачу берутся четыре карты. Найти вероятность появления хотя бы одного короля.

3. В трех ящиках находится по десять деталей: в первом 8, во втором 7 и в третьем 9 стандартных. Из каждого ящика наугад вынимают по одной детали. Какова вероятность того, что две из трех извлеченных деталей стандартные?

4. В урне пять белых и четыре черных шара. Из урны извлекают по одному шару без возвращения в урну. Найти вероятность того, что при первом извлечении появится белый, а при втором – черный шар.

Вариант 2.

1. С площади уезжают четыре автомобиля, причем каждый из них может с равной вероятностью поехать по любой из четырех улиц, начинающихся от этой площади. Какова вероятность того, что:

а) все авто поедут по одной и той же улице?

b) по каждой из улиц поедет автомобиль?

2. Из колоды карт наугад берутся четыре карты. Найти вероятность появления хотя бы одного туза.

3. Найти вероятность совместного появления двух гербов и цифры при одном бросании трех монет.

4. У сборщика имеется три конусных и семь эллиптических валиков. Сборщик наугад взял один валик, затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический.

Вариант 3.

1. Для уменьшения общего количества игр на соревнованиях 16 волейбольных команд разбиты на две подгруппы (по 8 команд в каждой). Какова вероятность того, что две наиболее сильные команды окажутся:

a) в разных подгруппах?

b) в одной подгруппе?

2. Из колоды карт наугад берутся четыре карты. Найти вероятность появления хотя бы одной дамы.

3. Найти вероятность того, что при бросании двух игральных костей сумма выпавших очков будет равна шести.

4. В урне семь белых и три черных шара. Наугад извлекается сначала один шар без возввращения, затем второй. Найти вероятность того, что вторым будет извлечен черный шар.

Вариант 4.

1. Вы справляете свой день рождения с 10 друзьями. Какова вероятность того, что хотя бы у двух из них дни рождения совпадают? (годы рождения могут не совпадать)? Какова вероятность того, что дни рождения ваших друзей придутся на разные месяцы года?

2. Из колоды карт наугад берутся четыре карты. Найти вероятность появления хотя бы одного валета.

3. Имеется два ящика, содержащие по 10 деталей: в первом 7, во втором 8 стандартных. Из каждого ящика наугад вынимают по одной детали. Какова вероятность того, что обе детали будут разными по качеству?

4. В урне семь белых и три черных шара. Наугад извлекается сначала один шар без возвращения в урну, затем второй. Какова вероятность того, что будут извлечены два белых шара.

Вариант 5

1. Семь студентов условились ехать в одой электричке, но не договорились о вагоне. Какова вероятность того, что ни один из них не встретится с другим, если в составе электропоезда 7 вагонов.

2. В ящике имеется 12 деталей, из которых 6 стандартных. Найти вероятность того, что среди четырех наугад извлеченных деталей есть хотя бы одна стандартная.

3. Вероятность попадания в цель при стрельбе из трех орудий такова: Р₁ = 0, 7; Р₂ = 0, 8; Р₃ = 0, 9. Найти вероятность поражения цели при одном залпе из всех орудий.

4. Для некоторой местности среднее число пасмурных дней в июле равно шести. Найти вероятность того, что первого и второго июля будет ясная погода.

Вариант 6

1. Игральная кость бросается три раза. Какова вероятность того, что

a) ни разу не выпало пять очков;

b) каждый раз выпадало одно и тоже число очков;

c) все числа выпавших очков оказались различными?

2. В ящике имеется 12 деталей, из которых 7 стандартных. Найти вероятность того, что среди четырех наугад извлеченных деталей есть хотя бы одна нестандартная.

3. Два стрелка стреляют по мишени. Вероятность поражения при одном выстреле для первого стрелка 0, 7, для второго – 0, 8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

4. На практических занятиях в студенческой группе присутствуют семь юношей и восемь девушек. По номерам из списка наугад отобраны трое, для работы у доски. Найти вероятность того, что все отобранные лица окажутся юношами.

Вариант 7

1. В лифт пятиэтажного дома на I-ом этаже вошли три человека. Каждый из них с одинаковой вероятностью, выходит на любом из этажей, начиная со второго. Какова вероятность того, что

a) на каждом этаже выйдет не более одного пассажира;

b) ни один из пассажиров не выйдет на втором этаже;

c) все пассажиры выйдут на одном и том же этаже?

2. Стрелок стреляет по мишени, разделенной на три области. Вероятность попадания в первую область 0, 45, во вторую – 0, 35. Найти вероятность того, что при двух выстрелах стрелок попадет либо в первую, либо во вторую область.

3. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятности надежности сигнализаторов равны 0, 95 и 0, 9. Найти вероятность того, что при аварии сработает только один сигнализатор.

4. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что из трех вопросов, предложенных ему экзаменатором, студент знает только два вопроса.

Вариант 8

1. Вы останавливаете на улице наудачу трех человек и выясняете, в какой день недели они родились. Какова вероятность того, что

a) все родились в среду;

b) ни один не родился в субботу;

c) все родились в различные дни недели?

2. В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша для владельца одного лотерейного билета?

3. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0, 38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0, 8.

4. В урне находятся пять белых, четыре черных и три синих шара. Из урны извлекают по одному шару без возвращения. Какова вероятность того, что при первом испытании появится белый шар, при втором черный, при третьем синий.

Вариант 9

1. Найти вероятность того, что последняя цифра квадрата или четвертой степени произвольного целого числа окажется единицей.

2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди трех наугад извлеченных деталей есть хотя бы одна стандартная.

3. Вероятность поражения цели при одном выстреле для одного стрелка 0, 6, для второго – 0, 7. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

4. В урне имеется пять шаров с номерами от 1 до 5. Наугад по одному извлекают три шара без возвращения. Найти вероятность того, что последовательно появятся шары с номерами 1, 4, 5.

Вариант 10

1. Наудачу набирается семизначный телефонный номер. Какова вероятность того, что

a) все цифры номера различны;

b) номер начинается с цифры 2;

c) все цифры номера нечетные?

2. В ящике 10 деталей, среди которых три стандартные. Найти вероятность того, что среди шести наугад отобранных деталей не более двух нестандартных.

3. ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0, 9. Найти вероятность того, что из трех проверенных изделий одно стандартное и два нестандартных.

4. В урне имеется пять шаров с номерами от 1 до 5. Наугад по одному извлекают три шара без возвращения. Найти вероятность того, что извлеченные шары будут иметь номера 1, 2, 3 независимо от того, в какой последовательности они появились.

Раздел II

Дата добавления: 2015-06-26