Кинематики и динамики

ФОРМУЛЫ

АЗОТСОДЕРЖАЩИЕ ГЕТЕРОЦИКЛЫ.

Названия некоторых органических веществ.

Формула	Систематическое название и пояснение
	Пиридин, азотсодержащее соединение с щестичленным циклом, содержащий один гетероатом (азот)
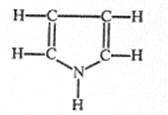
	Пиррол, азотсодержащее соединение с пятичленным циклом, содержащий один гетероатом (азот)
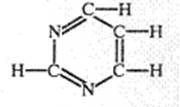
	Пиримидин, азотсодержащее соединение с щестичленным циклом, содержащий два гетероатома (азота)
	Пурин, сложная гетероциклическая система, состоящая из двух гетороциклов
Тимин Цитозин	Тимин и цитозин, производные пиримидина
Аденин Гуанин	Аденин и гуанин, производные пурина

ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ	ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Линейная координата х, Перемещение	Угловая координата (угол) Аксиальный вектор
Линейная скорость ,	Угловая скорость ,
Линейное ускорение	Угловое ускорение
Сила	Момент силы
Масса m	Момент инерции
Импульс (количество движения)	Момент импульса ;
Работа (механическая)	Работ вращения Работа в плоскости xy
Мощность (мгновенная)	Мощность (мгновенная)
Кинетическая энергия поступательного движения	Кинетическая энергия вращения
Основное уравнение (2-й закон Ньютона) (при m=const )	Основное уравнение (2-й закон Ньютона) (при J =const )
Приближение материальной точки или приближение абсолютно твёрдого тела, совершающего поступательное движение, т. е. движение, при котором любая прямая, проведённая между двумя точками тела, остаётся параллельной сама себе.	Приближение абсолютно твёрдого тела – тела, расстояния между любыми частями которого сохраняются.

При сопоставлении формул кинематики и динамики для поступательного и вращательного движений примечательным является то обстоятельство, что формулы для двух типов движений похожи и, более того, формулы для вращательного движения легко получаются из формул для поступательного движения соответствующими заменами. Так, масса m, параметр при описании поступательного движения, при переходе к вращательному движению должна быть заменeна на момент инерции J, аналогичный по смыслу параметр при описании вращательного движения. Соответственно, сила меняется на момент сил , импульс - на момент импульса , линейная координата - на угловую координату и т. д. Так происходит потому, что вращательное движение, по сути, - это согласованный набор микроскопических (точнее, бесконечно малых) поступательных перемещений отдельных (тоже бесконечно малых) частей абсолютно твёрдого тела. Ну, а физика поступательного движения в любом случае описывается уравнениями Ньютона.

Прямая связь между поступательным и вращательным движениями отражена в кинематических формулах, связывающих параметры этих двух типов движений:

- связь между длиной дуги окружности и углом (фактически определение радианной меры угла) ;

- связь между линейной и угловой скоростью ();

- связь между тангенциальной составляющей линейного ускорения и угловым ускорением ();

- связь между нормальной составляющей линейного ускорения и угловой скоростью ().

Последние две строчки поясняются следующими выкладками:

.

Напомним, также, что:

- - аксиальные векторы, т. е. векторы параллельные оси вращения;

- вектор линейной скорости всегда касателен к траектории, значит ;

- вектор перпендикулярен оси вращения и «смотрит» от оси;

- вектор тангенциального ускорения параллелен линейной скорости ;

- вектор нормального ускорения перпендикулярен линейной скорости и параллелен вектору (но «смотрит» к оси вращения);

- и ;

- циклическая частота (угловая скорость) связана с частотой вращения , принятой в технике, соотношением .

Профессор, д. т. н. Гребёнкин М. Ф.

Дата добавления: 2015-06-04