
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Остойчивость формы и остойчивость нагрузки
|
|
|
|
Рассмотрение этого вопроса позволяет установить природу остойчивости, выяснить физические причины возникновения восстанавливающего момента при наклонениях судна. В соответствии с метацентрическими формулами остойчивости (углы Θ и Ψ выражены в радианах):
mΘ = γV h Θ = γV (r – α) Θ = γV r Θ – γV α Θ;
МΨ = γV Н Ψ = γV (R – α) Ψ = γV R Ψ – γV α Ψ.
Таким образом, восстанавливающие моменты mΘ, МΨ и плечи статической остойчивости lΘ, l Ψ представляют собой алгебраическую сумму их составляющих:
mΘ = mф + mн; МΨ = Мф + Мн;
lΘ = lфΘ + lнΘ; l Ψ = l фΨ + l нΨ,
где моменты
mф = γV r Θ;
Мф= γV R Ψ,
принято называть моментами остойчивости формы, моменты
mн = – γV α Θ;
Мн = – γV α Ψ,
моментами остойчивости нагрузки, а плечи
lфΘ = mф / γV;
lфΨ = Мф / γV,
поперечными и продольными плечами остойчивости формы, плечи
lнΘ = – mн / γV;
lнΨ = – Мн / γV,
поперечными и продольными плечами остойчивости нагрузки.
Так как: r = 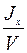 ; R =
; R = 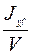 ; α = zg – zc,
; α = zg – zc,
где Jx и Jyf – момент инерции площади ватерлинии относительно поперечной и продольной центральной оси соответственно, то моменты формы и нагрузки можно представить в виде:
mф = γ Jx Θ, Мф= γ Jyf Ψ;
mн = – γV (zg – zc) Θ, Мн = – γV(zg – zc) Ψ.
По своей физической природе момент остойчивости формы всегда действует в сторону, противоположную наклонению судна, и, следовательно, всегда обеспечивает остойчивость. Он вычисляется через момент инерции площади ватерлинии относительно оси наклонения. Именно остойчивость формы предопределяет значительно большую продольную остойчивость по сравнению с поперечной т.к. Jyf» Jx.
Момент остойчивости нагрузки из-за положения ЦТ выше ЦВ α = (zg – zc) > 0, всегда уменьшает остойчивость судна и по существу она обеспечивается только остойчивостью формы.
Можно предположить, что в случае отсутствия ватерлинии, например, у подводной лодки в подводном положении, момент формы отсутствует (Jx = 0). В подводном положении подводная лодка за счет балластировки специальных цистерн, имеет положение ЦТ ниже ЦВ, в результате ее остойчивость обеспечивается остойчивостью нагрузки.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 415; Нарушение авторских прав?; Мы поможем в написании вашей работы!