
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика
|
|
|
|
1.Динамика мәселелері. Динамикада материалық нүкте мен материалық дененің қозғалыстары оларды болдыратын физикалық себептермен, яғни күштермен тығыз байланысты қарастырады. Денеге түсірілген күштер мен олардың әсерінен болатын қозғалыс арасындағы тәуелділікті зерттеу. Сөйтіп қозғалыстың жалпы заңдылығын табу мәлелелері қарастырылады.
Материялық нүкте деп қозғалыстың берілген жаңдайларында өлшемдерін ескермеуге болатын денені айтамыз.
Дененің материя мөлшерінің өлшемі ретінде алынатын, P/g=const=m- қатынаспен анықталатын, шаманы дененің ауырлық (гравитациялық) массасы дейді.
Материялық денелердің механикалық өзара әсерлесуінің өлшемі ретінде алынатын шаманы механикада күш деп атайды. Күш-векторлық шама. 1-шамасына, 2-бағытына, 3-түсу нүктесіне тәуелді.Халықаралық жүйеде 1Н, ал бірліктердің техникалық жүйесінде 1кГ.
6. Кедергі жылдамдыққа үлесті (пропорционал) болғандағы кедергісіз ортада нүктенің еріксіз (мәжбүрлі) тербелісі. Резонанс жағдайы.
R=0 b=0
X=asin(nt+E)+P\(n2-p2)sin[(pt+∂)-α]
A= 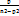 A мәжбүрлі тербелістер амплитудасы
A мәжбүрлі тербелістер амплитудасы
Егер мәжбүр етуші Q күшінің жиілігі және өзіндік тербелістердің жиілігі өзара теңесіп кетсе, яғни p=n онда А>∞ болады, осы кезде резонанс деп аталатын құбылыс пайда болады.
7. Материалық нүктенің қозғалыс мөлшері. Күштің элементар және толық импульсі. Қозғалыс мөлшерінің өзгеруі туралы теорема.
Материялық нүктенің м массасы мен V жылдамдығының көбейтіндісіне тең q=mv векторын оның қозғалыс мөлшері дейміз. Q векторы нүктеге түсірілген Ғ күші әсерінен уақыт өткен сайын өзгеріп отырады.
m 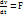 немесе
немесе 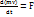 . Теңдеудің екі жағында dt-ға көбейтеміз.
. Теңдеудің екі жағында dt-ға көбейтеміз.
D(mv)=Fdt. Fdt көбейтіндісін күштің элементар импульсі деп атайды. Теорема түрінде былай: материялық нүктенің қозғалыс мөлшерінің дифференциалы күшінің импульсына тең. Уақыт t=t0 болған нүкте жылдамдығы v=v0 болады дейік. Теңдіктің сол жағын Vдан V0 дейінгі шектерде, ал оң жағынан t0 ден t ға дейінгі шектерді интегралды алайық:
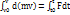 mv-mv0=
mv-mv0=  (1)
(1)
Элементар импульстерден t=t0 уақыт аралығында алынған интегралмен анықталатын S векторын күштің сол уақыт аралығындағы импульсі деп атайды.
S=  Күш импульсінің координаттар өстеріндегі проекциялары мынадай теңдіктермен анықталады.
Күш импульсінің координаттар өстеріндегі проекциялары мынадай теңдіктермен анықталады.
Sx= 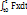 Sy=
Sy= 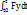 Sz=
Sz= 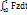 mv-mv0 = S (2)
mv-mv0 = S (2)
1 және 2 теңдіктері материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема: қандай да уақыт аралығындағы нүктенің қозғалыс мөлшерлерінің өзгеруі сол уақыт аралығындағы күш импульсіне тең.
Теореманың координаттық өстерге проекциясы былай айтылады: нүктенің өозғалыс мөлшерінің берілген өстегі проекциясының қандайда бір уақыт аралығындағы өзгеруә сол уақыт аралығындағы күш импульсінің осы өстегі проекциясына тең.
8. Материалық нүктенің кинетикалық моменті. Материалық нүктенің кинетикалық моментінің өзгеруі туралы теорема.
Материялық нүктенің қозғалыс мөлшерінің қандайда бір центрге қатысты алынған моментін оның сол центрге қатысты кинетикалық моменті дейді. О центріне қатысты алынған кинет.момент К0 әрпімен белгілейік. Сонда ол, К0= r×mv немесе K0= M0(mv) өрнекпен беріледі. Кинетикалық момент күш әсерінен уақыт өткен сайын өзгеріп отырады. Теңдеудің екі жағын да нүктенің r радиус векторына векторлық түрде көбейтеміз. r×m 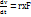 (1). Бұл теңдеудің сол жағындағы векторлық көбейтіндіні түрлендірейік. r×m
(1). Бұл теңдеудің сол жағындағы векторлық көбейтіндіні түрлендірейік. r×m  2ші теңдеудің сол жағын 1ші теңдеуге қоямыз.
2ші теңдеудің сол жағын 1ші теңдеуге қоямыз.  . Осы теңдің материялық нүкте қозғалыс мөлшері моментінің өзгеруі туралы немесе басқаша айтқанда, нүктенің кнетикалық моментінің өзгеруі туралы теореманы өрнектейді. Жоғарыда берілген материялық нүктенің кинетикалық моменті деген анықтаманы қолдану арқылы 3ші теңдеуді былай жазамыз.
. Осы теңдің материялық нүкте қозғалыс мөлшері моментінің өзгеруі туралы немесе басқаша айтқанда, нүктенің кнетикалық моментінің өзгеруі туралы теореманы өрнектейді. Жоғарыда берілген материялық нүктенің кинетикалық моменті деген анықтаманы қолдану арқылы 3ші теңдеуді былай жазамыз.  (4). 3ші және 4ші тендеумен орнектелетін теорема былай айтылады: қандайда бір центрге қатысты алынған нүкте кинетикалық моментінің уақыт бойынша туындысы сол центрге қатысты күш моментіне тең. Үш өске проекцияласақ:
(4). 3ші және 4ші тендеумен орнектелетін теорема былай айтылады: қандайда бір центрге қатысты алынған нүкте кинетикалық моментінің уақыт бойынша туындысы сол центрге қатысты күш моментіне тең. Үш өске проекцияласақ:
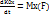
 (5). 5ші теңдеу кин.момент өзгеруін сипаттайды: координаттар өстеріне қатысты алынған нүкте кинетикалық моменттерінің уақыт бойынша туындылары сол өстерге қатысты алынған күш моменттеріне тең.
(5). 5ші теңдеу кин.момент өзгеруін сипаттайды: координаттар өстеріне қатысты алынған нүкте кинетикалық моменттерінің уақыт бойынша туындылары сол өстерге қатысты алынған күш моменттеріне тең.
9. Материалық нүктенің кинетикалық энергиясы. Материалық нүктенің кинетикалық энергиясының өзгеруі туралы теорема.
Нүктенің кинетикалыө жнергиясы деп оның массасы мен жылдамдығының квадратының көбейтіндісінің жартысына тең болатын скаляр шаманы айтады. Егер нүктенің кинетикалық энергиясын Т деп алсақ, формуласы былай: T= 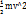 (1). Күш әсерінен нүкте жылдамдығы өзгереді. Сол себепті кинет.энергия да уақыт өткен сайын өзгеріп отырады. 1ші теңдеу екі жағында drға элементар орын ауыстыруға көбейтейік.
(1). Күш әсерінен нүкте жылдамдығы өзгереді. Сол себепті кинет.энергия да уақыт өткен сайын өзгеріп отырады. 1ші теңдеу екі жағында drға элементар орын ауыстыруға көбейтейік.
m 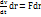 . Бұл теңдеудің сол жағын түрлендірейік: m
. Бұл теңдеудің сол жағын түрлендірейік: m  = mdv×v=d(
= mdv×v=d(
Нәтижесінде d( =Fdr. Dr элементар орын ауыстыруға күштің элементар жұмысы деп атайды. Элементар жұмысты d’A деп белгілейміз. d’A=Fdr. Кинет.энергия мен элементар жұмыс белгілеулерін пайдаланып dT=d’A. Материялық нүкте өз траекториясын АВ қисығы бойымен М0М1жолын жүреді. Жылдамдығы V0 ден V1 ге –өзгереді. М0M1 жолындағы күштің толық жұмысы А қисықтың М0M1 доғасы бойындағы элементар жұмыстарынан алынған қисық сызықты интегралға тең: A=
=Fdr. Dr элементар орын ауыстыруға күштің элементар жұмысы деп атайды. Элементар жұмысты d’A деп белгілейміз. d’A=Fdr. Кинет.энергия мен элементар жұмыс белгілеулерін пайдаланып dT=d’A. Материялық нүкте өз траекториясын АВ қисығы бойымен М0М1жолын жүреді. Жылдамдығы V0 ден V1 ге –өзгереді. М0M1 жолындағы күштің толық жұмысы А қисықтың М0M1 доғасы бойындағы элементар жұмыстарынан алынған қисық сызықты интегралға тең: A=  (2)
(2)
Мат.нүктенің бастапқы орындағы кин.энергиясын T0 деп, ал соңғы орындағысын T1 белгілесек және күш жұмысын 2ші формуламен өрнектесек: T1 – T0 =A. Нүктенің қандай да бір орын ауыстыруындағы кинетикалық энергиясының өзгеруі сол орын ауыстыырудағы оған әсер етуші күштің жұмысына тең.
10. Механикалық жүйе динамикасы. Жүйе массасы; масса ортасы (центрі). Күштерді топқа бөлу, ішкі күштер ерекшелігі.
Механикалық нүктелердің механикалық жүйесі деп қозғалыстары өзара тәуелді болып келетін материялық нүктелер жиынтғын айтады. Егер қозғалыс кезінде жүйедегі нүктелердің бір бірінен ара қашықтықтары өзгермей сақталатын болса, онда бұл жүйені өзгермейтін механикалық жүйе дейміз. Абсолют қатты дене өзгермейтін мех.жүйе ретінде қарастыралады. Берілген мех.жүйе сыртқы күштері деп осы жүйе құрамына енбейтін сыртқы жүйе нүктелерінежасайтын әсерлерінен туатын күштерді айтамыз F деп белгілейміз. Берілген мех.жүйе нүктелерінің арасында болатын өзара әсерлесу күштерін ішкі күштер дейміз. Ішкі күштер берілген жүйе нүктелерінің арасындағы өзара әсер етуші күштер болғандықтан оларға Ньютонның 3-ші заңын қолдана аламыз. Осыдан жүйенің қос қостан алынған ішкі күштер шама жағынан тең,бір түзу бойымен бір біріне қарама қарсы бағытталған күштер жүйесінің бас векторы және кез келген центрге қатысты алынған, олардың бас моменті үнемі нолге тең.
Ri=∑Fk =0 M0i=∑M0(Fk)=0. Бұл күш маңызды қасиет болып табылады.
Мех.жүйе массасы деп ондағы нүктелер массаларының қосындысына тең болатын шаманы айтамыз.
M=∑mk
Мех.жүйе массаларының центрі деп радиус векторы r= 
Коор.форы: Хс= 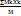 Yс=
Yс=  Zс=
Zс= 
Кейде бұл нүктені мех.жүйенің инерциялар центрі д.ат.
Rk = 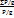 =
= 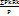
11. Механикалық жүйе қозғалысының дифференциалдық теңдеулері. Жүйенің масса ортасының қозғалу теоремасы. Масса ортасының қозғалысын сақтау теоремасы.
Еркін мех.жүйе  Коор.түрі:
Коор.түрі:
mkXk=Fkxe+Fkxi
myYk=Fkye+Fkyi (k=1,n)
mkZk=Fkze+Fkzi
Еркін емес мех.жүйе: 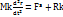
mYk=Fkx+Rkx
mYk=Fky+Rky (k=1,n)
mY=Fkz+Rkz
 дәлелдеу үшін: теңдеулердің барлығын бір біріне қосамыз: сонда:
дәлелдеу үшін: теңдеулердің барлығын бір біріне қосамыз: сонда:
∑m 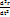 = ∑Fke + ∑Fki M
= ∑Fke + ∑Fki M 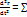 Fke немесе Ma=Re
Fke немесе Ma=Re
Мех.жүйе массалар центрі материялық нүкте сияқты қозғалады. Бұл нүктенің массасы тұтас жүйенің массасына тең, ал оған әсер етуші күш мех.жүйенің сыртқы күштерінің бас векторына тең болады. Коорд.остерге проекциялаймыз: MXc=Rxe MYc=Rye MZc=Rze
Xc. Yc Zc массалар центрінің үдеуінің коор.остеріндегң проекциялары
12. Материалдық жүйенің қозғалыс мөлшері. Күштің лездік және толық импульсі. Механикалық жүйе қозғалыс мөлшерінің өзгеру теоремасы. Сақталу теоремасы.
Мех.жүйенің қозғалыс мөлшері деп, ондағы барлық материялық нүк.қозғалыс мөлшерлерінің геометриялық қосындысына тең болатын Q векторын айтады7
Q=∑mkvk/ Коор.остеріндегі проек Qx=∑mkvkx Qy=∑mkvky Qz=∑mkvkz
Жүйенің қозғалыс мөлшері мен масс.центр жылдамдығы арасында тәуелділік бар, осы теңдеуден екі жағынан да уақыт бойынша туынды табамыз:
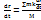 =
= 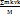 Осы теңдіктен мынау шығады: Q=Mvc
Осы теңдіктен мынау шығады: Q=Mvc
Жүйенің қозғалысы кезінде оның Q қозғалысы мөлшері күштердің әсерінен уақыт өткен сайын өзгеріп отырады. Механикалық жүйенің қозғалыс мөлшерінен уақыт бойынша алынған туынды жүйеге әсер етуші барлық сыртқы күштердің бас векторына тең.
∑m 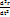 = ∑Fke + ∑Fki
= ∑Fke + ∑Fki
∑m 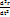 =
=  (∑mkvk)=
(∑mkvk)= 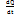
 = ∑Fk немесе
= ∑Fk немесе  = Re
= Re
 =
= 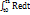 Q1-Q0=
Q1-Q0= 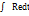
Q-Q=S
Жүйенің қозғалыс мөлшерінің қандай да бір уақыт аралығындағы өзгеруі, сыртқы күштердің бас векторының сол уақыт аралығындағы импульсіне тең.
Q1x-Q0x=Sxe Q1y-Q0y=Sye Q1z-Q0z=Sze
Q=const егер сыртқы күштердің бас векторы Re=0 болып келсе, онда мех.жүйенің Q векторы қозғалыс кезінде өзінің шамасы мен бағыты өзгертпей сақтайды.
13.Механикалық жүйенің қозғалыс мөлшері.
Берілген механикалык жуйе n материялық нүктелерден құралады. Жүйенің массасы mk және жылдамдығы vk тең М нуктесінің қозғалыс мөлшері qk=mkvk векторымен беріледі.Жүйедегі нүктелер қозгалыс мөлшері qk векторларының бас векторы механикалық жүйенің қозғалыс мөлшері ретінде алынады.Басқаша айтқанда,механикалық жуйенің қозғалыс мөлшері деп,ондағы барлық материялық нүктелердің қозғалыс мөлшерлерінің геометриялық қосындысына тең болатын Q векторын айтамыз. Q=∑mkvk
Механикалық жүйенің қозғалу мөлшер моментінің өзгеру теоремасы. Жүйенің қозғалысы кезінде оның Q қозғалысы мөлшері күштердің әсерінен уақыт өткен сайын өзгеріп отырады. Q векторы өзгеруінің жүйеге әсер етуші куштерге тәуелділігі мынадай теоремамен анықталады:механикалық жүйенің қозғалыс мөлшерінен уақыт бойынша алынған туынды жүйеге әсер етуші барлық сыртқы күштердің бас векторына тең.
Сақталу заңдылығы.
Егер механикалық жүйеге әсер ететін сыртқы күштерінің бас векторы нөлге тең болып келетін болса Rе=0,онда теорема өрнегі теңдеуінен мынадай теңдік шығады: Q=const=Qo, мұндағы, Qo жүйенің қозғалыс мөлшерінің бастапқы мәні. Теңдік қозғалыс мөлшерінің сақталу заңы былай айтылады:егер сыртқы күштердің бас векторы Rе=0 болып келсе,онда механикалық жүйенің Q векторы қозғалыс кезінде өзінің шамасы мен бағытын өзгертпей сақтайды.
14.Күштің элементарлық және толық жұмысы. Қуат.
Элементар жұмыстың векторлардың скалярлық көбейтіндісі түрінде алынған өрнегінен сол векторлардың проекциялары арқылы жазылуына көшуге болады. d’A = Fxdx + Fydy + Fzdz Күштің элементар жұмысын есептеу үшін тағы бір формула: d’A =Fdr=Fvdt Элементар жұмыстың әр түрлі өрнегіне сәйкес,күштің толық жұмысы да әр түрлі формулалармен сипатталады: A=  xdx+Fydy+Fzdz, A=
xdx+Fydy+Fzdz, A=  cosα)dS, A=
cosα)dS, A=  vdt Жұмыс өлшемінің бірлігі үшін 1 Джоуль алынады.(1ДЖ=1Нм),ал техникалык жуйеде – 1кГм(1кГм=9,81). Уақыт бірлігіне қатысты алынған жұмыс қуат деп аталынады.Қуатты N деп алсақ,онда оны мына формуламен анықтаймыз: N=
vdt Жұмыс өлшемінің бірлігі үшін 1 Джоуль алынады.(1ДЖ=1Нм),ал техникалык жуйеде – 1кГм(1кГм=9,81). Уақыт бірлігіне қатысты алынған жұмыс қуат деп аталынады.Қуатты N деп алсақ,онда оны мына формуламен анықтаймыз: N= 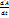 . Қуат бірлігі үшін 1ватт(1Вт=1Дж/с)алынады. Жұмысты есептеу мысалы. Салмағы 2m жүкті горизонтпен 300 бұрыш құратын көлбеу жазықтықтың бойымен 5м биіктікке көтеру үшін жұмсалатын ең аз жұмысты анықтау қажет.Уйкеліс коэффициенті 0.5-ке тең.Жүкке түсірілген күштер:оның салмақ күші – P,үйкеліс күші – Fүйк , көлбеу жазықтықтың нормаль реакция күші – N. Шешуі: жүкке түсірілген күштер жұмыстарының қосындысы: ∑Аi=A(P)+A(Fүйк)=-mgh-fmghctgα=-mgh(1+fctgα)=-2000*9.81*5(1+0.5*1.732)= -183000Дж. Модулін қабылдаймыз. А=183кДж
. Қуат бірлігі үшін 1ватт(1Вт=1Дж/с)алынады. Жұмысты есептеу мысалы. Салмағы 2m жүкті горизонтпен 300 бұрыш құратын көлбеу жазықтықтың бойымен 5м биіктікке көтеру үшін жұмсалатын ең аз жұмысты анықтау қажет.Уйкеліс коэффициенті 0.5-ке тең.Жүкке түсірілген күштер:оның салмақ күші – P,үйкеліс күші – Fүйк , көлбеу жазықтықтың нормаль реакция күші – N. Шешуі: жүкке түсірілген күштер жұмыстарының қосындысы: ∑Аi=A(P)+A(Fүйк)=-mgh-fmghctgα=-mgh(1+fctgα)=-2000*9.81*5(1+0.5*1.732)= -183000Дж. Модулін қабылдаймыз. А=183кДж
15. Кинетика-қ момент-ң өгеруі туралы теореманы қатты дене-ң айналмалы қозғалысына қолдану. Теорема: Қандай да бір қозғалмайтын центрге қатысты алынған механикалық жүйенің кинетикалық моментінің уақыт бойынша алынған туындысы сол центрге қатысты алынған жүйедегі сыртқы күштердің бас моментіне тең.
 (1)
(1)
Мұндай теңдеулерді әрбір нүкте үшін құруға болатындықтан олардың жалпы саны n жүйедегі нүктелер санына тең болады. Осы теңдеудегі n теңдеудің әрқайсысына сәйкес нүктелердің радиус векторы  -ге векторлық түрде көюейтіп, оларды бір- біріне қосамыз:
-ге векторлық түрде көюейтіп, оларды бір- біріне қосамыз:
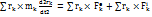 (2)
(2)
Осы теңдеуді ң сол жағын түрлендіреміз:
 =
= 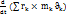 (3)
(3)
Жүйенің ішкі күштерінің қасиеті бойынша ішкі күштердің бас моменті әр уақытта нолге тең болады. Сондықтан да теңдіктің оң жағындағы екінші қосындысы нолге тең:
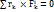 (4)
(4)
(3) ті(4) ке пайдаланып (2) келтіреміз:
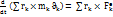
16. Қатты дене-ң жылжымайтын ості айналып қозғалу диф-қ теңдеуі. Декненің қозғалмайтын өс төңірегіндегі айналмалы қозғалысының дифференциалдық теңдеуін алу үшін кинетикалық моменттің өзгеруі туралы теореманы 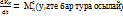
Теңдеулерінің үшінші түріне сәйкес қолдануымыз керек:
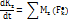
Дененің Z айналу осіне қатысты алынған кинетикалық моменті формулаларының 3-сі бойынша анықталады.

Дене абсолют қатты дене болған жағдайда  инерция мометі тұрақты шама болады. Олай болса алдыңғы теңдеуді былайша өзгерте аламыз.
инерция мометі тұрақты шама болады. Олай болса алдыңғы теңдеуді былайша өзгерте аламыз.
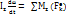 немесе
немесе 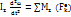
17Мех. жүйе-ң кинет. Эн-ы Ан-ма. Механикалық жүйенің кинетикалық эн-сы деп ондағы барлық материялық нүктелердің кинетикалық эн- ың қосындысына тең скаляр шаманы айтамыз. Массасы m әрбір материялық нүктенің кинетикалық эн-сы:
 (k= 1,2,n)
(k= 1,2,n)
Онда, анықтама бойынша, n материялық нүктеден тұратын механикалық жүйенің кинетикалық эн-сы осылардын арифметикалық қосындысына тең.
T= 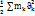 н/е T=
н/е T= 
Кинетикалық энергия қозғалыс мөлшерімен қатарлас келетін жүйе қозғалысының негізгі екі өлшемінің бірі болып табылады. Жоғарыда айтқанымыздай, жүйенің қозғалыс мөлшері оның ілгермелі қозғалысын сипаттайды. Ал кинетикалық энергия механикалық қозғалысыты толық көлемінде тереңірек сипаттайды.
Кинет. эн-я ан-ма: нүктенің кинет-қ эн-сы деп- оның массасы мен жылд-ң квад-ң көбейтіндісі-ң жартысыа тең шаманы айтамыз.
Т= m 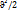
m  m
m 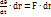
md 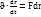 md
md  (m
(m 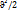 )=Fdr
)=Fdr
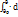 (m
(m 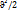 )=
)= 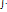 Fdr m
Fdr m 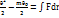
A=  толық жұмыс
толық жұмыс
d’A=Fdr элементар жұмыс
Теорема: матер-қ нүкте-ң кинет-қ эн-ң диффер-ы оған әсер ететін күш-ң элементар жұмысына тең.
dT=d’A
Теорема: Нүктенің қандай да бір орын ауыстыру-ғы кинет-қ эн-ң өзгеруі сол орын ауыс-ғы оған әсер етуші күш-ң жұмысына тең.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3930; Нарушение авторских прав?; Мы поможем в написании вашей работы!