Краткая теоретическая часть

ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА

ЛАБОРАТОРНАЯ РАБОТА №1-0

ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА.

Методическое указание к лабораторной работе № 1 – О.

Составители:	А.И.Горковенко
	И.Г. Фатеев

Т Ю М Е Н Ь 2002 г.

Цель работы: Изучение интерференционной картины на примере опыта Юнга.

Принадлежности: Гелий-неоновый лазер, оптическая скамья с линейкой, оправка с отверстиями, экран.

Пусть в некоторой точке пространства накладываются друг на друга две световые волны одинакового направления и одинаковой частоты, напряженности электрического поля которых равны 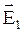и :

,

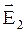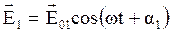. (1)

По принципу суперпозиции, напряженность результирующего поля равна их векторной сумме:

.

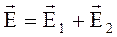В результате сложения двух гармонических колебаний одинаковой частоты получается колебание той же частоты, неизменная во времени амплитуда которого зависит от соотношения фаз складываемых колебаний, т.е.

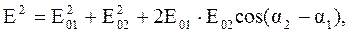(2)

которую проще всего найти с помощью векторной диаграммы, изображенной на рис.1.

Рис.1

Вводя интенсивности колебаний (J~ 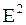), результат (2) можно записать в виде:

J=J₁+J₂+2 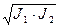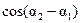. (3)

Если разность фаз Da = a₂ - a₁, возбуждаемых волнами колебаний остается постоянной во времени, то волны называются когерентными. Источники таких волн называются когерентными.

Для когерентных волн 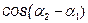имеет постоянное во времени (но свое для каждой точки пространства) значение.

В точках пространства, где 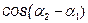>0, J > J₁+ J₂, где 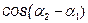<0, J < J₁+J₂. Таким образом, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией света.

Для некогерентных волн разность фаз Da=a₂-a₁ непрерывно изменяется, поэтому среднее во времени значение 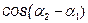равно нулю и интенсивность результирующей волны одинакова и равна J=J₁+J₂. Особенно отчетливо проявляется интерференция в том случае, когда интенсивности интерферирующих волн одинаковы: J₁=J₂. Тогда согласно (3) в минимумах J=0; в максимумах J=4J₁. Для некогерентных волн при том же условии получается всюду одинаковая освещенность J=2J₁.

Свет, испускаемый обычными (нелазерными) источниками, не бывает строго монохроматическим, т.е. имеющим неизменную частоту и амплитуду. Поэтому для наблюдения интерференции свет от одного источника нужно разделить на два пучка и затем их наложить друг на друга. Существующие экспериментальные методы получения когерентных пучков можно разделить на два класса. В методе деления волнового фронта пучок пропускается, например, через два близко расположенных отверстия в непрозрачном экране. Такой метод пригоден лишь при достаточно малых размерах источника. В методе деления амплитуды волнового фронта пучок делится на одной или нескольких частично отражающих, частично пропускающих поверхностях. Этот метод деления амплитуды может применяться и при протяженных источниках.

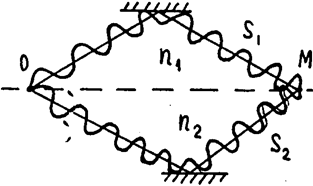Рис.2

Пусть разделение на две когерентные волны происходит в точке 0 (рис.2), До точки М первая волна проходит в среде с показателем преломления n₁ путь S₁, вторая волна проходит в среде с показателем преломления n₂ путь S₂. Если в точке 0 фаза колебания равна wt, то первая волна возбудит в точке М колебание 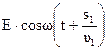, а вторая волна – колебание 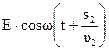, где u₁=с/n₁, u₂=с/n₂– соответственно фазовая скорость первой и второй волны.

Разность фаз d=Da двух когерентных волн от одного источника:

(4)

(учли, что 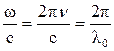, где l₀ – длина волны в вакууме). Произведение геометрической длины S пути световой волны в данной среде на показатель преломления n этой среды называется оптической длиной пути L, а D=L₂-L₁ – разность оптических длин проходимых волнами путей называется оптической разностью хода.

Если оптическая разность хода равна целому числу волн в вакууме:

D=±ml₀, (m=0, 1, 2, ……), (5)

то d=±2mp и колебания, возбуждаемые в точке М обеими волнами, находятся в одинаковой фазе. Таким образом, (5) есть условие интерференционного максимума.

Если оптическая разность хода:

D=±(2m+1)l₀/2, (m=0, 1, 2, ……), (6)

то d=±(2m+1)p и колебания, возбуждаемые в точке М обеими волнами, находятся в противофазе. Следовательно, (6) есть условие интерференционного минимума.

Впервые экспериментальная установка для демонстрации интерференции света осуществлена Томасом Юнгом в начале XIXв., схема опыта показана на рис.3. Яркий пучок солнечных лучей освещал экран А с малым отверстием S. Прошедший через отверстие свет вследствие дифракции образует расходящийся пучок, который падает на второй экран В с двумя малыми отверстиями S₁ и S₂, расположенными близко друг к другу на равных расстояниях от S.

Рис. 3

Интерференционная картина от двух когерентных источников света S₁ и S₂ регистрируется на экране Э. Интенсивность в любой точке М экрана, лежащей на расстоянии х от 0, определяется оптической разностью хода при n=1,

D=(S₂-S₁)×n=S₂-S₁. Из рис.3 видно, что

,

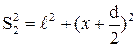откуда

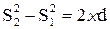(7)

Но 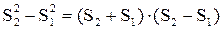, и т.к. из условия 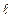>>d следует, что S₁+S₂ 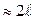, оптическая разность хода

. (8)

Подставив это значение D в (5) и (6), получим, что максимумы интенсивности будут наблюдаться при

(m= 0, 1, 2, ….), (9)

а минимумы – при

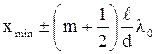, (m= 0, 1, 2, ….). (10)

Расстояние между соседними максимумами (или минимумами), называемое шириной интерференционной полосы D х, равно

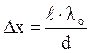(11)

(примерный вид показан на рис.4). Как видно из (11), D х не зависит от порядка интерференции (величины m)и является постоянной для данных 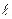, d и l₀.

В настоящее время для реализации опыта Юнга в качестве источника используют лазер. При этом для когерентного возбуждения вторичных источников S₁ и S₂ необходимость во вспомогательном отверстии S отпадает, так как в лазерном излучении световые волны когерентны по всему поперечному сечению пучка и щели вводят непосредственно в пучок лазерного излучения.

Дата добавления: 2015-06-04