Вопросы для допуска к работе

Э

Э

красный оранжевый желтый зеленый голубой синий фиолетовый

Рис.1

При прохождении через вещество электромагнитной волны, электрон в атоме вещества оказывается под воздействием силы Лоренца со стороны электромагнитного поля. Эта сила равна:

, (1)

где е - заряд электрона, 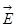- напряженность электрического поля, 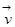- скорость электрона в веществе, - индукция магнитного поля, 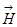- напряженность магнитного поля, связанная с индукцией соотношением (если m = 1).

Расчет показывает, что сила воздействия на электрон со стороны магнитного поля оказывается ~ в 10⁴ раз меньше силы воздействия электрического поля, поэтому вторым слагаемым в силе Лоренца можно пренебречь и считать, что на электрон действует только сила со стороны электрического поля. Так как эта сила изменяется по гармоническому закону, то она является вынуждающей силой, а колебания электрона - ВЫНУЖДЕННЫМИ КОЛЕБАНИЯМИ.

F=eE=eE₀sin (wt+a₀), (2)

где a₀ - начальная фаза колебания электрона, определяемая его координатами. Е₀ - амплитуда напряженности электрического поля, w - циклическая частота колебаний вектора в световой волне.

Кроме вынуждающей силы на электрон в атоме, исходя из наших упрощенных предположений, будет действовать возвращающая КВАЗИУПРУГАЯ СИЛА:

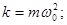F_упр= , (3)

где х - смещение электрона от положения равновесия, к - коэффициент жесткости, w₀ - СОБСТВЕННАЯ циклическая частота колебаний электрона в атоме.

Чтобы упростить вычисления, пренебрегаем затуханием за счет излучения. Тогда под действием этих сил электрон в атоме будет совершать колебательное движение, дифференциальное уравнение которое будет иметь вид:

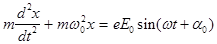. (4)

Из теории дифференциальных уравнений известно, что решение (4) имеет вид: x = x_maxsin(wt+a₀), где амплитуда

. (5)

Рассмотрим теперь электронную теорию дисперсии. Для упрощения будем считать молекулы вещества неполярными, т.е. молекулы превращаются в диполи только под действием внешнего электрического поля. Кроме того, поскольку массы ядер велики по сравнению с массой электронов, пренебрежем смещением ядер из положения равновесия под действием световой волны. В этом приближении дипольный электрический момент молекулы можно представить в виде: p_i = ex_{i max}, где х_мах - максимальное смещение i - того электрона из положения равновесия под действием электромагнитной волны. Так как входящие в состав молекулы электроны имеют набор собственных частот колебания w_0i, то подставив формулу (5) в выражение для дипольного электрического момента молекулы, получим:

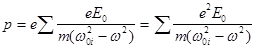. (6)

Обозначим число молекул в единице объема буквой N. Произведение Np дает вектор поляризации 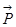, который, как следует из теории диэлектриков, равен P=Np=ce₀E, где e₀ - электрическая постоянная вакуума, c- диэлектрическая восприимчивость, связанная с диэлектрической проницаемостью вещества соотношением:

e =1+c, c= 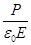. (7)

Так как показатель преломления для прозрачных диэлектриков , то 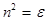откуда

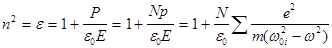. (8)

Как видно из (8) показатель преломления вещества является функцией частоты w падающего света (см. рис.2) и эта зависимость носит резонансный характер. Другими словами, при частотах, заметно отличающихся от всех собственных частот w_0i электронов, сумма в (8) будет мала по сравнению с единицей, так что n²» 1. Показатель преломления в этом случае растет с увеличением частоты падающего света ( > 0) и дисперсия носит название НОРМАЛЬНОЙ ДИСПЕРСИИ.

Вблизи каждой из собственных частот w_0i функция (8) терпит разрыв: при стремлении w к w_0i слева она обращается в + ¥, при стремлении справа - в - ¥ (пунктир на рис.2).

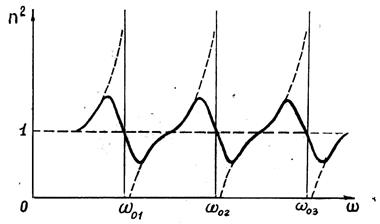
Рис.2

Такое поведение функции (8) обусловлено тем, что мы пренебрегли «трением излучения». Из теории колебаний следует, что при отсутствии трения амплитуда вынужденных колебаний при резонансе обращается в бесконечность. Учет трения излучения приводит к зависимости n² от w, показанной на рис.2 сплошной кривой. В области w» w_0i наблюдается падение показателя преломления с ростом частоты ( < 0). Эта область называется областью АНОМАЛЬНОЙ ДИСПЕРСИИ и соответствует резонансному поглощению света веществом.

Переходя от n² к n и от w к l , получим кривую n = f(l), изображенную на рис.3 (дан лишь участок кривой в области одной из резонансных длин волн l_0i). Участки кривой 1 -2 и 3 - 4 соответствуют области нормальной дисперсии ( < 0), а участок 2 - 3 - аномальной дисперсии ( >0).

Для всех прозрачных бесцветных веществ функция n = f(l) имеет в видимой части спектра характер, показанный на рис.3 участком кривой 3 - 4.

Как видно из рис.3, с ростом длины волны света, проходящего через вещество, показатель преломления падает. Отсюда следует, что наибольшее преломление в трехгранной призме испытывают фиолетовые лучи, в дисперсионном спектре фиолетовый цвет будет располагаться ближе к основанию призмы.

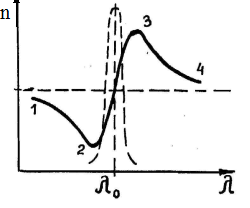
Рис.3.

2.Описание установки и метода измерений.

Используемый в работе метод основан на определении абсолютного показателя преломления (см. [1] раздел 2) вещества путем измерения угла d отклонения луча света от первоначального направления после преломления в призме (рис. 4)

А d_min

x y i_в

i_п

r₁ r₂

j C

D

B

Рис. 4

При выводе зависимости показателя преломления вещества n от угла отклонения d необходимо получить связь величины d с такими параметрами, как преломляющий угол призмы А (см. [1] раздел 2), угол падения луча на призму i_п, угол выхода луча из призмы i_в, углы r₁ и r₂.

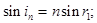
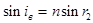, (9)

где n - абсолютный показатель преломления вещества призмы (n >1).

Сложив оба равенства (9) и сделав простые тригонометрические преобразования, получим:

;

;

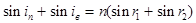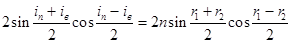(10)

Из рис. 4 видно, что угол d как внешний несмежный с углами внутренними x и y равен сумме этих углов, а углы x и y равны соответственно i_п - r₁ и i_в - r₂. Учитывая это, получим:

(11)

Так как j = А, как углы со взаимно перпендикулярными сторонами, а угол j = r₁ + r₂, как внешний несмежный с ними, то

А = r₁ + r₂. (12)

Подставляя (11) и (12) в (10) получаем:

. (13)

Эту формулу можно упростить. Зависимость угла отклонения луча d от угла падения i_п нелинейная и проходит через минимум. Если приравнять к нулю производную dd/di_п, можно найти условие, при котором наблюдается d_min. Расчеты показывают, что минимальный угол отклонения луча призмой будет в том случае, если угол падения луча i_п будет равен углу выхода i_в, при этом луч внутри призмы должен проходить перпендикулярно биссектрисе преломляющего угла А.

Из условия i_п = i_в следует, что r₁ = r₂. Подставляя оба равенства в (13), получаем формулу:

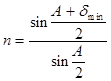(14)

Таким образом, измерив наименьший угол отклонения луча данной длины волны и зная преломляющий угол призмы, легко определить показатель преломления призмы для данной длины волны.

Для измерения угла наименьшего отклонения d_min между направлениями падающего и выходящего лучей служит гониометр Г-5, устройство которого показано на рис. 5.

Гониометр - прибор, дающий возможность измерять углы отклонения лучей, идущих от коллиматора (1). Коллиматор представляет собой оптическую систему, предназначенную для получения узкого параллельного пучка лучей, идущих от источника света, расположенного перед щелью (2). Регулировку ширины пучка производят с помощью винта (3), изменяющего ширину щели. На столике (4) может быть помещен любой исследуемый объект, а в данной работе здесь ставят стеклянную призму.

Рис. 5

Изображение дифракционной картины рассматривают в зрительную трубу (5), которая может поворачиваться вокруг вертикальной оси прибора вместе с алидадой (6), снабженной угломерным микроскопом (7), при ослабленном стопорном винте (9). Зрительная труба (5) снабжена фокусировочным винтом (8). Чтобы осуществить точную наводку зрительной трубы на исследуемый объект, винт (9) следует закрутить не применяя больших усилий и осуществить микроподачу винтом (10).

Отсчетное устройство состоит из алидады (6) и угломерного микроскопа (7), в поле зрения которого имеется шкала, показанная на рис. 3. Отсчетное устройство снабжено маховичком (11), дающим возможность привести шкалу в отсчетное положение.

Шкала микроскопа состоит из двух частей. В левом большом окошке изображены диаметрально противоположные участки лимба и вертикальный индекс для отсчета числа градусов и десятков минут. В правом маленьком окошек находится шкала с горизонтальным индексом, дающая возможность отсчитывать единицы минут и секунды.

Отсчетное устройство, смонтированное в алидаде (6), состоит из стеклянного лимба, на поверхность которого нанесена шкала с делениями. Лимб разделен на 1080 делений, цена деления 20”. Оцифровка делений произведена через 1^О. При помощи сложной оптической системы в отсчетный микроскоп передается изображение штрихов двух противоположных участков лимба и оптического микрометра, имеющего 600 делений.

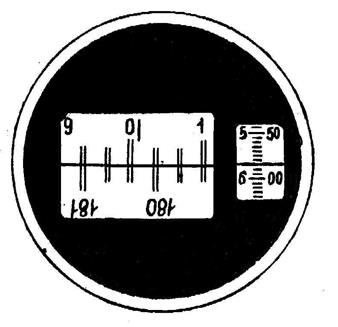
Рис. 6

Перемещая маховичок (11) (рис. 5) оптического микрометра можно совместить и развести изображения диаметрально противоположных участков лимба. При перемещении шкалы оптического микрометра на 600 делений верхнее изображение штрихов лимба смещается относительно нижнего на 10’. Следовательно, каждое деление шкалы оптического микрометра соответствует 1/600 от 10’, т.е. углу равному 1”.

Чтобы снять отсчет, прежде всего надо поставить шкалу гониометра в отсчетное положение, а для этого вращаем маховичок (11) до совмещения двойных штрихов на верхней и нижней половинах основной шкалы (рис.6).

Число градусов равно ближайшей слева к вертикальному индексу цифре. На рис. 6 отсчет соответствует 0^О. Число десятков минут равно числу интервалов двойных штрихов между штрихом, обозначающим целое число градусов и числом, отличающимся от него на 180^О и изображенным на нижней шкале в перевернутом виде. На рис. 6 имеем один интервал между штрихами 0 и 180, это соответствует 10’.

Число единиц минут и секунды определяем по правой шкале, которая имеет правую и левую стороны. На левой стороне шкалы горизонтальный индекс отмечает единицы минут, а на правой стороне - секунды. Отсчет, снятый по рис. 6 читается так: 0^О 15’ 57”.

2.Порядок выполнения работы.

1.Поместите перед щелью (2) коллиматора (1) (рис. 5) источник света - неоновую лампу.

2.Осторожно ослабив стопорный винт (9), установите зрительную трубу (5) так, чтобы в поле ее зрения была видна щель коллиматора. Закрепите стопорный винт (9), не прилагая больших усилий. Винтом точной наводки (10) совместите изображение щели с вертикальной нитью перекрестья окуляра зрительной трубы.

3.Винтом (3) отрегулируйте ширину щели коллиматора так, чтобы она была достаточно узкой и, вместе с тем, на ее фоне была четко видна нить перекрестья. Для фокусировки картины пользуйтесь винтом (8).

4.Снимите показания j₀ по шкале отсчетного микроскопа (7) (рис. 5). Отсчет j₀ будет соответствовать положению зрительной трубы Т₁ на рис. 7. Этот отсчет фиксирует положение неотклоненного луча. Отсчет величины j₀ повторите не менее трех раз. Результаты занесите в таблицу 1 и найдите среднее значение.

5.На столик (4) (рис. 5) поставьте призму так, чтобы биссектриса преломляющего угла А образовала с осью коллиматора угол a немного меньше прямого, как показано на рис. 7. Теперь луч света, идущий от коллиматора и отклоненный призмой не попадает в зрительную трубу, находящуюся в положении Т₁.

6.Ослабив стопорный винт (9), поверните зрительную трубу до положения Т₂, когда в поле зрения трубы появится ряд четких цветных изображений щели - линейчатый спектр неона, полученный при прохождении луча через призму.

7.Теперь следует найти такое положение призмы, при котором все линии спектра будут рассматриваться под углом наименьшего отклонения. Для этого поворачивайте столик с призмой в сторону неотклоненного луча, меняя тем самым, угол падения луча на призму. Сначала спектр будет двигаться вместе с призмой в сторону неотклоненного луча и угол отклонения d будет уменьшаться. Поворачивайте зрительную трубу за перемещающимся спектром так, чтобы он не уходил из поля зрения. При определенном положении призмы спектр останавливается и начинает движение в обратную сторону. Момент остановки спектра соответствует d_min. Зафиксируйте спектр в этом положении и больше не двигайте столик. Закрепите осторожно зрительную трубу стопорным винтом (9).

Т₁ a А K

j₀

B

d _min

j_i C

Т₂

Рис. 7

8.Перемещая с помощью микровинта (10) зрительную трубу, устанавливайте вертикальную нить перекрестья последовательно на красную, оранжевую, желтую и зеленую линии в спектре неона, каждый раз фиксируя по шкале отсчетного микроскопа углы, соответствующие положению зрительной трубы Т₂ (рис. 4). Отсчеты занесите в таблицу 1.

9.Рассчитайте углы d_min для четырех линий в спектре неона и найдите показатель преломления по формуле (6).

10.Постройте на миллиметровой бумаге график зависимости n = f(l).

Таблица 1

Цвет линии спектра	Длина волны	j0	j0ср	ji	dmin = ê ji - j0ср ê	n
красный
оранжевый
желтый
зеленый

1.В чем заключается явление дисперсии?

2.Как снять отсчет по шкале гониометра?

3.Как наблюдать дисперсию?

4.Как определить угол наименьшего отклонения луча d_min, прошедшего через призму?

5.Причина преломления света на границе раздела прозрачных сред.

Дата добавления: 2015-06-04