С использованием закона Брюстера

ПРЕЛОМЛЕНИЯ ВЕЩЕСТВА

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ

ПРОВЕРКА ЗАКОНА МАЛЮСА.

ЛАБОРАТОРНАЯ РАБОТА № 123

Вопросы к защите работы.

Вопросы для допуска к работе.

1.Какое явление используется в данной работе?

2.В каком случае можно наблюдать явление, используемое в данной работе?

3.Объясните смысл величин, входящих в рабочую формулу.

4. Какие величины необходимо измерить в данной работе?

5.Какие величины необходимо вычислить в этой работе?

1.Что представляет собой явление дифракции?

2.Вывести рабочую формулу.

3.Вывести условия max и min при дифракции света на одной щели.

4. Вывести условия max при дифракции света на дифракционной решетке

5. В чем особенности лазерного излучения?

6. Объяснить принцип работы лазера.

7.Какие причины могут вызвать полученную вами ошибку?

Литература

1.Методические указания к лабораторным работам по разделу “Оптика”. М.: МГАЛП, 1994

2.Методические указания к лабораторным работам по разделу “Оптика” “Лазерный оптический практикум”. М.: МГАЛП, 1993

3.И.В.Савельев. “Курс общей физики” т.2. “Наука” М. 1982 г.

4.Д.В.Сивухин. “Общий курс физики. Оптика”.1980г

Методические указания к лабораторной работе №122 по разделу физики “Оптика”. “Изучение явления дифракции лазерного излучения”.

Авторы: к.ф-м.н. Родэ Сергей Витальевич

Лицензия ЛР №021296 от 18.06.1998

Подписано к печати.................. № заказа............

Формат 60 х 88 1/16 МГУДТ, 113806

Бумага....................... ул. Садовническая, 33

Печать офсетная Типография МГУДТ, 113806

Объем в усл. печ. л................. ул. Садовническая, 33

Тираж..............экз.

Цель работы: изучение свойств поляризованного света, проверка законов Малюса и Брюстера.

Приборы и принадлежности: лазер типа ЛГ-52-3, анализатор, держатель образца с экраном, два образца исследования.

1. Теоретическое введение

Лазер, или оптический квантовый генератор (ОКГ),- источник оптического мощного, монохроматического, когерентного, остро направленного излучения.

Пионерские работы по созданию квантовых генераторов излучения радио и оптического диапазонов электромагнитных волн были в 1964г. удостоены Нобелевской премии (Н.Г.Басов и А.М.Прохоров от СССР и Ч.Таунс от США).

За прошедшее с тех пор время лазеры из лабораторных установок превратились в систему приборов, широко используемых в самых разнообразных технологических системах (от систем связи до систем обработки металлов).

ОКГ содержит два принципиально важных элемента: активную среду, являющуюся источником световой энергии, и оптический резонатор, внутри которого находится активная среда (рис.1).

Активная среда может быть твердой, жидкой или газообразной, но обязательно обладающей свойством усиливать свет на одной или нескольких частотах.

Все свойства лазерного излучения зависят исключительно от совокупности действия активной среды и резонатора. Выбор активной среды определяет длину волны генерации, предельную мощность и КПД. Выбор резонатора определяет пространственную и спектральную структуру излучения, реальную мощность и КПД.

В основе описания любой квантовой системы лежит идея Н.Бора о том, что электрон в атоме может обладать некоторым набором дискретных значений энергий - энергетических уровней.

В связи с этим атом может поглощать или излучать электромагнитные волны, которые обладают энергией, соответствующей разности энергий электрона на "разрешенных" для него уровнях.

Рис.1

1 - активная среда, 2 - оптический резонатор.

Представим себе, что электрон в атоме может переходить с уровня с энергией Е₁ на уровень Е₂ (пусть Е₂ > Е₁) и обратно.

Очевидно, что переходы с нижнего уровня на верхний не могут происходить самопроизвольно (спонтанно). Они могут быть осуществлены благодаря некоторому внешнему воздействию (например, внешнему излучению). Такой переход Е₁ ® Е₂ является индуцированным переходом. При этом происходит поглощение энергии внешнего излучения. Переход же с верхнего уровня на нижний может осуществляться как самопроизвольно (спонтанно), так и под действием внешнего излучения (индуцированный переход). При таком переходе происходит излучение энергии атомами активной среды. Поскольку механизм перехода с уровня Е₂ на уровень Е₁ может быть разным, то и излучение носит название, соответствующее механизму перехода, - СПОНТАННОЕ и ИНДУЦИРОВАННОЕ. Эти представления ввел в 1918 г. А.Эйнштейн.

Вероятность спонтанного перехода зависит только от свойств данного атома и не зависит от интенсивности падающего внешнего излучения. Индуцированные же переходы связаны как со свойствами атома, так и с интенсивностью внешнего вынуждающего излучения.

Исходя из термодинамических представлений, Эйнштейн доказал, что вероятность индуцированных переходов, сопровождающихся поглощением излучения, должна быть равна вероятности индуцированных переходов, сопровождающихся излучением. Другими словами, индуцированные переходы как в одном, так и в другом направлении осуществляются с равной вероятностью.

Индуцированное излучение обладает весьма важными свойствами. Направление его распространения в точности совпадает с направлением распространения вынуждающего излучения. Кроме того, в точности совпадают значения частот и фаз, а также плоскости поляризации индуцированного и вынуждающего излучения. Следовательно, вынуждающее и индуцированное излучения оказываются строго когерентными.

Эта особенность лежит в основе работы лазеров.

Таким образом, прохождение вынуждающего излучения через данную активную среду приводит к двум процессам: 1) ослаблению вынуждающего излучения за счет переходов Е₁ ® Е₂ и 2) усилению вынуждающего излучения за счет переходов Е₂ ® Е₁.

Для работы лазера необходимо преобладание второго процесса.

Чтобы выяснить, при каких условиях это осуществимо, рассмотрим механизм прохождения излучения через слой среды толщиной х.

Известно, что интенсивность света, проходящего через слой среды толщиной х, изменяется по закону

, (1)

где I - интенсивность излучения, падающего на среду, k – модуль коэффициента, который определяет характер взаимодействия излучения со средой. При k < 0 интенсивность уменьшается (происходит поглощение света веществом), при k > 0 - интенсивность увеличивается.

Из (1) следует, что

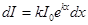; (2)

т.е. относительное изменение интенсивности излучения пропорционально толщине слоя dх.

С другой стороны, относительное изменение интенсивности излучения за счет переходов Е₂ ® Е₁ пропорционально энергии этого перехода Е₂ -E₁, числу атомов N₂, находящихся в состоянии Е₂ и времени dt прохождения вынуждающего излучения через слой dх.

Тогда

, (3)

где В₂₁ - коэффициент Эйнштейна (вероятность перехода Е₂ ® Е₁),

dt =(n/c) dx, (4)

где n - показатель преломления среды на участке dх, с - скорость света в вакууме.

Таким образом,

(5)

Сравнивая (5) и (3) получаем выражение для коэффициента k:

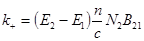(6)

По аналогии

(7)

Учитывая, что вероятности индуцированных переходов Е₂ ® Е₁ и

Е₁ ® Е₂ равны, т.е. В₂₁ = В₁₂ получаем:

. (8)

Из (8) совершенно очевидно, что условие усиления (k > 0) или ослабления (k < 0) интенсивности излучения зависит от знака разности N₂ –N₁.

В термодинамически равновесных системах распределение атомов по различным энергетическим состояниям определяется законом Больцмана:

, (9)

где Е_i - энергия данного состояния атома, Т - абсолютная температура, k - постоянная Больцмана, N_i - число атомов в данном энергетическом состоянии, N₀ - число атомов в основном состоянии.

Из этого уравнения следует, что заселенность уровней с меньшей энергией больше, чем уровней с большей энергией.

Значит в термодинамически равновесных системах N₂ < N₂ и k <0, т.е. интенсивность падающего излучения уменьшается.

Для осуществления усиления интенсивности (k >0) необходимо создать условия, при которых заселенность верхнего из пары уровней всегда превышала бы заселенность нижнего уровня (N₂ > N₁). Такая заселенность называется ИНВЕРСНОЙ ЗАСЕЛЕННОСТЬЮ. Системы, в которых осуществляется инверсная заселенность, являются термодинамически неравновесными.

Рассмотрим, каким образом создается инверсная заселенность на примере газового лазера, активной средой в котором служит смесь газов Не и Nе. В такой смеси газов зажигается электрический тлеющий разряд, в плазме которого и происходят основные процессы, обуславливающие работу лазера.

Напомним, что плазмой называют газ в сильно ионизированном состоянии при условии, что суммарный заряд электронов и ионов в каждом элементарном объеме равен (или почти равен) нулю. Плазма представляет собой особое (четвертое, наряду с твердым, жидким и газообразным) состояние вещества. Плазма, возникающая вследствие высокой температуры вещества, называется высокотемпературной или изотермической. Плазма, возникающая в тлеющем разряде, называется низкотемпературной или газоразрядной.

Электроны в газоразрядной плазме участвуют в двух движениях: 1) - хаотическом тепловом движении со средней скоростью и 2) - упорядоченном движении в направлении, противоположном направлению вектора напряженности электрического поля со средней скоростью < u >, гораздо меньшей, чем <v>. Под действием электрического поля кинетическая энергия электронов постепенно возрастает и достигает, в конце концов, значения, достаточного для того, чтобы возбудить или ионизировать молекулу. С этого момента часть столкновений электронов с молекулами перестает носить упругий характер и сопровождается большой потерей энергии электронами.

Обозначим е^* - те электроны, которые способны возбудить молекулы, а Nе^* и Не^* молекулы соответствующих газов в возбужденном состоянии. Кроме того, обозначим через е "медленные" электроны, т.е. такие электроны, которые отдали свою энергию молекулам газа, а Nе и Не - молекулы соответствующих газов, находящихся в основном (невозбужденном) состоянии.

Тогда процессы возбуждения, происходящие в плазме тлеющего разряда в смеси Не-Nе при неупругом столкновении электронов с молекулами газа, будут выглядеть следующим образом:

Ne + e^* = Ne ^*+ e; He + e^* = He^* + e (10)

Необходимо помнить, что рабочим газом в этой смеси является Nе.

Если бы все состояния возбужденного неона имели одинаковые характеристики, такие как время жизни, сечение (вероятность) возбуждения электронным ударом, они заселялись бы в соответствие с законом Больцмана (9).

Однако, эти характеристики различны для различных энергетических уровней. Поэтому заселенность уровней неона в тлеющем разряде может существенно отличаться от больцмановского.

Кроме того, переходы с испусканием кванта света (фотона) возможны лишь между теми уровнями, которые соответствуют определенным требованиям - правилам отбора. Эти правила можно строго обосновать с использованием законов квантовой механики.

С точки зрения создания инверсной заселенности целесообразно, чтобы верхний рабочий уровень имел большее сечение возбуждения и большее время жизни по сравнению с нижним.

Для дальнейшего понимания работы гелий-неонового лазера необходимо рассмотреть схему энергетических уровней Не и Nе, показанную на рис.2.

Из основного состояния 1s атом Не может перейти в состояния 2s (два уровня, отвечающие двум различным ориентациям спинов электронов возбужденного атома Не). Эти уровни не могут быть возбуждены оптически, т.к. переход 1s - 2s с поглощением фотона запрещен

правилами отбора. Возбуждение этих уровней возможно лишь за счет неупругих столкновений электронов с атомами (по схеме (10)).

Обратный переход 2s - 1s с излучением фотона также запрещен пра-

Рис.2.

вилами отбора. Возбуждение этих уровней возможно лишь за счет неупругих столкновений электронов с атомами (по схеме (10)).

Обратный переход 2s - 1s с излучением фотона также запрещен.

Уровни 5s и 4s атома неона близки по энергиям к уровням 2s гелия. При столкновении атомов гелия в состоянии 2s с атомами неона в основном состоянии происходит передача энергии от атомов гелия к атомам неона по схемам

; (11)

Процесс передачи энергии от атомов Не к атомам Nе показан на рис.2 жирной горизонтальной стрелкой.

Для неона разрешены оптические (с излучением фотона) переходы из состояний 4s и 5s в состояние 3p и дальше в состояние 3s. Поэтому убыль электронов на уровнях 4s и 5s неона осуществляется за счет излучения.

Как показали специальные исследования, время жизни состояний 4s и 5s атома неона составляет 10^-6с, а состояния 3p -10^-8с. В силу этого в газовом разряде при непрерывной подкачке энергии, т.е. пополнении уровней 4s и 5s, создается стационарная инверсная заселенность уровней неона 4s и 5s относительно уровней 3p.

Переходы 5s ® 3p (на рис.2 они показаны волнистой сплошной стрелкой) сопровождаются излучением в видимой области спектра. Переходы 4s ® 3p (на рис.2 они показаны волнистой пунктирной стрелкой) - сопровождаются излучением в инфракрасной области спектра. Переходы же 3p ® 3s (белая стрелка на рис.2) существенны только в том смысле, что с их помощью "очищаются" уровни 3p.

Усиление проходящего через газ потока излучения происходит только за счет индуцированных переходов 5s ® 3p и 4s ® 3p. Фотон, излучаемый при таком переходе, имеет направление, совпадающее с направлением фотона, вызывающего этот переход. Спонтанные же переходы приводят к появлению фотона, направление которого произвольно. Большое число спонтанных переходов нежелательно, т.к. не усиливая проходящего потока, спонтанное излучение нарушает инверсную заселенность верхних уровней атома.

Вероятность индуцированного перехода пропорциональна плотности вынуждающего излучения. Следовательно, для того, чтобы индуцированное излучение значительно превышало спонтанное, необходимо добиться высокой плотности усиливаемого излучения в веществе. Достигается это тем, что каждый фотон проходит активную среду несколько раз.

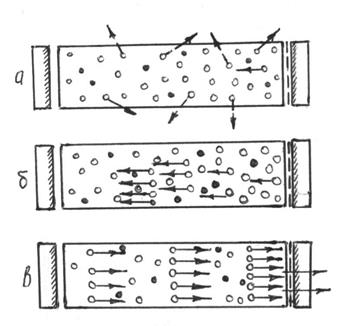Для осуществления такого многократного прохождения фотона через активную среду используют систему зеркал, расположенных у торцов трубки, содержащей активную среду (рис.1). Эта система зеркал носит название ЛАЗЕРНОГО РЕЗОНАТОРА.

Рис.3

- атомы Ne в основном состоянии

- атомы Ne в состояниях 5s и 4s

Одно зеркало резонатора имеет коэффициент отражения равный единице, а другое - "полупрозрачное". Оно имеет коэффициент пропускания от нескольких процентов до нескольких долей процента.

Процесс усиления излучения в резонаторе показан на рис.3 Отдельные фотоны, спонтанно излучаемые возбужденными атомами, имеют случайное направление. Эти фотоны и вызванные ими фотоны индуцированного излучения покидают активную среду, не вызывая усиления излучения вдоль оси лазера (рис.3а, пунктирные стрелки). Те же из фотонов, которые движутся вдоль оси активной среды (рис.3а, сплошная стрелка) вызывают индуцированное излучение фотона того же направления. Таким образом, число фотонов, летящих вдоль оси активной среды, растет, вовлекая в процесс индуцированного излучения все большее число возбужденных атомов. Процесс нарастает лавинообразно (рис.3б).

Те же из фотонов, которые движутся вдоль оси активной среды (рис.3а, сплошная стрелка) вызывают индуцированное излучение фотона того же направления. Таким образом, число фотонов, летящих вдоль оси активной среды, растет, вовлекая в процесс индуцированного излучения все большее число возбужденных атомов. Процесс нарастает лавинообразно (рис.3б).

Отражаясь от непрозрачного зеркала, это излучение вновь движется вдоль активной среды, вызывая все новые индуцированные переходы и, тем самым, увеличивая поток индуцированного излучения. При "взаимодействии" с полупрозрачным зеркалом малая часть этого излучения выходит из активной среды, а большая часть излучения вновь возвращается в активную среду и, таким образом, продолжается процесс усиления потока индуцированного излучения. При этом выход спонтанного излучения становится пренебрежимо малым. Однако, бурный лавинообразный рост интенсивности излучения возможен лишь в первые моменты времени, т.к. затем часть излучения уходит через полупрозрачное зеркало и, кроме того, уменьшается заселенность верхних уровней и увеличивается заселенность нижних уровней, что замедляет процесс.

При работе в непрерывном режиме устанавливается равновесие между всеми этими процессами (излучение и возбуждение) и достигается стационарная плотность излучения лазера (рис.3в).

Значительная мощность и высокая степень когерентности лазерного излучения дает возможность наглядно показать и изучить некоторые специфические свойства электромагнитных волн оптического диапазона. Поэтому лазеры нашли широкое применение в лекционных демонстрациях и лабораторных практикумах.

2.Описание установки и метода измерений.

Принципиальная схема установки для проверки закона Малюса представлена на рис. 4.

4 3 2

1

Рис. 4

В качестве источника плоскополяризованного света используют газовый гелий-неоновый лазер типа ЛГ-52-3.

На оптической скамье (1) располагают лазер (2), поляризатор (3), служащий анализатором, а также измеритель относительной интенсивности лазерного излучения (4).

Явление поляризации света, методы получения поляризованного света и свойства поляризованных лучей подробно изложены в [1]. Поэтому здесь мы ограничимся напоминанием основных законов поляризованного света.

Закон Малюса имеет вид:

I = I₀cos²a, (12)

где I - интенсивность света, прошедшего через анализатор, а I₀ - интенсивность света, прошедшего через поляризатор, a - угол между плоскостями пропускания поляризатора и анализатора.

Поскольку лазер дает плоскополяризованное излучение, поляризатор в данной работе не нужен. Поэтому в уравнении (1) I₀ - интенсивность лазерного излучения, падающего на анализатор. Поворачивая анализатор в оправке, можно изменять угол a между плоскостью поляризации лазерного луча и плоскостью пропускания анализатора. Фиксируя при этом с помощью измерителя относительной интенсивности величину I, легко установить линейную зависимость отношения I/I₀ от cos²a, что соответствует уравнению (1).

Для изучения и проверки закона Брюстера (см. [1] стр. 93,94) используется тот факт, что при падении поляризованного света на диэлектрическую пластинку под углом Брюстера (a_Б), луч, в котором составляющая электрического поля Е параллельна плоскости падения, не отражается (см. [1] рис.6.5 на стр. 94). Поэтому, если сориентировать вектор Е лазерного излучения параллельно плоскости падения луча на изучаемый образец, то при угле падения, равном

a_Б = arctg n, (13)

отраженного луча не должно быть. В (2) величина n - показатель преломления материала исследуемого образца.

В реальном случае интенсивность отраженного света не убывает до нуля, а проходит через минимум при плавном изменении угла падения. Этот момент легко обнаруживается визуально.

Установка для изучения и проверки закона Брюстера изображена на рис.5.

Луч от лазера (1) падает на образец (6), закрепленный в оправке (4) винтом (7).

Для того чтобы вектор Е лазерного излучения был сориентирован параллельно плоскости падения луча, нужно воспользоваться анализатором (2).

Поляризованный луч, падающий на диэлектрическую пластинку, отражается на экран (5). Изменяя угол падения луча на образец путем вращения оправки (4) и измеряя по лимбу (3) угол Брюстера, соответствующий минимуму интенсивности отраженного луча, определяют показатель преломления n исследуемого образца.

6 5 2 1

7 4 3

Рис.5

Поляризованный луч, падающий на диэлектрическую пластинку, отражается на экран (5). Изменяя угол падения луча на образец путем вращения оправки (4) и измеряя по лимбу (3) угол Брюстера, соответствующий минимуму интенсивности отраженного луча, определяют показатель преломления n исследуемого образца.

3.Порядок выполнения работы.

Задание1. Проверка закона Малюса.

1.После включения лаборантом лазера установите на противоположном от лазера конце оптической скамьи датчик (3) измерителя относительной интенсивности лазерного излучения и включите его в измеритель, а измеритель включите в сеть. Настройте лазер и датчик так, чтобы луч лазера попадал точно в окошко датчика. Контроль за точностью настройки осуществляют по цифровому табло измерителя. Измеритель показывает интенсивность лазерного пучка в относительных единицах.

2.Поставьте между лазером и измерителем поляризатор-анализатор (2). Добейтесь, чтобы плоскость поверхности анализатора была перпендикулярна лучу лазера.

3.Поворачивая с помощью нарезного кольца анализатор в оправке вокруг горизонтальной оси, установите его в такое положение, чтобы интенсивность света, фиксируемая измерителем, была максимальна. В этом случае плоскость пропускания (оптическая плоскость) анализатора параллельна плоскости колебаний вектора Е в поляризованном лазерном луче.

4.Заметьте по красному указателю на лимбе анализатора (по любой шкале лимба) угол, соответствующий максимуму интенсивности. Затем, поворачивая анализатор на углы от 20⁰ до 70⁰ от первоначального положения, каждый раз отмечайте относительную интенсивность луча I, прошедшего через анализатор. Значения углов и интенсивностей (в условных единицах) занесите в таблицу 1.

5.Поскольку интенсивность поляризованного лазерного излучения I₀ постоянна, то величина I должна быть пропорциональна cos²a. Для проверки этого утверждения необходимо построить график зависимости I/I₀ = f (cos²a).

Задание2. Определение показателя преломления вещества с использованием закона Брюстера.

1.Выключите измеритель интенсивности и вместо него поставьте на оптическую скамью держатель образца (4) (см.рис.5) с экраном (5). Прикрепите к экрану лист белой бумаги. Вставьте в держатель образец (6) и закрепите его винтом (7). Образец представляет собой металлическую полоску с наклеенной на нее прозрачной диэлектрической пластинкой.

2.Проверьте правильность установки анализатора, как это сказано в п.2 задания 1.

3. Поставьте с помощью нарезного кольца анализатор в такое положение, чтобы красный указатель на его лимбе был в горизонтальном положении. При этом плоскость пропускания анализатора, совпадающая с направлением указателя, параллельна плоскости падения луча на диэлектрическую пластинку. В этом случае анализатор пропускает лазерное излучение с составляющей вектора Е параллельной плоскости падения.

4.Поворачивая держатель с образцом вокруг вертикальной оси, убедитесь визуально, что при определенном угле падения луча на образец интенсивность светового пятна на экране проходит через минимум. Угол падения луча на образец, при котором наблюдается этот минимум, соответствует углу Брюстера (a_Б). Зафиксируйте угол Брюстера для данного образца по лимбу держателя образца и запишите его в таблицу 2.

5.Повторите проделанные действия для другого образца, и полученные результаты также занесите в таблицу 2.

6.Вычислите показатели преломления образцов по формуле n = tga_Б

и запишите полученные результаты в таблицу.

Таблица 1

N п/п	I0	I	a	cosa	cos^2a	I/I0

Таблица 2

N образца	aБ	tgaБ = n

Дата добавления: 2015-06-04