Постулаты квантовой теории. Уравнение Шредингера (стандартные условия)

Рассмотрим важный частный случай независящего от времени гамильтониана: .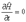

В этом случае существуют специальные решения уравнения Шрёдингера, которые легко получаются методом разделения переменных:

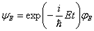, где не зависят от времени и являются (как и ) собственными векторами гамильтониана: .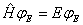

Собственные значения являются допустимыми значениями энергии системы, так как гамильтониан – оператор энергии, соответствующий классической функции Гамильтона.

Состояния называются стационарными состояниями. Их основные свойства таковы:

1) плотность вероятности и поток вероятности в этих состояниях не зависят от времени: .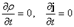

2) Средние значения наблюдаемых не зависят от времен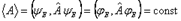и: при .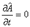

3) Вероятность обнаружить собственное значение 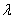наблюдаемой не зависит от времени:

.

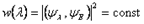Произвольное (нестационарное) состояние может быть разложено по стационарным состояниям – собственным векторам гамильтониана:

.

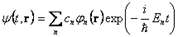В нестационарном состоянии энергия не имеет определенного значения, но среднее значение ее от времени не зависит:

, так как 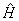- интеграл движения: .
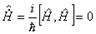Если наблюдаемая не коммутирует с гамильтонианом, то ее среднее, как и должно быть, зависит от времени (даже при ): .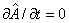

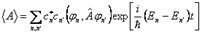Присутствие здесь недиагональных матричных элементов оператора наблюдаемой отражает характерный квантовомеханический эффект интер-

ференции различных стационарных состояний.

Легко проверить, что в нестационарном состоянии и также зависят от времени.

Дата добавления: 2015-06-04