Задачи к экзамену по квантовой механике

1. Вычислить оператор 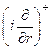, где r - радиальная координата сферической системы координат.

2. Показать, что когерентное состояни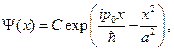е где 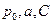- вещественные постоянные, минимизирует соотношение неопределенностей Гейзенберга.

3. Найти с.ф. и с.з. оператора .

4. Рассчитать коммутаторы .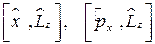

5. Найтисвязь между средними значениями координаты и импульса двух частиц, волновые функции которых 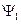и 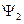связаны соотношением: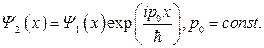

6. Система описывается волновой функцией

,

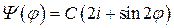где 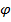– угол поворота вокруг оси z. Найти распределение вероятностей проекции момента импульса на ось z.

7. Состояние частицы массой 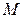задается волновой функцией

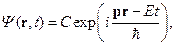
где 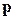– импульс частицы, 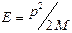- энергия частицы, 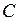- нормировочная константа. Найти плотность потока вероятности этой частицы.

8. Найти вероятность отражения частицы от потенциального барьера типа «ступенька».

9. Записать гамильтониан атома гелия.

10. В момент времени t = 0 волновая функция частицы в потенциальной яме с бесконечно высокими стенками (0 < x < a) имела вид 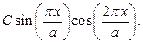Найти волновую функцию этой частицы для t> 0.

11. Волновая функция частицы в потенциальной яме с бесконечно высокими стенками

(0 < x < a) имеет вид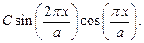

Найти распределение вероятностей энергии частицы.

12. Найти волновые функции и уровни энергии частицы в сферически симметричной потенциальной яме с бесконечно высокими стенками, если ее момент импульса равен нулю.

13. Найти дисперсию импульса гармонического осциллятора в первом возбужденном состоянии.

14. Волновая функция ротатора в сферических координатах имеет вид

.

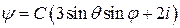Найти распределение вероятностей момента импульса ротатора.

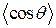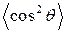15. Найти и в 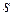-состоянии пространственного ротатора.

16. Найти среднее расстояние электрона до ядра в основном состоянии атома водорода.

17. Найти среднюю потенциальную энергию электрона в основном состоянии атома водорода.

18. Найти распределение вероятностей импульса электрона в основном состоянии атома водорода.

19. Рассматривая ядро атома урана как потенциальную яму шириной 10^-12 см, оценить частоту столкновений α-частицы с ее стенками с помощью соотношения неопределенностей Гейзенберга.

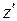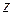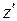20. Частица со спином ½ находится в состоянии с определенным значением проекции спина на ось z, равным +1/2. Определить вероятности возможных значений проекции спина на ось , если угол между осями и равен .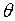
Найти дисперсию этой проекции.

21. Для заряженной частицы, находящейся в одномерной бесконечно глубокой потенциальной яме в основном состоянии найти сдвиги энергетических уровней в однородном электрическом поле (направленном вдоль оси x) в первом порядке теории возмущений.

22. Найти расщепление первого возбужденного уровня энергииплоского гармонического осциллятора с массой M и частотой ω под действием возмущения 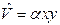((x, y) — плоскость колебаний).

23. Определить вероятность перехода заряженной частицы, находившейся в потенциальной яме (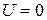 при 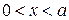) с бесконечно высокими стенками в основном состоянии, в первое возбужденное состояние под действием слабого переменного электрического поля .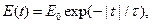

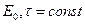24. Найти энергию и волновую функцию первого возбужденного состояния одномерного осциллятора. В качестве пробной функции взять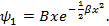

Дата добавления: 2015-06-04