
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическая основа карт 1 страница
|
|
|
|
Учебно-методическое пособие
Барнаул 2011
УДК 528. 9
Рецензенты:
Заведующий кафедрой «Физической географии и ГИС» АГУ, д.г.н., профессор А.Ш. Хабидов.
Доцент кафедры «Землеустройства, земельного и городского хозяйства» АГАУ, к.б.н В.А. Мерецкий.
Е.Г. Ещенко Математическая основа карт: учебно-методическое пособие.- Барнаул: Изд-во АГАУ, 2011.- 74 с.
Учебно-методическое пособие предназначено для изучения теоретических основ раздела «Математическая основа карт» и выполнения лабораторно–практических работ по дисциплине «Картография».
Пособие содержит теоретический материал по изучаемой теме, который поможет студенту научиться распознавать картографические проекции, вычислять и строить некоторые виды проекций.
Предназначено для подготовки бакалавров очного и заочного обучения по направлению 120700 «Землеустройство и кадастры».
Рекомендовано к изданию методической комиссией факультета природообустройства (протокол № 3 от 17 ноября 2011 г.).
© Ещенко Е.Г, 2011
© ФГБОУ ВПО АГАУ, 2011
© Издательство АГАУ, 2011
Содержание
| Теория математической основы карт | ||
| Задание 1. Определение картографических проекций | ||
| Задание 2. Вычисление нормальной равноугольной конической проекции (с двумя главными параллелями) | ||
| Задание 3. Вычисление нормальной равноугольной цилиндрической проекции | ||
| Приложения | ||
| Список используемой литературы | ||
Теория математической основы карт
Картографическая проекция – математически выраженные правила, по которым поверхность Земли проектируют на плоскость.
Проекция устанавливает однозначное соответствие между геодезическими координатами точек (широтой 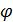 и долготой λ)и их прямоугольными координатами (
и долготой λ)и их прямоугольными координатами ( и
и  )на карте. Уравнения проекций в общей форме выглядят следующим образом:
)на карте. Уравнения проекций в общей форме выглядят следующим образом:
 );
); 
Конкретные реализации функций f1и f2часто выражены довольно сложными математическими зависимостями, их число бесконечно, а следовательно, разнообразие картографических проекций практически неограниченно. Проекция должна удовлетворять следующим условиям:
1. каждая точка эллипсоида ( и λ) изображается на плоскости соответствующей точкой
и λ) изображается на плоскости соответствующей точкой 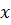 и
и  ;
;
2. изображение должно быть непрерывным.
Картографические проекции обычно различают по характеру искажений и по виду вспомогательной геометрической поверхности, с помощью которой сеть меридианов и параллелей с эллипсоида (шара) переносят на плоскость. Практически ценным является подразделение по территориальному охвату. По территориальному охвату выделяются картографические проекции для карт мира, полушарий, материков и океанов, карт отдельных государств и их частей. По этому принципу построены таблицы – определители картографических проекций.
По характеру искажений, возникающих при изображении поверхности Земли на плоскости картографические проекции делят на равноугольные (конформные), равновеликие (эквивалентные), равнопромежуточные (эквидистантные), произвольные.
Равновеликие (эквивалентные) проекции – сохраняют площади без искажений. Такие проекции удобны для измерения площадей объектов, однако, в них значительно нарушены углы и формы, что особенно заметно для больших территорий (рис. 1).
Равнопромежуточные (эквидистантные) проекции - произвольные проекции, вкоторых масштаб длин по одному из главных направлений постоянен и обычно равен главному масштабу карты. Соответственно различают проекции равнопромежуточные по меридианам -в нихбез искажений остается масштаб вдоль меридианов, и равнопромежуточные по параллелям -в них сохраняется постоянным масштаб вдоль параллелей. В таких проекциях присутствуют искажения площадей и углов, но они уравновешиваются (рис. 2).
Произвольные проекции - это все остальные виды проекций, в которых в тех или иных произвольных соотношениях искажаются и площади, и углы (формы). При их построении стремятся найти наиболее выгодное для каждого конкретного случая распределение искажений, достигая некоторого компромисса. Например, выбирают проекции с минимальными искажениями в центральной части карты, «сбрасывая» все сжатия и растяжения к краям. Частным случаем произвольных проекций являются равнопромежуточные проекции.
Равноугольные (конформные) проекции - оставляют без искажений углы иформы контуров, показанных на карте. Элементарная окружность в таких проекциях всегда остается окружностью, но размеры ее сильно меняются. Такие проекции особенно удобны для определения направлений и прокладки маршрутов по заданному азимуту, поэтому их всегда используют на навигационных картах. Однако карты, составленные в равноугольных проекциях, имеют значительные искажения площадей (рис. 3).

Рис. 1. Искажения в равновеликой цилиндрической проекции.

Рис. 2. Искажения в равнопромежуточной цилиндрической проекции.

Рис. 3. Искажения в равноугольной цилиндрической проекции.
Вспомогательными поверхностями при переходе от эллипсоида или шара к карте могут быть плоскость, цилиндр, конус, серия конусов и некоторые другие геометрические фигуры.
Картографические проекции делят на азимутальные, цилиндрические, конические, условные, многогранные.
Такая классификация является результатом развития теории картографических проекций.
Азимутальные проекции. Это проекции, в которых параллели - полные концентрические окружности, меридианы - их радиусы, углы между которыми равны соответствующим разностям долгот (рис. 5, в) Они выгодны для изображения материков, территорий с округлой конфигурацией. Изображения около точки касания плоскости земного эллипсоида почти не искажается. Точка касания является точкой нулевых искажений.
В зависимости от положения точки касания плоскости на поверхности земного эллипсоида проекции делятся (рис. 4):
- нормальные (полярные), когда плоскость касается Земли в одном из полюсов; вид сетки: меридианы – прямые линии, радиально расходящиеся из полюса, параллели – концентрические окружности с центрами в полюсе.
- поперечные (экваториальные), когда плоскость касания эллипсоида в одной точке экватора; вид сетки: средний меридиан и экватор – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии (могут быть и прямыми).
- косые (горизонтальные), когда плоскость, касается эллипсоида в какой – либо точке, лежащей между полюсом и экватором. В косых проекциях только средний меридиан, на котором расположена точка касания, представляет собой прямую, остальные меридианы м параллели – кривые линии.

Рис. 4. Шар и его ортографические проекции
Цилиндрические проекции. Это проекции, в которых меридианы изображаются равностоящими параллельными прямыми, а параллели - прямыми, перпендикулярными к меридианам (в общем случае не равноотстоящими) (рис. 5, а). Они выгодны для изображения территорий, вытянутых вдоль экватора. Искажения минимальны вблизи линии касания или двух линий сечения цилиндра земного эллипсоида, являющихся линиями нулевых работ.
В зависимости от ориентировки цилиндра относительно оси земного эллипсоида различают проекции:
- нормальные, когда ось цилиндра совпадает с малой осью земного эллипсоида; меридианы в этом случае представляют собой равноотстоящие параллельные прямые, а параллели – прямые, им перпендикулярные.
- поперечные, ось цилиндра лежит в плоскости экватора, вид сетки: средний меридиан и экватор – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии.
- косые, когда ось цилиндра составляет с осью эллипсоида острый угол; в косых цилиндрических проекциях меридианы и параллели – кривые линии.
Конические проекции. Это такие проекции, в которых параллели изображаются дугами концентрических окружностей (проведенных из одного центра), а меридианы - радиальные прямые, расходящиеся из общего центра проведения параллелей под углами, пропорциональными разности долгот (рис. 5, б). В этих проекциях искажения не зависят от долготы. Проекции применяют для территорий, вытянутых вдоль параллелей. Искажения мало ощутимы вдоль линии касания или двух линий сечения конуса земного эллипсоида, которые являются линией нулевых искажений.
Конические проекции делятся:
- нормальные, когда ось конуса совпадает с малой осью земного эллипсоида; меридианы этих проекций представлены прямыми линиями, расходящимися из вершины конуса, а параллель – дугами конических окружностей.
- поперечные, когда ось конуса лежит в плоскости экватора; вид сетки: средний меридиан и параллель касания – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии.
- косые, ось конуса составляет осью эллипсоида острый угол; в косых конических проекциях меридианы и параллели – кривые линии.
В нормальных цилиндрических, азимутальных и конических проекциях картографическая сетка ортогональна – меридианы и параллели пересекаются под прямыми углами, это главный признак этих проекций.
В проекциях существуют линии и точки, где искажения отсутствуют и сохраняется главный масштаб карты – это линии точки нулевых искажений.
Условные проекции - проекции, для которых нельзя подобрать простых геометрических аналогов. Их строят, исходя из каких-либо заданных условий. Например, желательного вида географической сетки, того или иного распределения искажений на карте, заданного вида сетки и др. К условным проекциям принадлежат псевдоцилиндрические, псевдоконические, псевдоазимутальные и другие проекции, полученные путем преобразования одной или нескольких исходных проекций.
Псевдоцилиндрические проекции - проекции, в которых параллели - прямые линии (как и в нормальных цилиндрических проекциях), средний меридиан - перпендикулярная им прямая, а остальные меридианы - кривые, увеличивающие свою кривизну по мере удаления от среднего меридиана (рис. 5, г). Чаще всего эти проекции применяют для карт мира и Тихого океана.
Псевдоконические проекции - такие, в которых все параллели изображаются дугами концентрических окружностей (как в нормальных конических), средний меридиан - прямая линия, а остальные меридианы -кривые, причем кривизна их возрастает с удалением от среднего меридиана (рис. 5, д). Применяются для карт России, Евразии, других материков.
Поликонические проекции - проекции, получаемые в результате проектирования шара (эллипсоида) на множество конусов (рис. 5, е). В нормальных поликонических проекциях параллели представлены дугами эксцентрических окружностей, а меридианы - кривые, симметричные относительно прямого среднего меридиана. Чаще всего эти проекции применяются для карт мира.
Псевдоазимутальныепроекции - видоизмененные азимутальные проекции. В полярных псевдоазимутальных проекциях параллели представляют собой концентрические окружности, а меридианы - кривые линии, симметричные относительно одного или двух прямых меридианов (рис. 5, ж). Поперечные и косые псевдоазимутальные проекции имеют общую овальную форму и обычно применяются для карт Атлантического океана или Атлантического океана вместе с Северным Ледовитым.
Многогранные проекции - проекции, получаемые путем проектирования шара (эллипсоида) на поверхность касательного или секущего многогранника. Чаще всего каждая грань представляет собой равнобочную трапецию, хотя возможны и иные варианты (например, шестиугольник, квадрат, ромб). Разновидностью многогранных являются многополосные проекции, причем полосы могут «нарезаться» и по меридианам, и по параллелям. Такие проекции характеризуются тем, что искажения в пределах каждой грани или полосы совсем невелики, поэтому их всегда используют для многолистных карт.
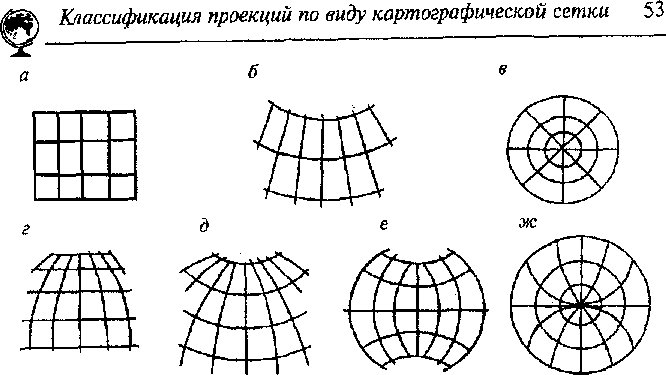
Рис. 5. Вид сетки меридианов и параллелей в разных картографических проекциях.
а – цилиндрическая; б – коническая; в – азимутальная; г – псевдоцилиндрическая;
д – псевдоконическая; е – поликоническая; ж - псевдоазимутальная
Задание 1. Определение картографических проекций
Цель задания. Изучить наиболее распространенные картографические проекции и уметь их распознавать по виду сетки меридианов и параллелей.
Задание. Определить картографические проекции географических карт в указанных ниже вариантах.
Указания к выполнению задания.
1. Ознакомиться с таблицами для определения проекций карт мира, полушарий, карт материков и их крупных частей, карт океанов, а также карт бывшего СССР и РФ (табл. 2, 3, 4, 5, 6). Таблицы-определители организованы по единому принципу: в заголовках столбцов формулируются вопроcы (условия); последовательно отвечая на них и переходя от левых столбцов к правым, область поиска в пределах строк сужается; в крайнем правом столбце приведено полное название иcкомой проекции, для которой выполняются свое условия внутри соответствующей строки.
2. Ознакомиться с картографическими проекциями предлагаемых географических карт (приложение 1). Для определения проекции выяснить:
- какая территория изображена на карте и по какой таблице следует проводить определение;
- какова форма рамки географической карты;
- какими линиями (прямыми, кривыми, дугами концентрических или эксцентрических окружностей) изображаются меридианы ипараллели, у концентрических окружностей промежутки между смежными окружностями, измеренные циркулем-измерителем, равны по величине, у эксцентрических вследствие разных радиусов кривизны – изменяются.
- как изменяются промежутки между параллелями по прямому (среднему) меридиану;
- каковы дополнительные сведения о проекции.
3. По таблице-определителю дать полное название картографической проекции, выяснить класс проекции по виду вспомогательной геометрической поверхности, использованной при ее построении, и по характеру искажений.
Результаты работы должны быть представлены в виде таблицы (табл. 1), как показано в приведенном ниже примере выполнения задания.
Пример выполнения задания.
Определить картографическую проекцию (Рис. 1).

|
Рис. 1. Карта СССР
На карте изображена территория бывшего СССР, поэтому определение следует проводить по таблице 7. Форма рамки - прямоугольная. Меридианы изображены прямыми, что легко проверить, приложив к линии меридиана линейку. Параллели изображены дугами концентрических окружностей: любые три точки этой линии, перенесенные на кальку, всегда можно совместить, поворачивая кальку, с разными частями этой линии; промежутки же между двумя соседними параллелями остаются постоянными. Таким образом, по виду картографической сетки проекция является нормальной конической.
Расстояния между параллелями по среднему меридиану остаются постоянными. Следовательно, проекция равнопромежуточная по меридианам. Используя дополнительные признаки проекции - уточняем по определителю (табл. 7) название нормальная коническая равнопромежуточная проекция Каврайского. Результаты определения проекции записываются в таблицу 2. Для некоторых картографических проекций (в частности для карт мира и карт океанов) дополнительные указания могут отсутствовать.
Таблица 1
Варианты заданий
| Номер варианта | Номер картогр.проекции (приложение 2) | Номер варианта | Номер картогр.проекции (приложение 1) |
| 2, 7, 26, 29 | 16, 20, 27, 36 | ||
| 5, 14, 21, 25 | 8, 15, 29, 39 | ||
| 3, 19, 24, 28 | 6, 19, 26, 28 | ||
| 4, 17, 20, 36, | 9, 22, 26, 39 | ||
| 3, 10, 23, 35 | 2, 12, 15, 27 | ||
| 16, 21, 26, 34 | 11, 17, 21, 30 | ||
| 9, 14, 23, 33 | 2, 5, 9, 13 | ||
| 18, 20, 28, 32 | 14, 16, 19, 38 | ||
| 7, 24, 31, 34 | 4, 19, 23, 37 | ||
| 11, 14, 23, 35 | 7,10, 18, 32 | ||
| 2, 12, 26, 38 | 15, 20, 22, 28 | ||
| 3, 13, 23, 33 | 5, 8, 25, 29 |

Таблица 3
Определитель проекций картографических сеток карт мира
| Какова форма рамки карты или вид всей сетки | Какими линиями изображаются меридианы и параллели | Как изменяются промежутки между параллелями по прямому меридиану с удалением от экватора | Название проекции |
| Сетка и рамка прямоугольник, полюс в рамке не изображается | прямыми | Сильно увеличиваются: между параллелями 70 и 800 приблизительно в четыре с половиной раза больше, чем между экватором и параллелью 100 | Нормальная цилиндрическая равноугольная проекция Меркатора |
| Увеличиваются: между параллелями 60 и 800 приблизительно 2,6 раза больше, чем между экватором и параллелью 200 | Нормальная цилиндрическая проекция Урмаева 1945 года | ||
| Увеличиваются: между параллелями 60 и 800 приблизительно 1,8 раза больше, чем экватором и параллелью 200 | Нормальная цилиндрическая проекция Урмаева 1948 года | ||
| Увеличиваются: между параллелями 70 и 800 приблизительно в 1,8 раза, чем между экватором и параллелью 100 | Нормальная перспективно – цилиндрическая проекция Голла (БСАМ) | ||
| Рамка прямоугольник, полюс в рамке карты не изображается | Параллели – прямыми, меридианы - кривыми | Увеличиваются: между параллелями 70 и 800 почти в 1,5 раза больше, чем между экватором и параллелью 100 | псевдоцилиндрическая проекция ЦНИИГАиК 1944года |
| Увеличиваются: между параллелями 60 и 800 почти 1,5 раза, чем между экватором и параллелью 200 | Псевдоцилиндрическая проекция Урмаева | ||
| Параллели - дугами эксцентрических окружностей, меридианы - кривыми | Сохраняются равными | Поликоническая проекция ЦНИИГАиК 1950 года | |
| Увеличиваются: между параллелями 70 и 800 приблизительно в 1,3 раза больше, чем между экватором и параллелью 100 | Поликоническая проекция ЦНИИГАиК (для БСЭ) | ||
| Дугами окружностей | Увеличиваются: между параллелями 70 и 800 приблизительно в 2,3 раза больше, чем между экватором и параллелью 100 | Круговая проекция Гринтена | |
| Рамка прямоугольник, полюс изображается рядом прямых | Параллели –прямыми, меридианы - кривыми | Сохраняются равными | Псевдоцилиндрическая эллиптическая проекция Каврайского |
| Сильно уменьшаются: между параллелями 80 и 900 более чем в пять раз меньше, чем между экватором и параллелью 100 | Псевдоцилиндрическая синусоидальная равновеликая проекция Каврайского | ||
| Сетка и рамка эллипс, полюс изображается точкой | Параллели – прямыми, меридианы - кривыми | Уменьшаются: между полюсом и параллелью 800 расстояние более чем в 2,5 раза меньше, чем между экватором и параллелью 100 | Равновеликая псевдоцилиндрическая проекция Мольвейде |
| кривыми | Уменьшаются: приполярный промежуток составляет приблизительно в 2,5 раза меньше приэкваториального | Производная равновеликая проекция Аитова - Гаммера | |
| Сетка с разрывами, полюс изображается несколькими точками | Параллели – прямыми, меридианы - кривыми | Уменьшаются: между полюсом и параллелью 800 расстояние примерно в 1,6 раза меньше, чем между экватором и параллелью 100 | Равновеликая псевдоцилиндрическая синусоидальная проекция Мольвейде – Гуда с разрывами |
| Сетка с разрывами, полюс изображается рядом прямых | Сильно уменьшаются: между полюсом и параллелью 800 расстояние примерно в 3,5 раза меньше, чем между экватором и параллелью 100 | Равновеликая псевдоцилиндрическая синусоидальная проекция БСАМ с разрывами |
Таблица 4
Определитель проекций картографических сеток карт полушарий
| Какими линиями изображаются параллели | Как изменяются промежутки по среднему (прямому) меридиану и экватору от центра полушария к его краям | Какой линией изображается экватор | Название проекции |
| окружностями или дугами окружностей | увеличиваются от 1 приблизительно до 2 | прямой | поперечная азимутальная равноугольная (стереографическая) проекция |
| равны | окружностью | нормальная азимутальная равноугольная (стереографическая) проекция | |
| окружностью | нормальная азимутальная равнопромежуточная проекция Посгеля | ||
| уменьшаются от 1 до 0,9 | окружностью | нормальная азимутальная равновеликая проекция Ламберта | |
| Прямыми | сильно уменьшаются | прямой | поперечная азимутальная ортографическая проекция |
| удалением от среднего меридиана к крайним | уменьшаются от 1 приблизительно до 0,7 | прямой | поперечная азимутальная равновеликая проекция Ламберта |
| уменьшаются от 1 приблизительно до 0,8 | поперечная азимутальная проекция Гинзбурга | ||
| равны | поперечная азимутальная равнопромежуточная проекция Посгеля | ||
| увеличиваются от 1 приблизительно до 2 | косая азимутальная равноугольная (cтepeoграфическая) проекция | ||
| уменьшаются от 1 приблизительно до 0.9 | косая азимутальная равновеликая проекция Ламберта |
Таблица 5
Определитель проекции картографических сеток карт и их материков
| Как изменяются промежутки между параллелями по среднему (прямому) меридиану от центра материка к северу и югу | Какими линиями изображаются параллели и меридианы | Как изменяются промежутки между соседними параллелями с удалением от среднего меридиана к западу и к востоку | Какой линией изображается экватор | Название проекции |
| Уменьшаются | Параллели и меридианы – кривыми, увеличивающими кривизну с удалением от среднего (прямого) меридиана к западу и востоку | увеличиваются | кривой | Косая азимутальная равновеликая проекция Ламберта |
| прямой | Поперечная азимутальная равновеликая проекция Ламберта | |||
| Параллели –концентрическими окружностей, меридианы - прямыми | уменьшаются | окружностью | Нормальная азимутальная проекция Ламберта | |
| Равны | Параллели –прямыми, меридианы - кривыми | Остаются постоянными | прямой | Равновеликая псевдоцилиндрическая синусоидальная проекция Сансона |
| Параллели – дугами концентрических окружностей, меридианы - кривыми | Дугой окружности | Равновеликая псевдоконическая проекция Бонна | ||
| Параллели – концентрическими окружностями, меридианы - прямыми | окружностью | Нормальная азимутальная равнопромежуточная проекция Постеля | ||
| Параллели- дугами концентрических окружностей, меридианы - прямыми | Дугой окружности | Нормальная коническая равноугольная проекция Каврайского 1934 года | ||
| Увеличиваются | Параллели- концентрическими окружностями, меридианы - прямыми | Остаются постоянными | окружностью | Нормальная азимутальная равноугольная (стереографическая) проекция |
| кривыми | увеличиваются | кривой | Косая азимутальная равноугольная (стереографическая) проекция |
Таблица 6
Определитель проекции картографических сеток карт океанов
| Какова форма рамки | Какими линиями изображаются параллели и меридианы | Как изменяются промежутки между параллелями по среднему (прямому) меридиану с удалением от экватора | Название проекции |
| Рамка - окружность | Параллели- концентрическими окружностями, меридианы - прямыми | увеличиваются | Нормальная азимутальная равноугольная (стереографическая) проекция |
| равны | Нормальная азимутальная равнопромежуточная проекция Постеля | ||
| Сетка и рамка – прямоугольник, полюс в рамке карты не изображается | прямыми | Сильно увеличиваются: между параллелями 70 и 800 приблизительно в четыре с половиной раза больше, чем между экватором и параллелью 100 | Нормальная цилиндрическая равноугольная проекция Меркатора |
| увеличиваются: между параллелями 60 и 800 приблизительно в 2,6 раза больше, чем между экватором и параллелью 200 | Нормальная цилиндрическая проекция Урмаева 1945 года | ||
| увеличиваются: между параллелями 60 и 800 приблизительно в 1,8 раза больше, чем между экватором и параллелью 200 | Нормальная цилиндрическая проекция Урмаева 1948 года | ||
| Рамка – прямоугольник, полюс в рамке карты не изображается | Параллели – прямыми, меридианы - кривыми | Незначительно уменьшаются | Псевдоцилиндрическая синусоидальная проекция Урмаева (с небольшими искажениями площадей) |
| Уменьшаются: между параллелями 70 и 800 в 2,1 раза меньше, чем между экватором и параллелью 100 | Псевдоцилиндрическая синусоидальная проекция Урмаева | ||
| кривыми | Незначительно уменьшаются: между параллелями 60 и 700 в 1,1 раза меньше, чем между экватором и параллелью 100 | Поперечная с овальными изоколами проекция ЦНИИГАиК | |
| Рамка – прямоугольник, полюс изображается рядом прямых | Параллели – прямыми, меридианы - кривыми | Сохраняются равными | Псевдоцилиндрическая эллиптическая проекция Каврайского |
| Сильно уменьшаются: между параллелями 80 и 900 более чем в пять разменьше, чем между экватором и параллелью 100 | Псевдоцилиндрическая синусоидальная равновеликая проекция Каврвйского |
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 206; Нарушение авторских прав?; Мы поможем в написании вашей работы!