Центр системы параллельных сил

Рассмотрим систему n сил P_i, приложенных в точках A_i (x_i, y_i, z_i) и параллельных оси Ov c ортом l (рис.2).

Если заранее исключить случай системы, эквивалентной паре сил, нетрудно на основании предыдущего параграфа доказать существование ее равнодействующей R.

Определим координаты центра C (x_c, y_c, z_c) параллельных сил, то есть координаты точки приложения равнодействующей этой системы.

Воспользуемся с этой целью теоремой Вариньона, на основании которой:

M₀ (R) = Σ M₀ (P_i).

Рис.2

Вектор-момент силы можно представить в виде векторного произведения, поэтому:

М₀ (R) = r_c × R = Σ М_0i (P_i)= Σ(r_i × P_i).

Учитывая, что R = R_v ∙ l, а P_i = P_vi ∙ l и воспользовавшись свойствами векторного произведения, получим:

r_c × R_v ∙ l = Σ(r_i × P_vi ∙ l),

r_c ∙ R _v× l = Σ(r_i ∙ P_vi × l) = Σ(r_i ∙ P_vi)× l,

или:

[ r_cR_v - Σ(r_i P_vi)]× l = 0.

Последнее выражение справедливо только в том случае, если выражение в квадратных скобках равно нулю. Поэтому, опуская индекс v и учитывая, что равнодействующая R = Σ P_i, отсюда получим:

r_c = (Σ P_i r_i)/(Σ P_i).

Проектируя последнее векторное равенство на оси координат, получим искомое выражение координат центра параллельных сил:

x_c = (Σ P_i x_i)/(Σ P_i);

y_c = (Σ P_i y_i)/(Σ P_i); (2)

z_c = (Σ P_i z_i)/(Σ P_i).

Центр тяжести тел.

Координаты центров тяжести однородного тела.

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz, где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

Если разбить тело на элементарные части объемом ∆ V_i, то на каждую его часть будет действовать сила притяжения ∆ P_i, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.3), и к ней применимы все выводы предыдущей главы.

Рис.3

Определение. Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

Напомним, что удельным весом элементарной части тела называется отношение ее веса ∆ P_i к объему ∆ V_i: γ _i = ∆ P_i /∆ V_i. Для однородного тела эта величина является постоянной: γ _i = γ = P / V.

Подставляя в (2) ∆ P_i = γ _i ∙∆ V_i вместо P_i, учитывая последнее замечание и сокращая числитель и знаменатель на g, получим выражения координат центра тяжести однородного тела:

x_c = (Σ∆ V_i ∙ x_i)/(Σ∆ V_i);

y_c = (Σ∆ V_i ∙ y_i)/(Σ∆ V_i); (3)

z_c = (Σ∆ V_i ∙ z_i)/(Σ∆ V_i).

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоско­сти.

Если оси х и у расположить в этой плоскости симметрии, то для каждой точки с координатами 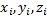можно отыскать точку с координатами . И координата по (3), бу­дет равна нулю, т.к. в сумме все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Действительно, в этом случае, если ось z провести по оси симмет­рии, для каждой точки с координатами 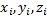можно отыскать точку с координатами 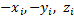и координаты и , вычисленные по фор­мулам (3), окажутся равными нулю.

Аналогично доказывается и третья теорема.

3) Если однородное тело имеет центр симметрии, то центр тя­жести тела находится в этой точке.

И ещё несколько замечаний.

Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (3) P_i – определять как вес соответствующей части и 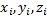– как координаты её центра тяжести.

Второе. Если тело однородное, то вес отдельной части его , где - удельный вес материала, из которого сделано тело, а V_i - объём этой части тела. И формулы (3) примут более удобный вид. Например,

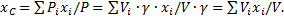
И аналогично, где - объём всего тела.

Третье замечание. Пусть тело имеет вид тонкой пластинки площадью F и толщиной t, лежащей в плоскости Oxy. Подставляя в (3) ∆ V_i = t∙ ∆F _i, получим координаты центра тяжести однородной пластинки:

x_c = (Σ∆ F_i ∙ x_i) / (Σ∆ F_i);

y_c = (Σ∆ F_i ∙ y_i) / (Σ∆ F_i).

z_c = (Σ∆ F_i ∙z _i) / (Σ∆ F_i).

где 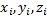– координаты центра тяжести отдельных пластин; 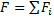– общая площадь тела.

Четвёртое замечание. Для тела в виде тонкого криволинейного стержня длиной L с площадью поперечного сечения a элементарный объем ∆ V_i = a ∙∆ L_i, поэтому координаты центра тяжести тонкого криволинейного стержня будут равны:

x_c = (Σ∆ L_i ∙ x_i)/(Σ∆ L_i);

y_c = (Σ∆ L_i ∙ y_i)/(Σ∆ L_i); (4)

z_c = (Σ∆ L_i ∙ z_i)/(Σ∆ L_i).

где 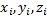– координаты центра тяжести i-го участка; .

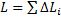Отметим, что согласно определению центр тя­жести - это точка геометрическая; она может лежать и вне преде­лов данного тела (например, для кольца).

Примечание.

В этом разделе курса мы не делаем разницы между силой притяжения, силой тяжести и весом тела. В действительности сила тяжести представляет собой разность между силой притяжения Земли и центробежной силой, вызванной ее вращением.

Координаты центров тяжести неоднородных тел.

Координаты центра тяжести неоднородного твердого тела (рис.4) в выбранной системе отсчета определяются следующим образом:

Рис.4

где - вес единицы объема тела (удельный вес)

- вес всего тела.

Если твердое тело представляет собой неоднородную поверхность (рис.5), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

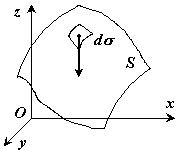
Рис.5

где 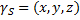- вес единицы площади тела,

- вес всего тела.

Если твердое тело представляет собой неоднородную линию (рис.6), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.6

где 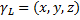- вес единицы длины тела,

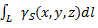- вес всего тела.

Дата добавления: 2015-06-04