Разрешающая способность дифракционной решетки

,

где Dl — наименьшая разность длин волн двух соседних спектральных линий (l и l+Dl,), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — полное число щелей решетки.

Угловая дисперсия дифракционной решетки

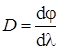
Линейная дисперсия дифракционной решетки

,

где F — фокусное расстояние линзы, проектирующей спектр на экран.

Формула Вульфа — Брэгга

,

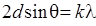где q — угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); d — расстояние между атомными плоскостями кристалла.

Разрешающая способность (разрешающая сила) объектива

,

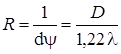где dy — наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются оптическим прибором, D - диаметр объектива, l - длина волны света.

Закон Брюстера

,

где e_B — угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n ₂₁ — относительный показатель преломления второй среды относительно первой.

Закон Малюса

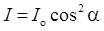
где I _о — интенсивность плоскополяризованного света, падающего на анализатор; I — интенсивность этого света после анализатора; a — угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления).

Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:

а) (в твердых телах),

где a — постоянная вращения; d — длина пути, пройденного светом в оптически активном веществе;

б) (в растворах),

где [a] — удельное вращение; r—массовая концентрация оптически активного вещества в растворе.

Релятивистская масса

,

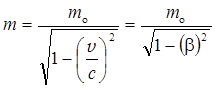где m _o — масса покоя частицы; v — ее скорость; с —-скорость света в вакууме; b— скорость частицы, выраженная в долях скорости света (b= v/с).

Взаимосвязь массы и энергии релятивистской частицы

,

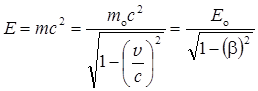где 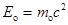— энергия покоя частицы.

Полная энергия свободной частицы

,

где Т — кинетическая энергия релятивистской частицы.

Кинетическая энергия релятивистской частицы

.

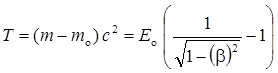Импульс релятивистской частицы

.

Связь между полной энергией и импульсом релятивистской частицы

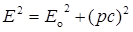
Закон Стефана—Больцмана

,

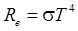где R_e — энергетическая светимость абсолютно черного тела, s — постоянная Стефана— Больцмана; Т — термодинамическая температура Кельвина.

Если тело не является абсолютно черным, то закон Стефана—Больцмана применяют в виде

,

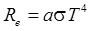где a— коэффициент (степень) черноты тела (a <1).

Закон смещения Вина

,

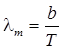где l _m — длина волны, на которую приходится максимум энергии излучения; b — постоянная Вина.

Максимальная спектральная плотность энергетической светимости абсолютно черного тела

,

где С ₁ = 1,29 10^-5 Вт/(м³ К⁵).

Энергия фотона

,

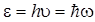где h — постоянная Планка; 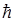— постоянная Планка, деленная на 2p; n — частота фотона; w — циклическая частота.

Масса фотона

.

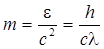где с — скорость света в вакууме; l — длина волны фотона.

Импульс фотона

.

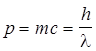Формула Эйнштейна для фотоэффекта

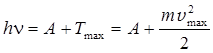
где h n — энергия фотона, падающего на поверхность металла; А — работа выхода электрона; T _max — максимальная кинетическая энергия фотоэлектрона.

Красная граница фотоэффекта

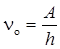, или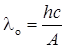

где n_o — минимальная частота света, при которой еще возможен фотоэффект; l_о — максимальная длина волны света, при которой еще возможен фотоэффект; h — постоянная Планка; с — скорость света в вакууме.

Формула Комптона

,

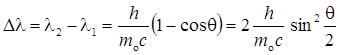где l₁ — длина волны фотона, встретившегося со свободным или слабосвязанным электроном; l₂ — длина волны фотона, рассеянного на угол q после столкновения с электроном; т _о — масса покоящегося электрона.

Комптоновская длина волны

.

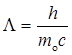Давление света при нормальном падении на поверхность

,

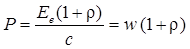где Е_е — энергетическая освещенность, w — объемная плотность энергии излучения; r — коэффициент отражения.

Момент импульса электрона согласно теории Бора для атома водорода

,

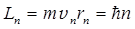где m — масса электрона; v_n — скорость электрона на n -й орбите; r_n — радиус n -й стационарной орбиты; ћ = h /2p — постоянная Планка; п — главное квантовое число (n = 1, 2,3,...).

Радиус n -й стационарной орбиты

,

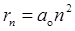где a _o — первый боровский радиус.

Энергия электрона в атоме водорода

,

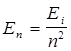где E_i — энергия ионизации атома водорода.

Энергия, излучаемая или поглощаемая атомом водорода,

,

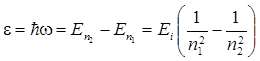где п ₁ и п ₂ — квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.

Спектроскопическое волновое число

,

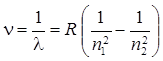где l — длина волны излучения или поглощения атомом; R — постоянная Ридберга.

Длина волны де Бройля

,

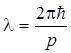где р — импульс частицы.

Импульс частицы и его связь с кинетической энергией Т:

a) 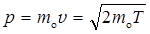при v << c (нерелятивистский случай),

б) 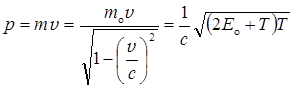при v £ c (релятивистский случай),

где т _о — масса покоя частицы; т — релятивистская масса; v — скорость частицы; с — скорость света в вакууме; Е _o — энергия покоя частицы (Е _o = т _о c ²)

Соотношение неопределенностей:

а) (для координаты и импульса),

где D р_x, — неопределенность проекции импульса на ось X,D х — неопределенность координаты;

б) 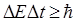(для энергии и времени),

где D E — неопределенность энергии; D t — время жизни квантовой системы в данном энергетическом состоянии.

Одномерное уравнение Шредингера для стационарных состояний

,

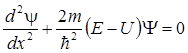где y= y(х) — волновая функция, описывающая состояние частицы; т — масса частицы; Е — полная энергия; U = U(x) — потенциальная энергия частицы.

Плотность вероятности

,

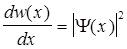где dw(x) — вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке dx.

Вероятность обнаружения частицы в интервале от х ₁ до х ₂

.

Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:

а) (собственная нормированнаяволновая функция);

б) 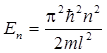(собственное значение энергии),

где п— квантовое число (п = 1, 2, 3,...); l— ширина ящика. В области 0 < x < l U =¥ и y(х)=0.

Массовое число ядра (число нуклонов в ядре)

,

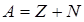где Z — зарядовое число (число протонов); N — число нейтронов.

Закон радиоактивного распада

, или ,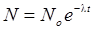

где dN — число ядер, распадающихся за интервал времени dt, N — число ядер, не распавшихся к моменту времени t; N _o — число ядер в начальный момент (t _o=0); l — постоянная радиоактивного распада.

Число ядер, распавшихся за время t,

.

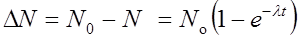В случае, если интервал времени D t, за который определяется число распавшихся ядер, много меньше периода полураспада T _1/2, то число распавшихся ядер можно определить по формуле

.

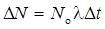Зависимость периода полураспада от постоянной радиоактивного распада

.

Среднее время t жизни радиоактивного ядра, т. е. интервал времени, за который число нераспавшихся ядер уменьшается в е раз,

.

Число атомов N, содержащихся радиоактивном изотопе,

,

где m— масса изотопа; m — молярная масса; N_a— постоянная Авогадро.

Активность А радиоактивного изотопа

,

где dN — число ядер, распадающихся за интервал времени dt; A _o — активность изотопа в начальный момент времени.

Удельная активность изотопа

.

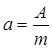Дефект массы ядра,

,

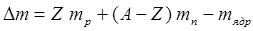где Z — зарядовое число (число протонов в ядре); А — массовое число (число нуклонов в ядре); (А—Z) — число нейтронов в ядре; m_p — масса протона; m_n — масса нейтрона; m_ядр — масса ядра.

Изменение энергии при ядерной реакции определяется соотношением

где å M ₁—сумма масс частиц до реакции и å M ₂—сумма масс частиц после реакции. Если å M ₁ > å M ₂, то реакция идет с выделением энергии, если же å M ₁ < å M ₂, то реакция идет с поглощением энергии. Отметим, что в последнюю формулу так же, как и при вычислении энергии связи ядра, мы можем подставлять массу изотопов, а не ядер, так как поправки на массу электронов оболочки входят с разными знаками и поэтому исключаются.

Энергия связи ядра

,

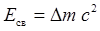где D m — дефект массы ядра; с — скорость света в вакууме. Во внесистемных единицах энергия связи ядра равна E _св= 931 D m, где дефект массы D m —в а.е.м.; 931— коэффициент пропорциональности (1 а.е.м.~931 МэВ).

Дата добавления: 2015-06-04