Изображение поверхности эллипсоида и шара на плоскости. Картограф проекции. Картограф сетки

З не обладает формой идеального шара. Фигура ее неправильна и немного сплюснута у полюсов. Земля также имеет общирные пологие выпуклости и вогнутости. Сложную фигуру нашей планеты, ограниченную уровенной поверхностью океана, называют геоидом. Наилучшее геометрическое приближение к реальной фигуре Земли дает эллипсоид вращения – геометрическое тело, образуется при вращении эллипса вокруг его малой оси. Для вычисления и уточнения размеров земного эллипсоида нужно рассчитать геометрически правильную фигуру – референц-эллипсоид, наилучшим образом приближенный к геоиду. Результаты во всех странах разные, поэтому в нашей стране принят референц-эллипсоид Красовского.

Картографическая проекция – это математически определенное отображение поверхности эллипсоида или шара на плоскости. Общие уравнения картограф проекции на плоскости: Х=f1 (φ,λ); Y= f2 (φ,λ) (система 1), где φ и λ – криволиненые географич координаты некоторой точки на картографируемой поверхности. X и Y – прямоугольные координаты изображения этой точки на плоскости в проекции, определяемой формулами f1 и f2. При условии, что эти функции однозначны и непрерывны (их число бесконечно, поэтому разнообразие картографических проекций неограниченно). Свойства проекции б. зависеть от свойств и характера этих функций.

Неизбежно возникают деформации – сжатия и растяжения, различные по величине и направлению. На карте возникает непостоянство длин и площадей. Виды искажений: длин – М карты непостоянен в различных точках и по разным направлениям, длины линий и рассеивания искажены; площадей – М площадей в различных точках карты различен, что является прямым следствием искажений длин и нарушает размеры объектов; углов – углы между направлениями на карте искажены относительно тех же углов на местности; форм – фигуры на карте дефор-ны, не подобны фигурам на местности, что связано с искажением углов. В ряде проекций существуют линии и точки нулевых искажений и изоколы – линии равных искажений длин, площадей, углов и форм.

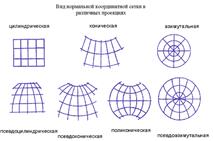
Каждой пропорции соответствует опрдел картографическая сетка меридианов и параллелей, которая составляет математ основу составляемых карт. Картографическая сетка – это изображение на карте линий меридианов и параллелей (географической сетки), отражающих значения долгот, счет которых ведется от начального Гринвич-го меридиана, и широт, которые отсчитываются от экваторара. Она показывает направление с-ю, з-в, позволяет судить о широтных поясах, о располажении объектов относительно стран света. Линии географической сетки наносят через равные интервалы: десятки градусов, градусы, минуты, секунды – все зависит от Масштаба и назначения карт.

Меридианы имеют математическое выражение: λ = const, параллели φ = const

Исключив из первой системы (1) широту φ, получим уравнения меридианов на плоскости: F1(x, y, λ) = 0. А исключив долготу λ, ур-я параллелей на плоскости: F2(x, y, φ) = 0. Картографическая сетка б. иметь наиболее простой вид, если х = f1(φ), y = f2(λ). В этом случае параллели и меридианы изображаются взаимно перпендикулярными прямыми. Если х – функция от (φ), y – функция от (φ,λ), то параллели – прямые, параллельные оси Y, а меридианы – криволинейные линии. Если х – функция от (φ,λ), y – функция от (λ), то меридианы – прямые, параллельные оси Х, параллели – кривые.

Система (1) позволяет получить проекции с разнообразными картографическими сетками, вид которых зависит от функций f1 и f2

8.Классификация картографический проекций. Все картограф проекции различают по четырем основн признакам: 1) по расположению полюса используемых сферических координат; 2) по характеру искажений; 3) по геометрии вспомогат поверхности; 4) по виду изображения меридианов и параллелей (по виду картографической сетки). по расположению полюса сферических координат. При картографировании территорий, содержащих географические полюсы, применяют сферические координаты, в которых полюсы оказываются обычными координатными точками. За координатные линии здесь принимают вертикалы и альмукантарата, аналогичные меридианам и параллелям, но их полюс Z не совпадает с географиче­ским полюсом Р (рис. 6.11).Переход от географических координат φ и λ любой точки сферы к ее сферическим координатам а и Z при заданном положении полюса Z (φ0,λ0) осуществляется по формулам сферической тригонометрии. по характеру искажений. Искажения присущи всем географ картам, построенным в разных картографич проекциях. Они различны по своему харак­теру и явл-ся одним из основных признаков классификации.Все картограф проекции по хар-ру искажений делятся на равноугольные, равновеликие и произвольные.Равноугольные сохраняют углы в любой точке карты. М в них зависит только от полож-я точки и не зависит от направления. Равновеликие проекции сохраняют пропорциональность площадей на карте к соответствующим площадям в натуре. Здесь эллипсы искажений всегда имеют одинаковую площадь, но сильно нарушают подобие фигур, отличаясь только формой и ориентировкой. Произвольные картографические проекции не относятся ни к равноугольным, ни к равновеликим. Из них выделяют равнопромежуточные, в которых один из главных М равен единице, и ортодромические, в которых большие круги шара (ортодромы) изобра­жаются прямыми. В проекциях, что чем больше искажения углов, тем меньше искажения площадей, и наоборот. Классификация по виду картографической сетки. В зависимости от видов меридианов и па­раллелей нормальной сетки картографические проекции делят на следующие классы.Цилиндрические проекции. Это проекции, в которых меридианы изображаются равностоящими параллельными прямыми, а параллели — прямыми, перпендикулярными к меридианам (в общем случае не равноотстоящими). Они выгодны для изображения территорий, вытя­нутых вдоль экватора. Примером является нормальная равноугольная цилиндрическая проекция Меркатора.Конические проекции. Это такие проекции, в которых параллели изображаются дугами концентрических окружностей (проведенных из одного центра), а меридианы — радиальные прямые, расходящиеся из общего центра проведения параллелей под углами, пропорциональны­ми разности долгот. В этих проекциях искажения не зависят от долготы. Проекции применяют для территорий, вытянутых вдоль параллелей. Все карты у нас составлены в конических проекциях.Азимутальные проекции. Это проекции, в которых параллели — полные концентрические окружности, меридианы — их радиусы, углы между которыми равны соответствующим разностям долгот. Они выгодны для изображения материков, территорий с округлой конфигурацией. Как пример — полярная равнопромежуточная азиму­тальная проекция Постеля.

Поликонические проекции. Это проекции, в которых параллели — части дуг эксцентрических окружностей малой кривизны, выпуклостью к экватору, центры проведения которых расположены на среднем меридиане. Меридианы — кривые малой кривизны, выпуклостью от среднего меридиана. Только экватор и средний меридиан — взаимо­перпендикулярные прямые.Псевдоцилиндрические проекции. Это проекции, в которых парал­лели — параллельные прямые (промежутки между которыми уменьша­ются от экватора к полюсам), меридианы — кривые линии, кроме среднего.Псевдоконические проекции. Это проекции, в которых параллели — окружности, средний меридиан — прямая, проходящая через их общий центр, остальные меридианы — кривые.Условные проекции. Это проекции, которые не входят ни в один из перечисленных классов. Параллели и меридианы — кривые самого различного вида.В зависимости от ориентировки вспомогательной поверхности (цилиндра, кону­са, плоскости, поликонусов) и картографической сетки в название проекции вносятся термины: нормальная, поперечная, косая.

9. Цилиндрические проекции. Виды проекции. Вспомогательными поверхностями при переходе от эллипсои­да или шара к карте могут быть плоскость, цилиндр, конус, серия конусов и некоторые другие геометрические фигуры.

Цилиндрические проекции — проектирование с шара (эллипсо­ида) ведется на поверхность касательного или секущего цилинд­ра, а затем его боковая поверхность разворачивается в плоскость. Если ось цилиндра совпадает с осью вращения Земли, а поверхность касается шара по экватору (или сечет его по паралле­лям), то проекция называется нормальной (прямой) цилиндричес­кой. Тогда меридианы нормальной сетки предстают в виде равно­отстоящих параллельных прямых, а параллели — тоже в виде пря­мых, перпендикулярных к ним. В таких проекциях меньше всего искажений в тропических и приэкваториальных областях.

Если ось цилиндра расположена в плоскости экватора, то это — поперечная цилиндрическая проекция. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют, и следовательно, в такой проекции наиболее выгодно изображать территории, вы­тянутые с севера на юг. В тех случаях, когда ось вспомогательного цилиндра расположена под углом к плоскости экватора, проекция называется косой цилиндрической. Она удобна для вытянутых тер­риторий, ориентированных на северо-запад или северо-восток.

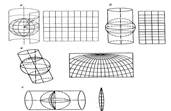
Рис.. Цилиндрические проекции:

а — развертка нормальной цилиндрической проекции (проектирова­ние на касательный цилиндр); б — нормальная цилиндрическая про­екция на секущий цилиндр; в — косая цилиндрическая проекция на секущем цилиндре; г— поперечная цилиндрическая проекция на ка­сательном цилиндре (особенно удобна для проектирования геодези­ческих зон).

Ортографическая проекция Ламберта. Центр проектирования находится в бесконечности, проектирование ведется пучком параллельных лучей. Свойства сетки:

- равновеликие свойства сетки вытекают из того, что площадь карты равна площади шара;

- сетка обладает равновеликими свойствами не только в целом, но и в частях. Поверхность сферического пояса равновелика соответствующей зоне ортографической проекции. Указанная проекция слабо искажает форму очертаний в экваториальных странах. С удалением от экватора искажение растет, следоват проекция пригодна для стран жаркого пояса;

Комфорная цилиндрическая проекция Меркатора. Построения сетки производятся на основании вычислений. Для обеспечения комформных свойств сетки необходимо кроме равенства углов обеспечить пропорциональное изменение сторон, т.к. параллели при переносе с глобуса на боковую поверхность цилиндра растягиваются пропорционально секансу широты. Меркатор увеличил дуги меридианов пропорционально секансу широты.

Свойства сетки:

- главный масштаб сохраняется по экватору карты;

- на параллелях частный масштаб увеличивается как у всех цилиндрических сеток, построенных на прямом цилиндре касательно глобусу на прямом экваторе;

- параллель с широтой 90 градусов уходит в бесконечность, поэтому сетка закончится на широте 75-80 градусов;

- масштаб площадей быстро увеличивается с удалением от экватора, на широте 60 градусов карты увеличены в 4 раза;

- искажение общих контуров стран, лежащих между экватором и широтой 60 градусов уже достигает заметной величины.

10.Конические проекции — поверхность шара (эллипсоида) проекти­руется на поверхность касательного или секущего конуса, после чего она как бы разрезается по образующей и разворачивается в плоскость. Различают нормальную (прямую) коническую проекцию, когда ось конуса совпадает с осью вращения З, поперечную коничес­кую — ось конуса лежит в плоскости экватора и косую коничес­кую — если ось конуса наклонена к плоскости экватора.

В нормальной конической проекции меридианы представляют собой прямые, расходящиеся из точки полюса, а параллели — дуги концентрических окружностей. По характеру искажений наибольшее распространение получили равноугольные и равнопромежуточные проекции.

В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий. В основе взглядов Птолемея на географическую науку лежит математический подход к составлению карт и определению положений городов и иных пунктов. Птолемей резко критикует подход, основанный лишь на использовании качественных описаний путешественников, без математической основы. Равнопромежуточные. Масштаб длин по одному из главных направлений (взаимно перпендикулярные направления, по одному из которых масштаб длин имеет наибольшее, а по другому — наименьшее значение) сохраняется постоянным. Искажения углов и площадей как бы уравновешиваются. Различают равнопромежуточные проекции по меридианам или параллелям. В них искажения длин отсутствуют по одному из направлений: либо вдоль меридиана, либо вдоль параллели

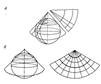Рис. Нормальная коническая проекция:

а - проекция на касательный конус и развертка; б - проекция на секущий конус и развертка.

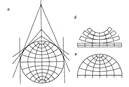Рис. Принцип построения поликонической проекции: а — положение конусов; б — полосы; в — развертка.

11.Азимутальные проекции — поверхность Земного шара (эллип­соида) переносится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная) азимутальная проекция. Парал­лели в ней являются концентрическими окружностями, а мериди­аны — радиусами этих окружностей. В этой проекции всегда кар­тогр-ют полярные области нашей и других планет.

Если плоскость проекции перпендикулярна к плоскости эквато­ра, то получается поперечная (экваториальная) азимутальная про­екция. Она всегда используется для карт полушарий. А если проектирование выполнено на касательную или секущую вспомога­тельную плоскость, находящуюся под любым углом к плоскости эк­ватора, то получается косая азимутальная проекция.

Можно показать, что азимутальные проекции являются пре­дельным случаем конических, когда угол при вершине конуса как бы становится равным 180°.

Среди азимутальных проекций выделяют несколько разновид­ностей, различающихся по положению точки, из которой ведется проектирование шара на плоскость.

Положение центра проектирования для азимутальных проекций

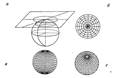
Азимутальные проекции:

а - нормальная (или полярная) проекция; б - сетка в полярной проекции-в - сетка в поперечной (экваториальной) проекции; г - сетка в косой ази­мутальной проекции.

Положение точки проектирования относительно шара (эллипсоида)	Название азимутальной проекции
В центре шара	Гномоническая
На противоположном конце диаметра	Стереографическая
За пределами шара на продол­жении диаметра	Внешняя
В бесконечности	Ортографическая

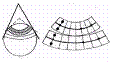
12. Псевдоцилиндричес. и псевдоконические проекции. Общие св-ва. Псевдоконические проекции – такие, в которых все параллели изображаются дугами концентрических окружностей (как в нормальных конических), средний меридиан – прямая линия, а остальные меридианы – кривые, причем кривизна их возрастает с удалением от среднего меридиана. Применяются для карт России, Евразии и др. материков. Нормальная сетка имеет вид: параллели – дуги концентрических окружностей, меридианы – кривые, симметричные относительно осевого меридиана. По характеру искажений они могут быть равновеликими и произвольными.

Псевдоцилиндрические проекции — проекции, в которых парал­лели — прямые (как и в нормальных цилиндрических проекциях), средний меридиан — перпендикулярная им прямая, а остальные меридианы — кривые, увеличивающие кривизну по мере удале­ния от среднего меридиана. Чаще всего эти проекции применяют для карт мира и Тихого океана.

13. Поликонические проекции Поликонические проекции – проекции, получаемые в результате проектирования шара (эллипсоида) на множество конусов. В поликонических проекциях земная поверхность переносится на боковые поверхности нескольких конусов, касательных к парал­лелям или секущих земной шар по заданным параллелям. На по­верхность каждого конуса переносится небольшой шаровой пояс земной поверхности. Затем каждый конус разрезается по образующей и разворачивается на плоскость. После склеивания полос получается поликоническая проекция. В простой поликонической проекции центральный (или средний) меридиан изображается прямой линией, остальные меридианы – кривыми, симметричными относительно центрального (среднего) меридиана, а параллели – разноцентренными окружностями, центры которых лежат на центральном (среднем) меридиане. Была принята видоизмененная поликоническая проекция, названная проекцией международной карты мира, масштаба 1:1 000 000 с поправками русского геодезиста Щеткина. Каждый лист этой карты ограничен по широте четырьмя, а по долготе шестью градусами. Меридианы изображены прямыми линиями. Масштаб по среднему меридиану несколько меньше единицы, а по крайним меридианам – несколько больше единицы. При склеивании 16 листов карты масштаба 1:1 000 000 возникают разрывы до 0,5 см. Поэтому склеивать более девяти листов нецелесообразно.

Общие свойства и искажения поликонических проекций

По принципу построения поликонические проекции незначи­тельно отличаются от конических.

Карты в поликонической проекции имеют следующие свойства:1)средний меридиан изображается прямой линией и не имеет искажения длин; поэтому поликонич проекция наиболее удоб­на д/изображений территорий, вытянутых вдоль меридиана. Остальные меридианы имеют вид кривых линий;2.параллели изображаются в виде дуг окружностей, проведен­ных из разных центров, лежащих на среднем меридиане3)нет нарастающего искажения масштабов к северу и югу, так как главный масштаб сохраняется по параллелям касания (се­чения) каждой полосы;4)проекция имеет искажения длин (масштаб карты не постоянен в разных точках и по разным направлениям, а длины линий и расстояния искажены) и углов (углы между направлениями на карте искажены относительно тех же углов на местности).

Эта проекция взята за основу для составления равноугольной международной проекции.

Многогранные проекции

В целях уменьшения искажения поверхность шара или эллипсоида делится меридианами и параллелями на трапеции. Каждая трапеция проектируется на плоскость. Если листы такой карты склеить так, чтобы между ними не было разрывов, то получится многогранник. Чем меньших размеров трапеция, тем больше граней у многогранника. Мир отображается на многолистной карте. Проекция каждого листа имеет свои параметры.

Многогранная картографическая проекция – проекция, параметры которой подобраны для отдельного листа или группы листов многолистной карты.

Примером является многолистная Международная карта мира масштаба 1:1000000. Каждый лист ограничен двумя меридианами и двумя параллелями. Протяженность листа по ширине составляет 4°, а по долготе - 6°; на широтах от 60 до 76° листы сдваивают, а выше 76° листы счетверяют.

Рисунок 6 – Схема многогранной проекции;

Многогранные проекции обладают одним недостатком, который обусловлен тем, что на плоскости листы не складываются по рамкам без разрывов. Если на плоскости стола разложить четыре или девять листов карты и попытаться их соединить по параллелям и меридианам, то обнаружится, что эти листы не стыкуются. Между ними обязательно обнаружится разрывы (рисунок 6). Для миллионной карты мира эти разрывы не очень большие, так что при склейки даже девяти листов они существенного влияния не оказывают.

Дата добавления: 2015-06-04