Квантовая гипотеза и формула Планка для описания излучения абсолютно черного тела

Пытаясь получить явное выражение для универсальной функции Кирхгофа, В. Вин предложил следующую формулу

, (5.4.1)

где а и b - некоторые параметры.

При определенном подборе параметров а и b выражение (5.4.1) дает достаточно хорошее совпадение с экспериментальными данными в области малых длин волн, но сильно расходится с экспериментальными значениями в области больших длин волн.

Дальнейшее исследование вида функции Кирхгофа методами классической физики предпринималось рядом ученых. Английские физики Джон Рэлей и Джеймс Джинс подошли к изучению спектральных закономерностей излучения абсолютно черного тела с позиций статистической физики, а с позиции не термодинамики, как это делали их предшественники. Они представили равновесное излучение в замкнутой полости с зеркальными стенками как систему пространственных стоячих электромагнитных волн. Частоты этих волн должны удовлетворять определенным условиям, подобным условиям для частот стоячих упругих волн в стержне, причем колебания с разными собственными частотами совершаются независимо друг от друга. Поэтому каждой собственной частоте соответствует своя колебательная степень свободы излучения абсолютно черного тела. С учетом возможных видов поляризации количество стоячих волн и связи испускательной способности абсолютно черного тела с равновесной плотностью энергии теплового излучения, У. Рэлей и Д. Джинс в 1900 г. получили выражение для универсальной функции Кирхгофа

, (5.4.2)

где - средняя энергия, которая приходится на одну колебательную степень свободы излучения равновесной системы.

Далее У. Рэлей и Д. Джинс используя закон классической статистической физики о равном распределении энергии по всем степеням свободы и предположив, что на каждое электромагнитное колебание приходится в среднем энергия, равная kT ( ‑ на электрическую и ‑ на магнитную энергию волны) определили среднюю энергию :

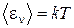. (5.4.3)

Подставив выражение (5.4.3) в (5.4.2) и получили соотношение:

, (5.4.4)

которое впоследствии назвали формулой Рэлея–Джинса.

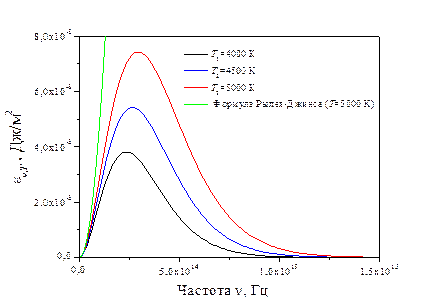
Формула Рэлея–Джинса хорошо согласуется с опытными данными только для малых частот (или больших длин волн) (рис. 5.4.1). Однако она не удовлетворяет закону смещения Вина, а также закону Стефана–Больцмана.

Например, для абсолютно черного тела энергетическая светимость , определяемая по формуле Рэлея–Джинса, оказывается равной бесконечности:

. (5.4.5)

А согласно закону Стефана–Больцмана (5.3.2) энергетическая светимость является конечной величиной. Формула (5.4.4) противоречит также закону сохранения энергии. Наиболее сильное расхождение между полученным по законам классической физики выражением (5.4.4) и экспериментальными данными наблюдается в области частот ультрафиолетового диапазона (рис. 5.4.3). Поскольку вывод формулы Рэлея–Джинса был безупречным в своей классической строгости и последовательности, решение проблемы описания теплового излучения в рамках классической физики оказалось невозможным в принципе. Это обстоятельство получило в физике образное название «ультрафиолетовая катастрофа». Выход из создавшейся ситуации нашел немецкий физик Макс Планк (1900 г.), который получил свою знаменитую формулу и тем самым заложил основы для построения квантовой оптики.

Для этого ему пришлось отказаться от положения классической физики, согласно которому энергия любой системы может изменяться только непрерывно, т.е. может принимать сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомы излучают энергию не непрерывно, а определёнными порциями – квантами, причём энергия кванта пропорциональна частоте колебания:

, (5.4.6)

где h = 6,626×10^-34 Дж×с – постоянная Планка.

Так как излучение испускается порциями, то его энергия e может принимать лишь определённые дискретные значения, кратные целому числу элементарных порций энергии e_ф:

e = nh n, (5.4.7)

где n = 0,1,2,3,….

Так как распределение энергии равновесного излучения по частотам зависит только от температуры и не зависит от свойства системы, с которой связано излучение, М. Планк выбрал наиболее простую модель излучающей системы в виде совокупности линейных гармонических осцилляторов (электрических диполей) со всевозможными собственными частотами n. Выполнив усреднение энергии излучения с частотой n с помощью функции распределения Больцмана, М. Планк получил выражение для среднего значения энергии, приходящейся на одну степень свободы излучения абсолютно черного тела:

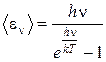. (5.4.8)

Подставив выражение (5.4.8) в (5.4.4) М. Планк получил формулу для универсальной функции Кирхгофа, которая блестяще согласуется с экспериментальными данными:

. (5.4.9)

Формула Планка описывает распределение энергии в спектре излучения абсолютно чёрного тела во всём интервале частот и температур. Чтобы решить эту задачу М. Планку пришлось сделать предположение совершенно чуждое классическим представлениям, а именно допустить, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов). Впервые Планк изложил теоретический вывод этой формулы в 1900 г. – этот день и стал днём рождения квантовой физики. Это событие ознаменовало новую эру в физике.

Из формулы Планка выводятся все законы теплового излучения.

1) Из формулы Планка можно получить формулой Рэлея-Джинса.

Рассмотрим области малых частот, т.е. h n<< kT (энергия кванта излучения мала по сравнению с энергией теплового движения). Разложим выражение в ряд, ограничившись двумя первыми членами разложения:

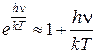. (5.4.10)

Тогда

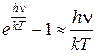. (5.4.11)

Подставляя (5.4.11) в формулу Планка (5.4.9), получим выражение:

, (5.4.12)

совпадающее с формулой Рэлея-Джинса (5.4.4).

2) Из формулы Планка можно вывести закон Стефана-Больцмана.

Найдем энергетическую светимость абсолютно черного тела:

. (5.4.13)

Введём безразмерную величину 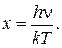Тогда:

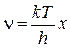, (5.4.14)

а

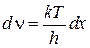. (5.4.15)

На основе формул (5.4.14-5.4.15), сделаем замену переменных в выражении (5.4.13):

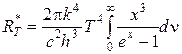. (5.4.16)

Учитывая, что 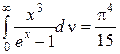, получим:

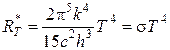, (5.4.17)

где – постоянная Стефана-Больцмана.

Из выражения (5.4.17) видно, что постоянная Стефана-Больцмана равна:

. (5.4.18)

Используя соотношение (5.4.18) М. Планк впервые определил значение постоянной Планка h = 6,626176×10^-34 Дж×с.

3) Закон смещения Вина также можно получить из формулы Планка.

Запишем формулу Планка (5.4.9) для переменных l и Т. Для этого воспользуемся выражение (5.1.6):

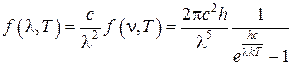. (5.4.19)

Введя , из (5.4.19) получим выражение:

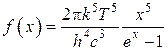. (5.4.20)

Найдем максимум функции (5.4.20):

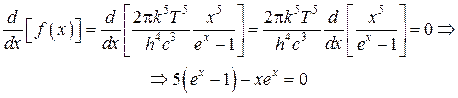. (5.4.21)

Решение этого трансцендентного уравнения методом последовательных приближений даёт x = 4,965. Учитывая это, получаем закон смещения Вина:

, (5.4.22)

где м×К – постоянная Вина.

4) Подставив x = 4,965 в выражения (5.4.20), найдем максимальное значение функции 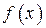и получим второй Вина:

, (5.4.23)

где С ₁ = 1,3×10^-5 Вт/(м³×К⁵) – вторая постоянная Вина.

Таким образом, формула Планка не только хорошо согласуется с экспериментом, но и содержит в себе частные законы теплового излучения. Формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Её решение стало возможно только благодаря революционной квантовой гипотезе Планка.

Дата добавления: 2015-06-04