Образец матрицы для анализа заданий

Обследуем	Задания	Сумма
a	b	c	d	е
1.
2.
3.
4.
5.
Сумма

Следующим шагом будет вычисление показателя, определяющего долю испытуемых, ответивших в соответствии с "ключом" опросника или индекса эффективности задания¹. Этот показатель подсчитывается делением количества обследуемых, давших правильный (так называемый "ключевой") ответ, на их общее количество. В идеале этот индекс для каждого задания должен располагаться в интервале от 0,25 до 0,75, приближаясь в среднем к 0,5 для всего опросника. Индекс, меньший чем 0,25, показывает, что задание неэффективно потому, что очень

немногие обследуемые отвечают на него правильно, а выше 0,75 указывает на то, что на данное задание получено слишком много правильных ответов. В табл. 3.3 анализа заданий индекс эффективности для каждого задания получается следующим образом: (a) 3/5 = 0,6; (b) 2/5 = 0,4; (с) 0/5 = 0; (d) 3/5 = 0,6 и (е) 5/5 = 1. Из этого следует, что нужно устранить задания (с) и (е) из окончательной версии опросника.

Также нужно удостовериться, просмотрев результаты в таблице анализа заданий, в том что хороший индекс эффективности, т. е. лежащий где-то посередине между крайними оценками, не просто означает выбор средних оценок в оценочном континууме каждым испытуемым, а представляет собой вариацию различных оценок.

Задания (вопросы, утверждения) только тогда следует включать в окончательную версию опросника, когда они измеряют те же самые личностные особенности, что и другие, предназначенные для этого задания. Для определения дискриминативности заданий используется коэффициент корреляции каждого задания с общим баллом всего теста. Чем выше коэффициент корреляции, тем выше дискриминантность задания, тем лучше задание. Это основной критерий. Как правило, требуется минимальная корреляция в 0,2. Задания с отрицательной или нулевой корреляцией почти всегда исключаются.

Для расчета этого показателя чаще всего применяется коэффициент произведения моментов Пирсона (заметим, что он наиболее приемлем для оценивания заданий, имеющих пять и более вариантов ответа, а в случае дихотомических заданий используется точечно-бисериальная корреляция). Вычисления обычно производятся с помощью специальных компьютерных программ, однако каждый разработчик тестов должен хотя бы один раз провести расчеты вручную. Это дает возможность проникновения в смысл того, что происходит с заданиями теста. Тем читателям, которые попытаются осуществить эту процедуру, напоминаем, что коэффициенты корреляции всегда меньше +1 и больше -1. Если получено значение коэффициента, выходящее за границы этого интервала, значит, допущена ошибка в расчетах. Формула коэффициента произведения моментов Пирсона имеет вид:

r =

n ∑ XY - ( ∑ X)( ∑ Y)

√[∑ X ² - (∑ X)²][ n ∑ Y ² - (∑ Y)²

,

где r - коэффициент корреляции; X - результат по каждому заданию; Y - балл (результат) по всему тесту; n - количество попарных произведений; ∑ - сумма. Для того чтобы подсчитать коэффициент корреляции произведения моментов Пирсона, нужны: сумма баллов испытуемых по каждому заданию (∑ Х), сумма баллов, испытуемых по всему тесту (∑ Y), сумма квадратов баллов испытуемых по каждому заданию (∑ Х ²), сумма квадратов баллов испытуемых по всему опроснику (∑ Y ²), сумма произведения баллов по каждому заданию и по всем заданиям (∑ XY). Путем подстановки в формулу значений перечисленных показателей вычисляется коэффициент корреляции. Нижеследующий пример демонстрирует простой способ получения этого коэффициента. Для избежания ошибок рекомендуется повторный подсчет по каждому заданию.

При решении вопроса о включении задания в окончательную версию теста нужно принимать во внимание многие факторы. В дополнение к изучению эффективности и дискриминантности нужно определить то количество заданий, которое потребуется для окончательной версии (не менее 20-30 заданий!) и насколько хорошо они "вписываются" в ранее созданную для теста решетку. Например, можно включить задания с низкой дискриминативностью, если имеется немного заданий по некоторой области измерения. Также иногда имеет смысл включение в окончательный вариант опросника задания с недостаточно высоким показателем эффективности при условии, что оно обладает достаточной дискриминантностью. Также важно обеспечить приблизительно равное количество прямых и обратных заданий. Для испытуемых разных полов необходимо выполнить отдельные процедуры анализа заданий.

Испытуемые n	Балл по заданию X	Балл по заданию в квадрате X^2	Балл по всему тесту Y	Бал по всему тесту в квадрате Y^2	Произведение баллов по заданию и по всему тесту XY
n = 10	∑ Х = 30	∑ Х ^2 = 110	∑ Y = 641	∑ Y ^2 = 45195	∑ XY = 2191

r =

10 (2191) - (30) (641)

√[ 110 - (30)² ][ 10 (45195) - (641)²]

.

Способы улучшения заданий выясняются как раз на этой стадии конструирования теста. Например, изменение формулировки ответа в задании с "иногда" на "всегда" может повысить показатель эффективности. Однако эти изменения во всех вопросах (утверждениях) могут повлиять на надежность и валидность теста. Процедура анализа заданий дает необходимую информацию относительно параметров каждого задания. Тем не менее только исследователь может вынести решение о том, какой из критериев наиболее важен для реализации цели создаваемого теста.

В начале 1980-х гг., помимо традиционных процедур анализа заданий, появляются более сложные, использование которых невозможно без достаточно мощного компьютерного обеспечения. К таковым прежде всего относится теория "задание - ответ" (item response theory, IRT). Технические приемы этой теории, несмотря на продолжающиеся дискуссии, сегодня включаются во вновь создаваемые

тесты. Однако речь идет прежде всего о тестировании способностей. Наиболее сложные проблемы возникают в связи с попытками приложения ITR к тестам личности. Безусловно, нельзя утверждать, что процедуры из ITR неприменимы в оценке личности, однако требуется решение многих задач, прежде чем эта теория заменит традиционные процедуры анализа заданий (подробнее об этой теории см. в работах П. Клайна, 1994; А. Анастази и С. Урбина, 2001; и др.).

¹ В ряде случаев определяется как индекс сложности задания; например, во многих шкалах интеллекта присутствуют субтесты, предназначенные для определения общей осведомленности и состоящие из вопросов типа: "Назовите столицу Уругвая" или "Кто автор "Критики чистого разума"?". В таких тестах с помощью индекса сложности устраняются те задания, на которые отвечают почти все испытуемые (легкие) и те, на которые отвечают правильно очень немногие (сложные).

3.6. Определение надежности теста

Тест обычно считается надежным, если с его помощью получаются одни и те же показатели для каждого обследуемого при повторном тестировании.

В психометрике термин надежность имеет два значения. На одном из них - надежности по внутренней согласованности - мы не будем останавливаться подробно, отсылая читателя к соответствующим справочникам и руководствам¹, отметив только, что требование к внутренней согласованности теста не случайно. Вполне естественно считать, что если некоторая переменная измеряется частью теста, то другие его части, не будучи согласованными с первой, измеряют нечто другое. Для того чтобы быть валидным, тест должен быть согласованным. Существует несколько способов определения надежности.

Надежность ретестовая - предполагает повторное предъявление того же самого теста тем же испытуемым и примерно в тех же условиях, что первоначальное, а затем установление корреляции между двумя рядами данных. При использовании этого способа определения надежности нужно отдавать себе отчет в том, что испытуемые могут запомнить свои ответы и воспроизвести их во второй раз, поэтому повторное тестирование должно быть отделено от первого более-менее значительным временным интервалом, обычно не менее месяца. Некоторые психологи настаивают на интервале между тестированиями не менее 6 месяцев (Клайн, 1994).

Мы не считаем требование П. Клайна об обязательном 6 месячном интервале между тестированиями безусловным. В подтверждение сошлемся на результаты исследования канадских психологов. С помощью личностного опросника были обследованы 302 студента с интервалом в 3 недели. Условия повторного тестирования варьировались. Стандартный коэффициент ретестовой надежности, равный 0,872, не отличался от коэффициентов надежности, полученных в трех группах испытуемых, получавших одну из трех специфических инструкций: 1) продумывать ответы; 2) использовать воспоминания о прошлых ответах; 3) выполнять параллельную форму теста. Было обнаружено, что стандартный коэффициент надежности выше коэффициента, полученного при инструкции воспроизводить прошлые ответы.

Наименьшим удовлетворительным значением для ретестовой надежности является коэффициент корреляции, равный 0,7. Правда, для некоторых тестов этот показатель может быть несколько ниже.

Надежность параллельных форм предусматривает создание эквивалентных форм опросника и предъявление их одним и тем же испытуемым для того, чтобы затем оценить корреляцию между полученными результатами. Основная проблема, препятствующая широкому распространению этого способа определения надежности, - необходимость подготовки двух наборов заданий, что чрезвычайно сложно, поскольку требуются убедительные доказательства их эквивалентности.

Надежность частей теста определяется путем деления опросника на две части (обычно на четные и нечетные задания), после чего и рассчитывается корреляция между этими частями. Обычно к этому способу определения надежности рекомендуется прибегать только в тех случаях, когда необходимо быстро получить результаты.

Для определения ретестовой надежности и надежности параллельных форм корреляции подсчитывается на основе коэффициента произведения моментов Пирсона. Эта процедура подсчета рассматривалась нами ранее, в разделе, посвященном анализу заданий. Для определения надежности частей теста ранее рассчитанный коэффициент произведения моментов Пирсона (между двумя половинами теста) используется в формуле Спирмена - Брауна. Формула Спирмена - Брауна имеет вид:

r ₁₁ =

2 r _½½

1 + r _½½

,

где r ₁₁ - надежность, оцененная для всего опросника; r _½½ - корреляция между двумя половинами опросника.

Например, если коэффициент корреляции произведения моментов Пирсона между двумя половинами теста равен 0,80, то:

r ₁₁ =

2 (0,80)

1 + 0,80

= 0,88.

Подчеркнем, что наилучшей процедурой определения надежности является проведение повторных исследований через более или менее значительные временные интервалы.

Все исследования надежности должны выполняться на достаточно больших (рекомендуется 200 и более испытуемых) и репрезентативных выборках. Надежность - важная характеристика теста, но сама по себе ценности не представляет. Она необходима для достижения валидности.

¹ Изданный под нашей редакцией перевод с английского книги П. Клайна "Справочное руководство по конструированию тестов" (Киев, 1994), пока, к сожалению, единственная на русском языке достаточно подробная работа по конструированию тестов, может удовлетворить интерес читателя к этой проблеме.

3.7. Факторный анализ

Во многих случаях перед разработчиком теста встает задача "сжатия" информации или, иначе говоря, компактного описания изучаемых явлений при наличии множества наблюдений или переменных. Факторный анализ как раз и является методом снижения размерности изучаемого многомерного явления.

Напомним читателю, что факторный анализ зародился в психологической науке и связан в первую очередь с исследованиями Ч. Спирмена (Spearman, 1904). Последующими работами таких выдающихся психологов, как Т. Келли, Л. Терстоуна,

Дж. Гилфорда и Р. Кэттелла, а также математиков К. Пирсона, К. Холзингера, Г. Хармана и др., был достигнут значительный успех в математическом обосновании факторного анализа, и этот метод начинает активно применяться в различных науках.

Как хорошо известно, одной из типичных форм представления экспериментальных данных является матрица, столбцы которой соответствуют, например, различным тестам (заданиям тестов), а строки - отдельным результатам (значениям), полученным в результате их применения. Визуальный анализ сколь-нибудь значительной по величине матрицы невозможен, а поэтому требуется исходную информацию сжать, извлечь из нее наиболее важное, существенное. Прежде всего исследователю необходимо получить корреляционную матрицу (подсчет коэффициентов корреляции).

Воспользуемся в качестве примера исследованием Л. Айкена (Aiken, 1996). В этом исследовании 90 студентов колледжа просили оценить преподавателя с помощью пятибалльной шкалы (1 - низший балл, 5 - высший) по 11 параметрам: тактичность, вежливость, креативность, доброжелательность, увлеченность своим предметом, знание предмета, способность мотивировать студентов, организованность, терпеливость, подготовленность и пунктуальность.

Если поделить матрицу корреляций рейтинговых оценок, данных студентами по списку качеств личности преподавателя (табл. 3.4) на два равных треугольника, проведя диагональ из левого верхнего угла в правый нижний угол, то можно увидеть, что это - симметричная матрица, в которой первая верхняя строка состоит из тех же оценок, что и первая колонка. Аналогично вторая строка включает те же самые элементы, что и вторая колонка, и т. д. Также нужно обратить внимание на то, что все числа на основной диагонали (начиная сверху слева вплоть до чисел внизу справа) равны +1,00 - это предполагаемая корреляция каждого задания шкалы с самим собой.

В психологическом тестировании цель факторного анализа заключается в том, чтобы найти несколько фундаментальных факторов, которые объясняли бы большую часть дисперсии в группе оценок по различным тестам или другим психометрическим измерениям. В вышерассмотренном примере - 11 переменных, поэтому для него задача факторного анализа заключается в том, чтобы найти матрицу факторных нагрузок или корреляции между факторами и заданиями шкалы. Существует несколько процедур факторного анализа, но все они предполагают две стадии: 1) факторизацию матрицы корреляций, с тем чтобы получилась первоначальная факторная матрица; 2) вращение факторной матрицы, с тем чтобы обнаружить наиболее простую конфигурацию факторных нагрузок (см. табл. 3.4).

Стадия факторизации в этом процессе призвана определить количество факторов, необходимых для объяснения связей между различными тестами, и обеспечивает получение первичных оценок нагрузки (веса) каждого теста по каждому фактору. Вращение факторов необходимо для того, чтобы сделать их более понятными (интерпретируемыми) с помощью создания конфигурации факторов, в которой совсем немного тестов имеют высокие нагрузки, тогда как большая часть тестов имеют низкие нагрузки по любому фактору.

Таблица 3.4

Образец матрицы корреляций между 11 заданиями шкалы
для оценки личности преподавателя

Задание
	1,000	0,727	0,424	0,573	0,343	0,294	0,458	0,200	0,425	0,091	0,078
	0,727	1,000	0,304	0,620	0,287	0,258	0,363	0,075	0,459	0,115	0,127
	0,424	0,304	1,000	0,470	0,510	0,080	0,691	0,206	0,304	0,129	0,112
	0,573	0,620	0,470	1,000	0,336	0,195	0,390	0,061	0,528	0,026	0,022
	0,343	0,287	0,510	0,336	1,000	0,171	0,638	0,374	0,203	0,243	0,244
	0,294	0,258	0,080	0,195	0,171	1,000	0,108	0,227	0,159	0,490	0,430
	0,458	0,363	0,691	0,390	0,638	0,108	1,000	0,218	0,314	0,108	0,065
	0,200	0,075	0,206	0,061	0,374	0,227	0,218	1,000	00,85	0,524	0,421
	0,425	0,459	0,304	0,528	0,203	0,159	0,314	0,085	1,000	0,114	0,187
	0,091	0,115	0,129	0,026	0,243	0,490	0,108	0,524	0,114	1,000	0,611
	00,78	0,127	0,112	0,022	0,244	0,430	0,065	0,421	0,187	0,611	1,000

Одна из наиболее известных процедур факторизации - метод главных осей (principal cuds), а самая популярная процедура вращения - варимакс вращение ¹.

Из табл. 3.5 видно, что выделяются три фактора, они представлены в колонках, обозначенных Л, В, С. Величины, записанные под колонкой каждого фактора, - корреляции или нагрузки каждого из 11 заданий по этому фактору.

Например, задание 1 имеет нагрузку по фактору Л равную 0,754; - 0,271 по фактору В; и 0,250 по фактору С. Сумма квадратов нагрузок по каждому из факторов позволяет определить долю дисперсии этого задания. Таким образом, доля дисперсии задания 1 равна:

(0,754)² + (- 0,271)² + (0,250)² = 0,704.

Это означает, что 70,4 % вариаций показателей по заданию 1 объясняется действием этих трех факторов.

Факторно-аналитический подход позволяет также оценить надежность теста. Как известно, полная дисперсия теста равна сумме дисперсий для общих факторов, плюс дисперсии специфических факторов, плюс дисперсия погрешности. Следовательно, если мы осуществим факторный анализ теста, возведем в квадрат и суммируем нагрузки его факторов, то мы получим его надежность, поскольку нагрузки факторов представляют корреляцию теста с общими или специфическими факторами. Однако следует помнить, что такой способ установления надежности более всего подходит для уже факторизованного теста, нежели для тестов, которые могут измерять широкий набор разных факторов, часть которых могут и не входить в батарею изучаемых исследователем.

Таблица 3.5

Матрица факторных весов с вращением и без вращения рейтинговых оценок по шкале оценки личности преподавателя (данные получены с помощью программы SPSS ¹)

Задание	Факторные веса	Доля дисперсии
Матрица до вращения	Матрица после вращения
А	В	С	А'	В'	С'
	0,754	-0,271	0,250	0,783	0,090	0,288	0,704
	0,708	-0,281	0,415	0,853	0,089	0,131	0,752
	0,689	-0,206	-0,440	0,303	0,015	0,786	0,710
	0,702	-0,392	0,240	0,790	-0,041	0,280	0,704
	0,674	0,063	-0,500	0,148	0,243	0,792	0,708
	0,442	0,477	0,402	0,353	0,669	-0,113	0,585
	0,714	-0,216	-0,485	0,298	0,009	0,838	0,791
	0,434	0,573	-0,257	-0,082	0,649	0,392	0,582
	0,594	-0,201	0,330	0,691	0,102	0,120	0,502
	0,408	0,769	0,063	0,011	0,867	0,100	0,762
	0,388	0,718	0,122	0,052	0,822	0,048	0,681

Факторная матрица после вращения представлена в колонках A', В' и С'таблицы. Доля дисперсии каждого задания та же самая, что и в факторной матрице до вращения факторов, но факторы, полученные после вращения, легче интерпретировать, чем в матрице до вращения. Вращение варимакс является процедурой ортогонального вращения, в которой факторные оси остаются перпендикулярными друг к другу. В противоположность этой процедуре факторные оси при облическом (косоугольном) вращении формируют острые или тупые углы по отношению друг к другу. Ортогональные факторы обычно легче интерпретировать, чем косоугольные, поскольку эти факторы не коррелируют друг с другом (независимы).

При интерпретации факторной матрицы после вращения следует обратить особое внимание на задания, которые имеют вес 0,50 и выше по данному фактору. Четыре задания - 1 (тактичный), 2 (вежливый), 4 (доброжелательный) и 9 (терпеливый) - имеют высокие нагрузки по фактору А'. Соответственно подходящим названием для этого фактора могло бы быть такое обозначение, как "деликатность" или "вежливость". Еще четыре задания имеют высокие нагрузки, но уже по фактору В': 6 (осведомленный), 8 (организованный), 10 (подготовленный) и 11 (пунктуальный), значит, соответствующим наименованием фактора В' могло бы быть "готовность". Наконец, три задания имеют высокие нагрузки по фактору С': 3 (креативный), 5 (увлеченный) и 7 (способный мотивировать); подходящим обозначением этого фактора могло бы быть - "стимулирующий" или "мотивирующий". Эти три фактора приобретают психологический смысл при определении типа личности преподавателя, который предпочитают студенты.

Безусловно, имеется гораздо больше приложений для факторного анализа, чем те, на которых мы остановились. Сегодня факторному анализу посвящено множество книг и статей. В то же время существуют значительные разногласия не только относительно наилучших процедур факторизации и вращения факторов, но и в отношении их интерпретации. Тем не менее факторный анализ был и остается одним из наиболее мощных инструментов психолога, разрабатывающего тесты.

¹ По вполне понятным причинам здесь опущены этапы ручной факторизации матрицы, поскольку в настоящее время для этой цели используются различные компьютерные программы. Для читателя, желающего ознакомиться подробно с процедурой факторизации матрицы и ее вращением, рекомендуем обратиться к книге: Окунь Я. Факторный анализ / Пер. с польск.; Под ред. Г. 3. Давидовича. - М.: Статистика, 1974.

¹ SРSS - Статистический пакет для социальных наук (Statistical Package for the Social Sciences).

3.8. Валидность теста

Существует достаточно много разных способов доказательства валидности теста. О них и пойдет речь далее.

Тест называется валидным, если он измеряет то, для измерения чего предназначен.

Очевидная валидность - описывает представление о тесте, сложившееся у испытуемого. Тест должен восприниматься обследуемым как серьезный инструмент познания его личности, чем-то схожий с вызывающим уважение и в какой-то мере трепет медицинским диагностическим инструментарием. Очевидная валидность приобретает особое значение в современных условиях, когда представление о тестах в общественном сознании формируется многочисленными публикациями в популярных газетах и журналах того, что можно назвать квазитестами, с помощью которых читателю предлагается определить все, что угодно: от интеллекта до совместимости с будущим супругом.

Конкурентная валидность оценивается по корреляции разработанного теста с другими, валидность которых относительно измеряемого параметра установлена. П. Клайн отмечает, что данные о конкурентной валидности полезны тогда, когда есть неудовлетворительно работающие тесты для измерения некоторых переменных, а новые создаются для того, чтобы улучшить качество измерения. В самом деле, если уже существует эффективный тест, то для чего нужен такой же новый?

Прогностическая валидность устанавливается с помощью корреляции между показателями теста и некоторым критерием, характеризующим измеряемое свойство, но в более позднее время. Например, прогностическая валидность какого- либо теста интеллекта может быть показана корреляцией его показателей, полученных у испытуемого в возрасте 10 лет, с академической успеваемостью в период окончания средней школы. Л. Кронбах считает прогностическую валидность наиболее убедительным доказательством того, что тест измеряет именно то, для чего он был предназначен. Основная проблема, с которой сталкивается исследователь, пытающийся установить прогностическую валидность своего теста, состоит в выборе внешнего критерия. В особенной степени чаще всего это касается измерения личностных переменных, где подбор внешнего критерия - чрезвычайно сложная задача, решение которой требует немалой изобретательности. Несколько проще обстоит дело при определении внешнего критерия для когнитивных тестов, однако и в этом случае исследователю приходится "закрывать глаза" на многие проблемы. Так, академическая успеваемость традиционно используется в качестве внешнего критерия при валидизации тестов интеллекта, но в то же

время хорошо известно, что успехи в обучении далеко не единственное свидетельство высокого интеллекта.

Инкрементная валидность имеет ограниченное значение и относится к случаю, когда один тест из батареи тестов может иметь низкую корреляцию с критерием, но не перекрываться другими тестами из этой батареи. В этом случае данный тест обладает инкрементной валидностью. Это может быть полезно при проведении профотбора с помощью психологических тестов.

Дифференциальная валидность может быть проиллюстрирована на примере тестов интересов. Тесты интересов обычно коррелируют с академической успеваемостью, но по-разному для разных дисциплин. Значение дифференциальной валидности, так же как и инкрементной, ограничено.

Содержательная валидность определяется через подтверждение того, что задания теста отражают все аспекты изучаемой области поведения. Обычно она определяется у тестов достижений (смысл измеряемого параметра полностью ясен!), которые, как уже указывалось, тестами собственно психологическими не являются. На практике для определения содержательной валидности подбираются эксперты, которые указывают, какая область (области) поведения наиболее важна, например, для музыкальных способностей, а затем, исходя из этого, генерируются задания теста, которые вновь оценивают эксперты.

Конструктная валидность теста демонстрируется полным, насколько это возможно, описанием переменной, для измерения которой предназначается тест. По сути дела, конструктная валидность включает в себя все подходы к определению валидности, которые были перечислены выше. Кронбах и Мил (Cronbach & Meehl, 1955), которые ввели в психодиагностику понятие конструктной валидности, пытались решить проблему отбора критериев при валидизации теста. Они подчеркивали, что во многих случаях ни один отдельно взятый критерий не может служить для валидизации отдельного теста. Можно считать, что решение вопроса о конструктной валидности теста представляет собой поиск ответа на два вопроса: 1) существует ли реально некоторое свойство; 2) надежно ли измеряет данный тест индивидуальные различия по этому свойству. Вполне понятно, что с конструктной валидностью связана проблема объективности в интерпретации результатов по изучению конструктной валидности, однако эта проблема общепсихологическая и выходит за рамки валидности (подробнее см. гл. 2).

Из вышесказанного следует, что не существует какого-либо единичного показателя, с помощью которого устанавливается валидность психологического теста. В отличие от показателей надежности и дискриминативности, нельзя осуществить точные статистические расчеты, подтверждающие валидность методики. Тем не менее разработчик должен представить весомые доказательства в пользу валидности теста, что потребует от него психологических знаний и интуиции.

3.9. Стандартизация теста

Одним из важных отличий психометрических тестов является то, что они стандартизированы, а это позволяет сравнить показатели, полученные одним испытуемым, с таковыми в генеральной совокупности или соответствующих группах.

Тем самым достигается адекватная интерпретация показателя отдельного испытуемого. Таким образом, стандартизация теста наиболее важна в тех случаях, когда осуществляется сравнение показателей обследуемых. При этом вводится понятие нормы, или нормативных показателей. Для получения стандартных норм нужно тщательно отобрать большее количество испытуемых в соответствии с ясно обозначенным критерием. При формировании выборки стандартизации следует учитывать ее объем и репрезентативность. В руководствах по тестам чаще всего указывается на то, что для простого уменьшения стандартной погрешности достаточной будет выборка из 500 испытуемых. Однако репрезентативность выборки не зависит от ее объема. Например, для того чтобы получить нормативные показатели для всей популяции детей, обучающихся в начальной школе, потребуется выборка объемом более 10 тысяч, тогда как выборка из такой ограниченной популяции, как шеф-пилоты авиакомпаний, не может быть столь значительной. Репрезентативность выборки, таким образом, параметр более важный, нежели ее объем. В некоторых случаях приходится формировать несколько групп стандартизации или стратифицировать группу стандартизации относительно таких параметров, как возраст, пол, социальный статус. Устанавливать нормы не всегда обязательно. При использовании психологических тестов в научном исследовании нормы не столь важны и достаточно "сырых" показателей теста.

Нормы для каждой группы должны быть представлены в средних величинах и показателе стандартного отклонения. Расчет средней величины элементарен и хорошо известен, а стандартное отклонение определяется с помощью формулы, имеющей вид:

SD = √

n ∑ X ² - (∑ X)²

n (n - 1)

,

где SD - стандартное отклонение; X ² - результат всего опросника всех испытуемых; n - количество испытуемых; ∑ - сумма.

Сегодня на практике все больше используется такой тип производной оценки, как стандартные показатели, удовлетворяющий большинству требований, предъявляемых к психологическому измерению. Такие показатели выражают отличие индивидуального результата испытуемого от среднего в единицах стандартного отклонения соответствующего распределения. Стандартные показатели получают двумя путями: линейным и нелинейным преобразованием первичных ("сырых") оценок. В случае линейного преобразования сохраняются все свойства исходного распределения "сырых" оценок, и такие показатели называются стандартными или 2-показателями. Для вычисления z-показателя находят разность между первичной оценкой и средним для нормативной группы и делят ее на стандартное отклонение нормативной группы. Формула имеет вид:

z =

X - X

SD

.

Здесь необходимо сказать о том, что основной причиной преобразования первичных оценок в некоторую производную шкалу является желание получить показатели, которые сопоставимы между собой вне зависимости от того, по какому

тесту они получены. Линейное преобразование позволяет получить показатели сопоставимые лишь в том случае, когда распределения "сырых" оценок, по которым они рассчитываются, имеют примерно одинаковую форму. Для того чтобы сопоставлять показатели, полученные на основе распределений разной формы, прибегают к нелинейному преобразованию, или к нормализованным стандартным показателям. Процедура нелинейного преобразования достаточно проста и описана в многочисленных руководствах по математической статистике. Такие показатели обычно рассчитывают с помощью таблиц. В этих таблицах приводится процент случаев, приходящихся на участки, которые отстоят от среднего нормальной кривой на некоторое число единиц стандартного отклонения. Сначала определяют процент лиц, чьи показатели превышают каждую "сырую" оценку, а затем по этому проценту в таблице отыскивают соответствующее значение нормализованного стандартного показателя. Эти показатели, как и линейно преобразованные, будут иметь среднее (X), равное 0, и стандартное отклонение (SD), равное 1. Нулевое значение показывает, что испытуемый попадает в точку, соответствующую среднему нормальной кривой, превосходя 50 % группы. В случае, если показатель равен - 1, испытуемый превосходит примерно 16 % группы, а если +1 - превосходит 84 % группы. Нормализованным стандартным показателям можно придать любую удобную форму, например, умножив его на 10 и прибавив произведение к 50, получаем так называемый " Т -показатель" и в этом случае Т, равное 50, соответствует среднему, равному 60 - превышает среднее на одно стандартное отклонение и т. д. С другими, не менее популярными нелинейными преобразованиями "сырых" показателей теста, можно ознакомиться в соответствующей литературе¹.

Созданием стандартизованного теста и его публикацией обычно завершается работа психолога, однако следует помнить и о том, что с течением времени необходим пересмотр (ревизия) теста. Достаточно вспомнить о тестах интеллекта (см. гл. 4), нормы по которым устаревают через каждые 5 лет, и можно предположить, что процесс их старения будет ускоряться. Для наглядности этапы конструирования теста представлены на рис. 3.1.

Пример из практики: определение надежности опросника 16 PF Кеттелла. Личностный опросник Раймонда Кеттелла 16 PF (16 личностных факторов) относится к наиболее распространенным психодиагностическим инструментам и не нуждается в специальном представлении. Уже без малого 50 лет психологи всего мира используют его для решения разнообразных прикладных и научных задач. Однако как в бывшем СССР, так и ныне во вновь образованных странах этот опросник, несмотря на достаточно большую популярность, используется непрофессионально, с нарушением всех норм и правил, предъявляемых к психологическим тестам.

Кроме различных переводов опросника, которые существенно отличаются один от другого, в русскоязычной литературе часто встречаются и различные

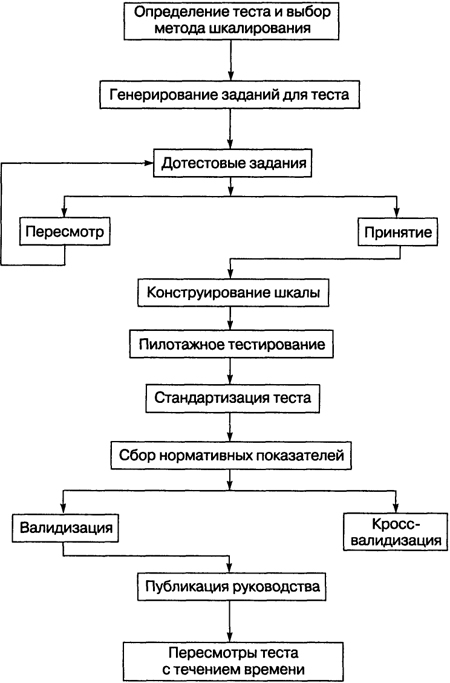
Рис. 3.1. Этапы конструирования теста

"ключи" к его факторам. Опубликованные в многочисленных сборниках и брошюрах варианты опросника не защищены (!) от ошибок и произвольного вмешательства в его текст. Если добавить к этому отсутствие нормативных данных, а также то, что не проводилась проверка гомогенности шкал опросника на отечественных выборках, то непонятно, какого рода результаты получали его многочисленные пользователи, какими диагностическими заключениями они оперировали. За последние пятнадцать лет у нас появились только три (!) работы, в которых ставилась задача проверки факторной структуры 16 PF нa национальных выборках:

это статьи В. М. Русалова и О. В. Гусевой (1990), Ю. М. Забродина, В. И. Похилько и А. Г. Шмелева (1987), наконец, украинского психолога А. Г. Виноградова (1997). Читателю нетрудно сравнить это количество публикаций с тем множеством работ, в которых опросник использовался для получения "диагностически значимых результатов". Сказанное позволяет сделать вывод о том, что с помощью опросника 16PF измеряется нечто, имеющее неясное отношение к факторам личности, выделенным и описанным Кеттеллом.

Занимаясь работой по психометрической адаптации личностных опросников¹, мы не могли обойти вниманием и столь широко распространенный, как 16PF. За основу была взята форма "А" опросника 16 PF. Были обследованы 227 человек (135 женщин и 92 мужчины) в возрасте от 16 до 51 года. Средний возраст исследуемых составлял 28 лет. Это были люди, которые проходили отбор на различные должности в коммерческие организации Киева, все они имели высшее или среднее специальное образование (бухгалтеры, коммерческие директоры, менеджеры разного уровня).

Как известно, точность измерения с помощью психодиагностического инструмента определяется его надежностью. С целью выяснить, насколько точен прогноз, даваемый психологом на основании результатов 16 PF, данные, первоначально полученные нами, были оценены по авторским ключам на внутреннюю согласованность с помощью коэффициента Кронбаха, вычисляемого по следующей формуле:

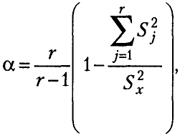
где a - коэффициент Кронбаха; r - количество заданий теста; S ² _j - дисперсия по j -му пункту теста; S ² _x - дисперсия суммарных баллов по всему тесту.

В табл. 3.6 содержатся данные о внутренней согласованности факторов личности, полученные по авторским "ключам" (приведено буквенное обозначение фактора). Как видно из таблицы, значение коэффициента Кронбаха неудовлетворительно для большинства факторов. А фактор N вообще измеряет нечто, не имеющее никакого отношения к проницательности, расчетливости и наивности (если употреблять обыденное название этого фактора). Лишь некоторые из факторов, например фактор F (сургенция - десургенция) и фактор H пармия - тректия (смелость - робость), надежно измеряют то, что должны измерять. Таким образом, в результате проверки надежности - согласованности оригинальных ключей было показано, что ряд шкал опросника негомогенны. Можно предположить, что это следствия искажения смысла заданий при переводе на русский язык и/или существования известных культурных различий.

Для того чтобы выявить, что же именно стоит за данными, получаемыми с помощью 16 PF, мы использовали факторный анализ. Факторы извлекались методом

Таблица 3.6

Дата добавления: 2015-06-04