
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи контрольной работы
|
|
|
|
Задача С1
Жёсткая рама, расположенная в вертикальной плоскости (рис. 0 – 9, табл. С1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р= 25 кН. На раму действуют пара сил с моментом М= 50 кН·м, равномерно распределенная нагрузка интенсивности  кН/м, которая действует на участке, указанном для каждого рисунка и сила
кН/м, которая действует на участке, указанном для каждого рисунка и сила  , модуль, точка приложения и направление которой указаны в таблице С1; в окончательных расчётах принять a= 0,5 м. Направление действия распределённой нагрузки:
, модуль, точка приложения и направление которой указаны в таблице С1; в окончательных расчётах принять a= 0,5 м. Направление действия распределённой нагрузки:
| горизонтальный участок | вертикальный участок |

| 
|
Определить реакции связей в точках А, В, вызываемые действующими нагрузками.
Указания. Задача С1 – на равновесие тела под действием произвольной плоской системы сил. При её решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы  удобно разложить её на составляющие
удобно разложить её на составляющие  и
и  , для которых плечи легко определя-ются, и воспользоваться теоремой Вариньона:
, для которых плечи легко определя-ются, и воспользоваться теоремой Вариньона:  . Если в результате решения задачи знак алгебраической величины какой-либо силы оказывается отрицательным, то это означает, что ее направление противоположно первоначально выбранному на чертеже. Необходимо помнить, что по закону действия и противодействия давление данного тела на связь равно по величине и противоположно по направлению реакции связи.
. Если в результате решения задачи знак алгебраической величины какой-либо силы оказывается отрицательным, то это означает, что ее направление противоположно первоначально выбранному на чертеже. Необходимо помнить, что по закону действия и противодействия давление данного тела на связь равно по величине и противоположно по направлению реакции связи.
Пример С1. Дано:  =25 кН,
=25 кН, 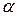 =60°,
=60°,  =18 кН,
=18 кН, 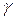 =75°,
=75°,  =50 кН·м,
=50 кН·м,  =2 кН/м,
=2 кН/м, 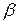 =30°,
=30°,  =0,5 м (рис. С1).
=0,5 м (рис. С1).
Определить реакции в точках  ,
,  , вызываемые действующими нагрузками.
, вызываемые действующими нагрузками.
Решение. Рассмотрим равновесие рамы. Проведём координатные оси xy и изобразим действующие на раму силовые факторы: силу  , пару сил с моментом М, натяжение троса
, пару сил с моментом М, натяжение троса  (по модулю Т=Р), реакции связей
(по модулю Т=Р), реакции связей  (реакцию неподвижной шарнирной опоры А изображаем двумя её составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости); равномерно распределенную нагрузку интенсивности
(реакцию неподвижной шарнирной опоры А изображаем двумя её составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости); равномерно распределенную нагрузку интенсивности  , действующую на участке
, действующую на участке  , заменяем сосредоточенной силой
, заменяем сосредоточенной силой  (по модулю
(по модулю  =2 кН), которая приложена посередине участка.
=2 кН), которая приложена посередине участка.
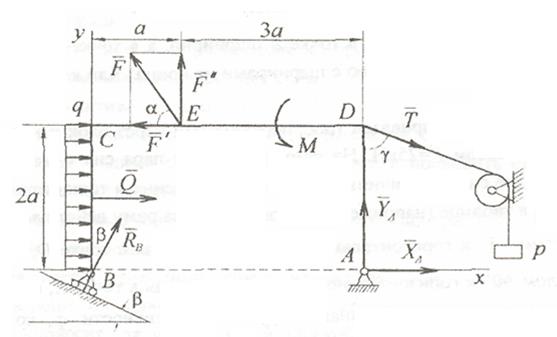
Рис. С1
Для равновесия данной плоской системы сил необходимо и достаточно выполнения трёх уравнений: суммы проекций всех сил на координатные оси x и y, а также сумма их моментов относительно любого центра равны нулю. В третьем уравнении при вычислении момента силы  относительно точки А воспользуемся теоремой Вариньона, т. е. разложим силу
относительно точки А воспользуемся теоремой Вариньона, т. е. разложим силу  на составляющие
на составляющие  ,
,  (
( ,
,  ) и учтём, что
) и учтём, что  . Получим:
. Получим:





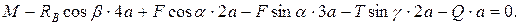
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Ответ:  кН;
кН;  кН;
кН;  кН. Знаки указывают, что силы
кН. Знаки указывают, что силы  и
и  направлены противоположно показанному на рис. С1.
направлены противоположно показанному на рис. С1.
Выполним проверку решения. Для этого составим еще одно дополнительное уравнение моментов относительно такой точки, чтобы в уравнение вошли найденные реакции  . Например, в качестве проверочного можно записать уравнение моментов относительно точки
. Например, в качестве проверочного можно записать уравнение моментов относительно точки  :
:

 .
.
При указанных значениях  последнее уравнение равно нулю с точностью до третьего знака после запятой (погрешность зависит от ошибки, с которой вычислялись искомые реакции), следовательно, задача решена верно.
последнее уравнение равно нулю с точностью до третьего знака после запятой (погрешность зависит от ошибки, с которой вычислялись искомые реакции), следовательно, задача решена верно.
Таблица С1
| Номер условия | |||||||||||
Сила

| модуль кН | ||||||||||
| точка прилож. | K | H | E | K | H | D | K | H | E | K | |

| |||||||||||
| направ-ление | 
| 
| 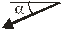
| 
|
 Рис. 0 (q на отрезке СЕ) Рис. 1 (q на отрезке KЕ)
Рис. 0 (q на отрезке СЕ) Рис. 1 (q на отрезке KЕ)
 Рис. 2 (q на отрезке СН) Рис. 3 (q на отрезке KС)
Рис. 2 (q на отрезке СН) Рис. 3 (q на отрезке KС)
Задача С2
Плоская ферма, расположенная в вертикальной плоскости, закреплена в точках А и В, причём в одной из них шарнирно-неподвижно, а в другой опирается на подвижный шарнир (рис. 0 – 9). К ферме приложена наклонная сила  , для которой модуль и угол
, для которой модуль и угол 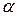 указаны в таблице С2, горизонтальная сила
указаны в таблице С2, горизонтальная сила  и вертикальная
и вертикальная  ; в расчётах принять Q = 5 кН, Р = 20 кН, a =3 м.
; в расчётах принять Q = 5 кН, Р = 20 кН, a =3 м.
Определить опорные реакции в точках А и В, усилия в стержнях 1, 2, 3, 4 методом вырезания узлов, а в стержнях 5, 6, 7 – методом сквозных сечений (Риттера).
Указания. Задача С2 – на расчёт плоской фермы, который сводится к определению опорных реакций и усилий в её стержнях. Опорные реакции можно найти обычными методами статики из 3-х уравнений равновесия, рассматривая ферму в целом как твёрдое тело.
При определении усилий в стержнях методом вырезания узлов мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние силы, реакции самих стержней и составляют уравнения равновесия сил, приложенных к каждому узлу:  ,
, 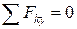 . Условно предполагают, что все стержни растянуты, т.е. реакции стержней направлены от узлов. Если в результате вычислений получен ответ со знаком минус, то это значит, что соответствующий стержень сжат. Последовательность рассмотрения узлов обычно определяется условием: число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия, т.е. двух.
. Условно предполагают, что все стержни растянуты, т.е. реакции стержней направлены от узлов. Если в результате вычислений получен ответ со знаком минус, то это значит, что соответствующий стержень сжат. Последовательность рассмотрения узлов обычно определяется условием: число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия, т.е. двух.
Методом Риттера удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности, для проверочных расчётов. Для определения усилия в каком-нибудь стержне ферму рассекают на две части сечением, проходящем через три стержня, в том числе и через тот, в котором определяется усилие. Одну из частей вместе с приложенными к ней силами мысленно отбрасывают, а её действие заменяют соответствующими силами, направляя их вдоль разрезанных стержней в сторону отброшенной части. Затем составляют уравнения моментов сил, действующих на рассматриваемую часть фермы, относительно точки пересечения двух рассечённых стержней, усилия в которых на данном этапе не определяются. Эта точка пересечения называется точкой Риттера. Если точка Риттера находится в бесконечности, т.е. стержни параллельны, то составляют уравнение суммы проекций сил, приложенных к рассматриваемой части фермы, на ось, перпендикулярную этим параллельным стержням.
Пример С2. Схема фермы, все действующие нагрузки и размеры показаны на рис. С2.1.
Дано: Р =10 кН, F =30 кН.
Определить опорные реакции и усилия в стержнях 1 – 4 методом вырезания узлов, 5 – 7 – методом сквозных сечений.

Рис. С2.1
Решение. При определении опорных реакций ферма рассматривается как твёрдое тело. Опоры в узлах А и В мысленно отбрасываются и заменяются соответствующими реакциями: составляющие  в узле А,
в узле А,  в узле В (рис. С2.2).
в узле В (рис. С2.2).
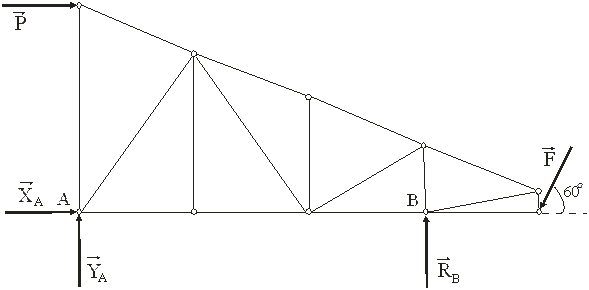
Рис. С2.2
Составляются три уравнения равновесия:



Из первого уравнения ХА= 5 кН, из третьего 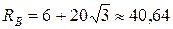 кН, из второго
кН, из второго 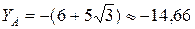 кН; знак «–» показывает, что истинное направление
кН; знак «–» показывает, что истинное направление  противоположно изображённому на рис. С2.2.
противоположно изображённому на рис. С2.2.
Проверка:
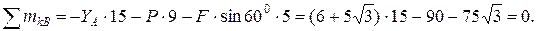
При определении усилий в стержнях 1 – 4 методом вырезания узлов сначала мысленно вырезается узел D (в нём сходятся два стержня, усилия в которых неизвестны), и изображаются все приложенные к нему силы и реакции (рис. С2.3).

Рис. С2.3 Рис. С2.4
По геометрическим размерам фермы (рис. С.2.5) 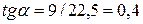 , следовательно,
, следовательно,  ,
,  . Уравнения равновесия имеют вид
. Уравнения равновесия имеют вид

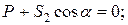
 кН.
кН.

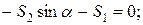
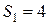 кН.
кН.
Затем вырезается узел А (рис. С2.4), здесь неизвестны усилия 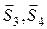 ;
; 




 кН.
кН.

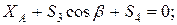
 кН.
кН.
При определении усилий в стержнях 5 – 7 методом Риттера ферма рассекается по этим трём стержням на две части. Одна из частей вместе с приложенными к ней нагрузками мысленно отбрасывается, а её действие на оставшуюся часть заменяется усилиями  , которые направлены вдоль соответствующих стержней в сторону отброшенной части (рис. С2.5).
, которые направлены вдоль соответствующих стержней в сторону отброшенной части (рис. С2.5).
Для определения  составляется уравнение моментов от сил, приложенных к оставшейся части фермы, относительно точки пересечения двух остальных разрезанных стержней (точка L).
составляется уравнение моментов от сил, приложенных к оставшейся части фермы, относительно точки пересечения двух остальных разрезанных стержней (точка L).


 кН.
кН.
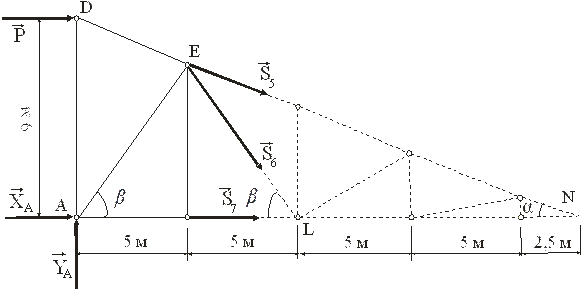
Рис. С2.5
Для определения 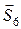 составляется уравнение моментов относительно точки N.
составляется уравнение моментов относительно точки N.


 кН.
кН.
При определении 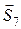 составляется уравнение моментов относительно точки Е.
составляется уравнение моментов относительно точки Е.


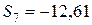 кН.
кН.
Результат  согласуется с леммой 2 о нулевых стержнях [1, §12], что является дополнительной проверкой результатов счёта.
согласуется с леммой 2 о нулевых стержнях [1, §12], что является дополнительной проверкой результатов счёта.
Ответ:  кН;
кН;  кН;
кН;  кН; S1 = 4 кН; S2 = –10,77 кН; S3 = 13,1 кН; S4 = –12,61 кН; S5 = 12,19 кН; S6 = –23,58 кН; S7 = –12,61 кН. Знаки указывают, что сила
кН; S1 = 4 кН; S2 = –10,77 кН; S3 = 13,1 кН; S4 = –12,61 кН; S5 = 12,19 кН; S6 = –23,58 кН; S7 = –12,61 кН. Знаки указывают, что сила  направлена противоположно показанному на рис. С2.2, стержни 2,4,6,7 – сжаты, 1,3,5 – растянуты.
направлена противоположно показанному на рис. С2.2, стержни 2,4,6,7 – сжаты, 1,3,5 – растянуты.
Таблица С2
| Номер условия | ||||||||||
| F, кН | ||||||||||

|
Задача С3
Определить координаты центра тяжести плоской фигуры, изображённой на соответствующем варианту задания рисунке (рис. 0 – 9), с учётом геометрических данных табл. С3.
Указания. Задача относится к теме: определение положения центра тяжести плоских фигур. В решении необходимо применить способ разбиения, при котором плоская фигура разбивается на простейшие части (прямоугольник, треугольник, полукруг), для которых положение центра тяжести известно:
для прямоугольника (квадрата) – на пересечении диагоналей;
для прямоугольного треугольника – в точке пересечения отрезков, проведённых на расстоянии 1/3 длины соответствующего катета ему перпендикулярно от вершины прямого угла;
для полукруга – на оси симметрии полукруга на расстоянии 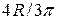 от центра соответствующего круга.
от центра соответствующего круга.
Координаты центра тяжести плоской фигуры определяются по формулам
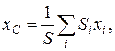
 ,
,
где  – координаты центра тяжести простейшей части фигуры,
– координаты центра тяжести простейшей части фигуры,  – её площадь,
– её площадь, 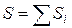 – суммарная площадь.
– суммарная площадь.
Для фигур, имеющих вырезы в виде простейших частей, применяется частный случай способа разбиений – способ дополнения (метод отрицательных площадей).
Пример С3. Определить координаты центра тяжести плоской фигуры, изображённой на рис. С3 при следующих данных: а =40 см, b =100 см, r =20 см.
Решение. Фигура разбивается на три простейшие части: прямоугольник, треугольник, полукруг, площади которых соответственно равны
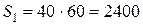 см2,
см2, 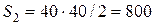 см2,
см2,  см2.
см2.
Площадь всей фигуры
 см2.
см2.

Рис. С3
Центры тяжестей рассматриваемых частей фигуры имеют следующие координаты:
для прямоугольника х 1=30 см, y 1=20 см;
для треугольника х 2=60+40/3=73,3 см, y 2=40/3=13,3 см;
для полукруга х 3=40 см, y 3=40-4·20/(3·π)=31,5 см.
Координаты центра тяжести фигуры в целом вычисляются по формулам
 см;
см;
 см.
см.
Ответ: xC = 41 см, yC = 15,1 см.
Таблица С3
| Номер условия | ||||||||||
| a, см | ||||||||||
| b, см | ||||||||||
| r, см |

|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2241; Нарушение авторских прав?; Мы поможем в написании вашей работы!