Совместное использование и преобразование карт при картографическом методе исследования

Математического моделирования.

Математической статистики.

Используется для исследования явлений, которые можно рассматривать на карте, как однородные множества, изменяющиеся в пространстве, величин. Это статистические совокупности, а в географии – поля (температурные, давления).

Различают: генеральную совокупность и выборку. Генеральная – всё множество точек. Выборка – только часть. Именно по этой части судят о генеральной. Выборка: вручную (палетками), автоматически компьютером (цифрование).

Задачи, решаемые методом:

1. Вычисление обобщенных статистических показателей, с помощью которых можно судить о характере пространственно-временной изменчивости явления.

Показатели: средние значения, различные отклонения от средних значений.

2. Изучение пространственно-временных взаимосвязей между двумя или несколькими явлениями. Для этого используется корреляционный анализ. Коэффициенты корреляции: парный коэффициент корреляции – количественная оценка тесноты связей между двумя явлениями, визуальный коэффициент корреляции.

3. Оценка вклада отдельных факторов в распределение исследуемого явления и выявление ведущих факторов. Факторный анализ.

Это создание по данным, взятым с карт, пространственных математических моделей. Возможность точного анализа обусловлена тем, что многие явления на картах связаны друг с другом функциональными зависимостями. Схема: карта-мат.модель-карты. Самый распространенный прием – составление уравнений поверхности. Суть: замена исходных поверхностей приближенными, которые получаются при их описании известными математическими функциями. В результате исходное изображение раскладывается на составляющие. В графическом отношении это две карты, а в математическом – таблицы. 1 карта – фоновая поверхность, 2 – остаточная. Считают, что ФП показывает зависимость явлений от ведущих факторов, а ОП – вклад менее значимых факторов (аномальных).

Среди различных методов совместного использования карт особенно эффективны 4: 1) совместный анализ карт разной тематики, 2) совместный анализ разновеликих карт, 3) сравнительное изучение карт-аналогов, 4) преобразование карт.

1) позволяет определить прчинно-следственные связи между явлениями. Если они уже известны, то можно получить представление о более сложном явлении, для которого изображенные на карте характеристики, являются характеристиками его состояния.

Картографическая проекция — математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли — эллипсоид, не развертываемый в плоскость, заменяют на другую фигуру, развёртываемую на плоскость, или непосредственно на плоскость. При этом с эллипсоида на другую фигуру переносят сетку параллелей и меридианов. Вид этой сетки бывает разный в зависимости от того, какой фигурой заменяется эллипсоид. В любой проекции существуют искажения, они бывают четырех видов: искажения длин, искажения углов, искажения площадей, искажения форм. Искажение длин означает непостоянство масштаба плоского изображения, что проявляется в изменении масштаба от точки к точке, и даже в одной и той же точке в зависимости от направления. Масштаб: главный, он на карте подписывается, но на самом деле это масштаб исходного эллипсоида, развертыванием которого в плоскость карта и получена; частный масштаб — их бесконечно много на карте, он меняется от точки к точке и даже в пределах одной точки. За характеристику искажения площадей принимают отклонение площади эллипса искажений от исходной площади на эллипсоиде. Искажения формы — графическое изображение вытянутости эллипсоида. Искажения формы — графическое изображение вытянутости эллипсоида.

Уравнения общего вида: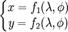

где λ и φ — широта и долгота точки на земном эллипсоиде

Эллипс искажений в картографической проекции - бесконечно малый эллипс в каждой точке на карте, являющийся изображением бесконечно малого круга на поверхности эллипсоида или шара.

Классификация проекций по характеру искажений

Равноугольные проекции — проекции без искажений углов. Весьма удобны для решения навигационных задач. Угол на местности всегда равен углу на карте, линия прямая на местности, прямая на карте. Главным примером данной проекции является поперечно-цилиндрическая Проекция Меркатора (1569 г.) и до сих пор она используется для морских навигационных карт.

В равновеликих проекциях отсутствуют искажения площадей, но при этом сильны искажения углов и форм. (материки в высоких широтах сплющиваются). В такой проекции изображаются экономические, почвенные и другие карты.

В произвольных проекциях имеются искажения и углов, и площадей, но в значительно меньшей степени, чем в равновеликих и равноугольных проекциях, поэтому они наиболее употребляемые.

Цилиндрические проекции - картографические проекции, меридианы которых - равноотстоящие параллельные прямые, а параллели - перпендикулярные им прямые. Применяются для изображения областей, вытянутых вдоль экватора или какой-либо параллели. По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и поперечные цилиндрические проекции в зависимости от расположения изображаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой. Существуют разные способы образования цилиндрических проекций. Наглядным представляется проектирование земной поверхности на боковую поверхность цилиндра, которая затем развертывается на плоскости. Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору, во втором — по двум стандартным параллелям, симметричным относительно экватора.

Конические проекции (нормальные), картографические проекции, в которых параллели изображаются концентрическими окружностями, меридианы - ортогональными им прямыми. В конических проекциях искажения не зависят от долготы. Особо пригодны для территорий, вытянутых вдоль параллелей. По характеру искажений конические проекции могут быть различными. Наибольшее распространение получили равноугольные и равнопромежуточные проекции. Образование конических проекций можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида). В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий. После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость. При проектировании по методу линейной перспективы получаются перспективные конические проекции, обладающие только промежуточными свойствами по характеру искажений.

В зависимости от размеров изображаемой территории в конических проекциях принимаются одна или две параллели, вдоль которых сохраняются длины без искажений. Одна параллель (касательная) принимается при небольшом протяжении по широте; две параллели (секущие) — при большом протяжении для уменьшения уклонений масштабов от единицы.

Азимутальная проекция - картографическая проекция, в которой параллели нормальной сетки есть концентрические окружности, а меридианы - их радиусы, расходящиеся из общего центра параллелей под углами, равными разности долгот.

Нормальные азимутальные проекции применяются для карт полярных стран.

Поперечные и косые азимутальные проекции применяются для карт земных полушарий, материков, звездного неба, Луны и других планет.

Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.

В зависимости от искажений азимутальные проекции подразделяются на равноугольные, равновеликие и с промежуточными свойствами. В проекции масштаб длин может сохраняться в точке или вдоль одной из параллелей (вдоль альмукантарата). В первом случае предполагается касательная картинная плоскость, во втором — секущая. В прямых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных — только для поверхности шара.

Классификация проекция по виду меридианов и параллелей нормальной сетки.

Цилиндрическая. Меридианы и параллели – взаимноперпендикулярные прямые.

Коническая. Параллели – дуги концентрических окружностей, меридианы – азимутальные прямые, выходящие из одного центра.

Азимутальная. Параллели – концентрические окружности, меридианы – радиальные прямые из центра окружностей.

Поликоническая. Параллели - дуги эксцентрических окружностей, меридианы – кривые симметричные относительно прямого центрального меридиана.

Псевдоцилиндрическая. Параллели – параллельные прямые, меридианы – кривые, симметричные относительно центрального меридиана.

Псевдоконическая. Параллели – дуги концентрических окружностей, меридианы – кривые, симметричные относительно прямого центрального меридиана.

Дата добавления: 2015-06-04