Волны де Бройля

Корпускулярно-волновой дуализм свойств частиц.

КВАНТОВАЯ ФИЗИКА И ФИЗИКА АТОМА

Квантовая физика и физика атома.

Результат вычитания вселенной из самой себя.

Задание №1

Задание №2

Задание №3

Задание №4

Задание №5

Задание №6

Задание №7

Задание №8

Задание №9

Задание №10

Задание №11

Задание №12

Задание №13

Задание №14

Задание №15

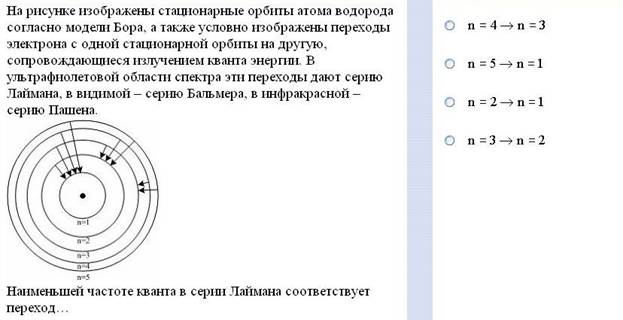
Задание №16

Задание №17

Задание №18

Задание №19

Задание №20

Задание №21

Задание №22

Задание №23

Задание №24

Групповая скорость волны Де Бройля...

*1) равна скорости частицы

2) зависит от квадрата длины волны

3) не имеет смысла как физическая величина

4) равна скорости света в вакууме

5) больше скорости света в вакууме

Кинетическая энергия классической частицы увеличилась в 2 раза. Длина волны Де Бройля этой частицы...

*1) уменьшилась в 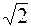раз

2) увеличилась в 2 раза

3) не изменилась

4) увеличилась в 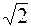раз

5) уменьшилась в 2 раза

Если частицы имеют одинаковую длину волны Де Бройля, то наибольшей скоростью обладает...

*1) позитрон 2) нейтрон 3) протон 4) 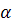-частица

Если частицы движутся с одинаковой скоростью то наименьшей длиной волны Де Бройля обладает...

*1) a-частица 2) нейтрон 3) позитрон 4) протон

Если частицы имеют одинаковую скорость, то наибольшей длиной волны Де Бройля обладает...

*1) электрон 2) нейтрон 3) протон 4) 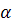-частица

Уравнение Шрёдингера (общие свойства)

Нестационарным уравнением Шредингера является уравнение...

*

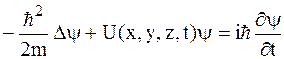
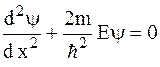
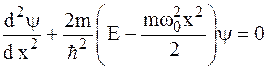
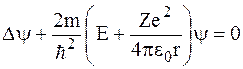
Стационарным уравнением Шредингера для частицы в одномерном ящике с бесконечно высокими стенками является уравнение...

*

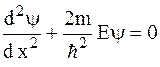
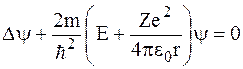
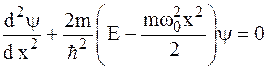
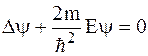
Стационарное уравнение Шредингера в общем случае имеет вид:

,

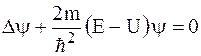где U - потенциальная энергия частицы.

Электрону, движущемуся в одномерной потенциальной яме с бесконечно высокими стенками, соответствует уравнение...

*

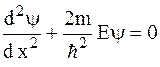
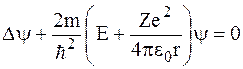
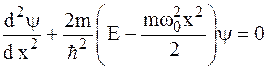
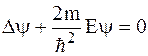
Установите соответствие уравнений Шрёдингера их физическому смыслу

	Нестационарное
	Стационарное для микрочастицы в потенциальной одномерной яме
	Стационарное для электрона в атоме водорода
	Стационарное для гармонического осциллятора

А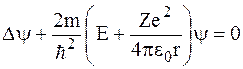
Б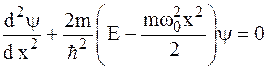
В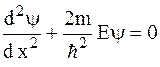
Г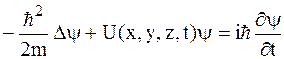
Д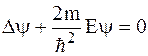

*1-Г, 2-В, 3-А, 4-Б

1-Г, 2-Б, 3-А, 4-В

1-А, 2-Б, 3-Г, 4-В

1-В, 2-Б, 3-А, 4-Д

Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение...

*

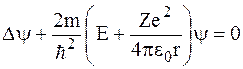
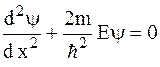
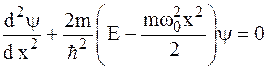
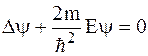
Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение…

*

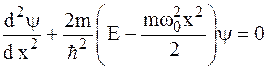
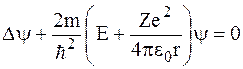
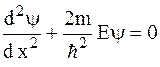
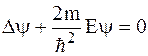
Стационарное уравнение Шредингера в общем случае имеет вид:

,

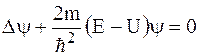где U- потенциальная энергия микрочастицы. Электрону в атоме водорода соответствует уравнение…

*

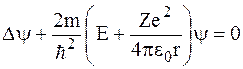
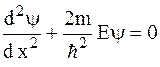
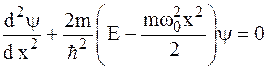
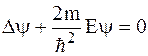
Квадрат модуля волновой функции y, входящей в уравнение Шрёдингера, равен …

*Плотности вероятности обнаружения частицы в соответствующем месте пространства

Импульсу частицы в соответствующем месте пространства

Энергии частицы в соответствующем месте пространства

С помощью волновой функции y, входящей в уравнение Шрёдингера, можно определить …

*С какой вероятностью частица может быть обнаружена в различных точках пространства

Импульс частицы в любой точке пространства

Траекторию, по которой движется частица

Состояние микрочастицы в данном состоянии описывается волновой функцией, квадрат модуля которой определяет…

*Плотность вероятности нахождения микрочастицы в данном состоянии

Кинетическую энергию микрочастицы в данном состоянии

Потенциальную энергию микрочастицы в данном состоянии

Вероятность нахождения микрочастицы в данном состоянии

Вероятность dP (x) обнаружения электрона вблизи точки с координатой x на участке dx равна…

*dP (x)= │Ψ(x)│² dx

dP (x)=Ψ(x²)· dx

dP (x)= Ψ²(x)· dx

dP (x)= Ψ(x)· dx

В стационарных состояниях, описываемых волновой функцией

,

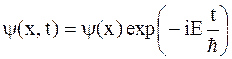плотность вероятности данного состояния…

*Не зависит от времени

Зависит от времени гармонически

Зависит от времени экспоненциально

Зависит от времени линейно

Уравнение Шрёдингера (конкретные ситуации)

Частица массой m с энергией E < U₀ подлетает к потенциальному барьеру высотой U₀ . Для области I уравнение Шредингера имеет вид…

*

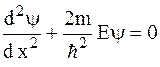
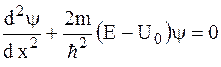
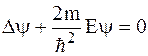
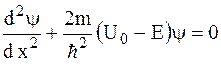
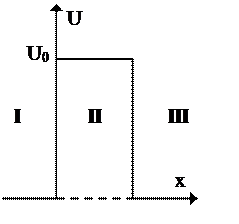
Частица массой m с энергией E < U₀ подлетает к потенциальному барьеру высотой U₀ . Для области II уравнение Шредингера имеет вид…

*

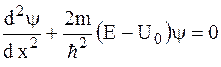
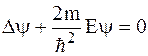
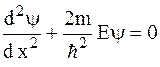
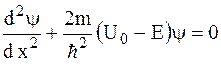
Стационарное уравнение Шредингера имеет вид

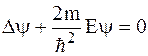
Это уравнение описывает движение …

*частицы в трехмерном бесконечно глубоком потенциальном ящике

частицы в одномерном бесконечно глубоком потенциальном ящике

линейного гармонического осциллятора

электрона в водородоподобном атоме

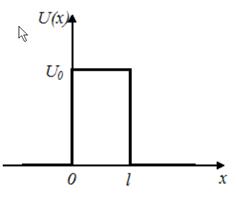
Квантовая и классическая частицы с энергией Е, движущиеся слева направо, встречают на своем пути потенциальный барьер высоты U₀ и ширины l.

Если P − вероятность преодоления барьера, то для …

*квантовой частицы при E < U₀ P ¹ 0, а при E > U₀ P < 1

классической частицы при E < U₀ P ¹ 0, а при E > U₀ P < 1

квантовой частицы при E < U₀ P = 0, а при E > U₀ P = 1

квантовой частицы P зависит только от U₀ и не зависит от l.

В результате туннельного эффекта вероятность прохождения частицей потенциального барьера увеличивается с …

*уменьшением массы частицы

увеличением ширины барьера

уменьшением энергии частицы

увеличением высоты барьера

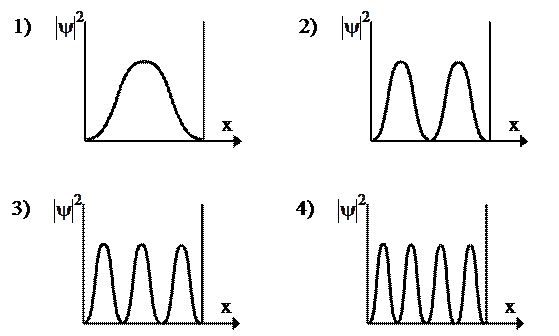На рисунке приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n = 2 соответствует график …

1) *2) 3) 4)

На рисунке приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n = 4 соответствует график …

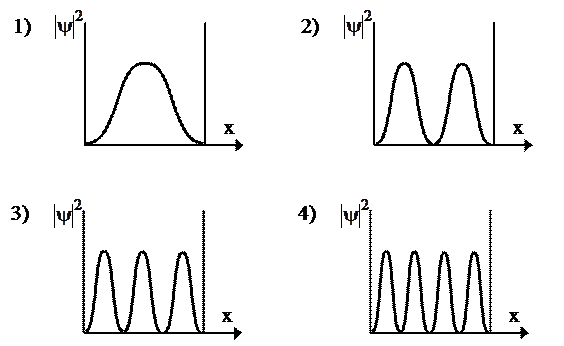1) 2) 3) *4)

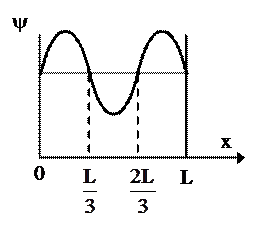Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

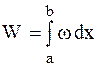где ω - плотность вероятности, определяемая ψ- функцией. Если ψ - функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке 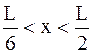равна …

*

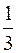
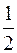
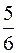
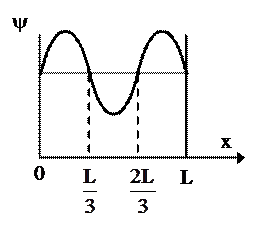Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

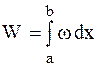где ω - плотность вероятности, определяемая ψ- функцией. Если ψ - функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке 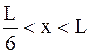равна …

*

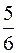
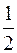
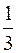
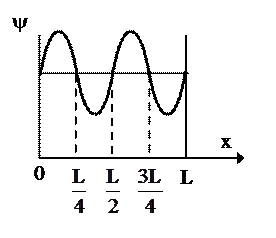Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

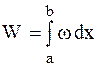где ω - плотность вероятности, определяемая ψ- функцией. Если ψ - функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке 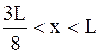равна …

*

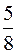
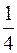
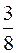
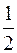
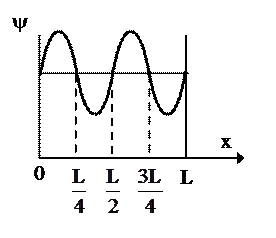Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

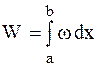где ω - плотность вероятности, определяемая ψ- функцией. Если ψ - функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке 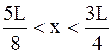равна …

*

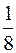
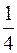
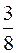
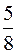
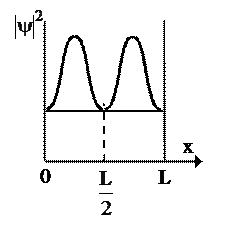На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность её обнаружения в центре ямы равна …

*0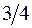

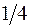
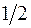
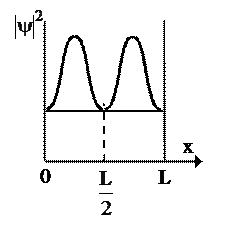На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность её обнаружения на участке 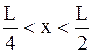равна …

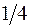
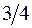* 0

На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n. В состоянии с n = 4 вероятность обнаружить электрон в интервале от 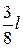до l равна

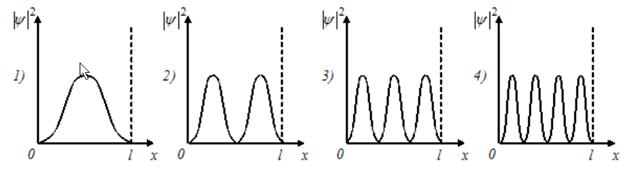
*5/8 3/8 3/4 7/8

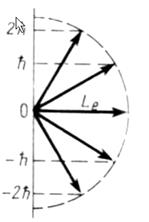
На рисунке приведены возможные ориентации вектора 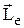– орбитального момента импульса электрона в атоме. Значение орбитального квантового числа для указанного состояния равно:

*2 1 4 5

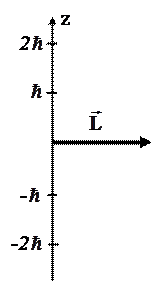
На рисунке приведена одна из возможных ориентаций момента импульса электрона в р-состоянии. Какие еще значения может принимать проекция момента импульса на направление Z внешнего магнитного поля?

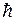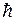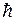- 2 *- * 2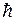

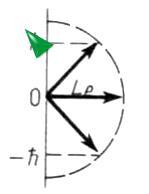
Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса 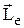электрона. На рисунке приведены возможные ориентации вектора 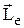. Значение орбитального квантового числа и минимальное значение главного квантового числа для указанного состояния соответственно равны …

*l = 1, n = 2

l = 1, n = 1

l = 3, n = 3

l = 3, n = 4

На рисунке приведены возможные ориентации вектора 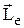. Величина орбитального момента импульса (в единицах ħ) для указанного состояния равна …

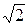
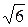* 2 3

На рисунке приведены возможные ориентации вектора 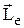. Величина орбитального момента импульса (в единицах ħ) для указанного состояния равна …

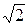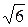* 2 3

Дата добавления: 2015-06-04